Potenciação de Matrizes
Produzido por Bruno PestanaTeoria
E aí, tudo bem? Se eu te der uma matriz e pedir pra você elevar ela à décima potência, como você faria?!
Matriz ao Quadrado
Vamos começar aprender Potência de Matriz do mais simples…bora ver como elevar uma matriz ao quadrado! Se liga nesse exemplo:
Essa continha é relativamente simples, ela funciona como uma multiplicação de matrizes normal, a única diferença é que você vai multiplicar a matriz por ela mesma!
Como Calcular a Potência de uma Matriz?
Agora vamos pegar a mesma matriz
Sim, essa conta é bem chatinha, principalmente se quiséssemos elevar uma matriz a um expoente grande! A boa notícia é que esse método funciona sempre!
Existe um outro método…que não vai funcionar sempre, mas quando funcionar vai facilitar MUITO a nossa vida! Bora conhecer?
📢 Clique para ver mais:
- Potência de Matriz: Exercícios Resolvidos
- Como diagonalizar uma matriz
- Autovalores e Autovetores de uma Matriz;
Potência de uma Matriz Simétrica
Esse método que eu vou te ensinar agora só vai funcionar pra matrizes simétricas. Em uma matriz simétrica a diagonal principal vai funcionar como uma espécie de espelho, saca só:
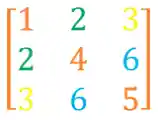
Entendeu o espirito da coisa?! Agora vamos ver como funciona esse truque, vamos pegar a nossa matriz
Você também pode conferir esse exemplo em vídeo:
Exemplo: Calcule
Vamos começar calculado as matrizes
Fazendo algumas contas achamos que os autovalores são
Ou seja, agora já sabemos os valores de
E agora ta tudo só no ponto de elevar!
Substituímos os valores:
Vamos efetuar potenciação da matriz :
E agora é só resolver as multiplicações matriciais:
E prontinho! Resolvido!