Seja Calcule
(a)
(b)
(c)
(d)
Passo 1
Queremos elevar uma matriz a um expoente real, então vamos precisar diagonalizar a matriz!
Ou seja, vamos ter que fazer:
Onde D é a matriz diagonal com autovalores na diagonal e P é a matriz com autovetores na coluna.
Lembrando que a ordem que os autovetores aparecem em P deve respeitar a ordem que os autovalores associados aparecem em D!
Agora vamos calcular os autovalores.
Passo 2
Para encontrar os autovalores de uma matriz, precisamos encontrar as raízes do polinômio característico:
Vamos ter então:
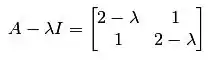
Para achar as raízes do polinômio característico, fazemos:
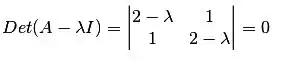
Daí tiramos que:
Passo 3
Agora usamos a definição de autovetor para achar os autoespaços associados a cada autovalor.
Para :
Temos o sistema:
As duas equações nos dão que:
Então um autovetor associado a é:
Fazendo a mesma coisa para :
Temos o sistema:
Agora as duas equações nos dão que:
Então um autovetor associado a é:
Passo 4
Agora já podemos diagonalizar a matriz A!
A matriz diagonal D vai ser:
Respeitando a ordem que os autovalores foram colocados, vamos ter a matriz P:
Calculando a inversa de P, vamos ter:
Agora, para elevar a matriz a 10, basta fazer:
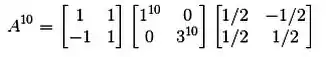
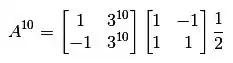
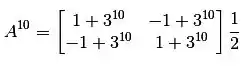
Agora vamos escrever isso de forma parecida com o que temos nas alternativas.
Separando os termos que têm expoente dos que não têm:
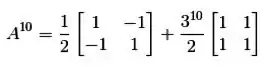
Resposta
(b)