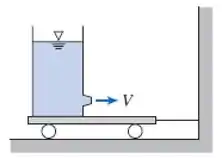
(Adaptada) Um grande tanque, de altura e diâmetro , está fixado sobre uma plataforma rolante conforme mostrado. Água jorra do tanque por meio de um bocal de diâmetro . A velocidade uniforme do líquido saindo do bocal é, aproximadamente, , em que y é a distância vertical do bocal até a superfície livre do líquido. Determine a tração no cabo para .
Passo 1
Para começar, vamos escolher o volume de controle (VC)?
Dentro do volume de controle, precisamos incluir o tanque (que sofre a ação a força de tração) e a saída de água pelo bocal (já que conhecemos sua velocidade!).
Esse VC está destacado em vermelho na figura abaixo:
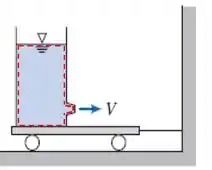
Passo 2
Show! Vamos então para o Passo 2: utilizar a equação de momento linear!
Vamos usar a equação para o eixo x, pois a velocidade imediatamente na saída do bocal encontra-se apenas nessa direção. Além disso, é no eixo x que está a tração, que é quem precisamos encontrar.
Outra vantagem de analisar a conservação do momento linear no eixo x: não tem outra força atuando nele. :D A força peso atua no eixo y.
Então vamos lá! Assumindo escoamento permanente, fluido incompressível, pressão atmosférica atuando de forma simétrica no tanque e propriedades uniformes, podemos usar essa equação:
No VC, não há uma vazão de entrada. Apenas saída.
Sabemos que a velocidade na saída em x é . Além disso, a tração T é a única força atuando nesse eixo:
Tá faltando encontrar essa vazão mássica. Para isso, podemos dizer que no fluido incompressível:
E a vazão volumétrica, por sua vez, é , então:
A área de saída é a área do bocal circular de diâmetro . Convertendo para o sistema internacional:
Voltando na equação do momento linear
Como
O enunciado pede a Tração quando , logo: