(Adaptado) Você foi requisitado para efetuar um estudo de viabilidade do projeto de um aquecedor de sangue para ser usado durante processos de transfusão de sangue. Esse trocador deve aquecer o sangue oriundo do banco de sangue de a ,a uma vazão de .
O sangue passa através de um tubo com seção transfusão retangular; por ; formado entre duas placas que são mantidas a uma temperatura constante de .
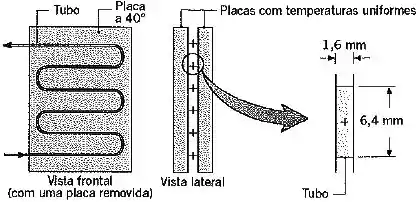
Calcule o comprimento de tubo necessário para atingir as condições de saída desejadas com a vazão especificada. Considere o escoamento plenamente desenvolvido e que o sangue possua as mesmas propriedades da água.
Dado: Considere a taxa de transferência de calor dada por , onde e corresponde à área lateral do tubo.
Passo 1
Logo de cara precisamos determinar as propriedades da água, para isso, usaremos a média das temperaturas de entrada e saída, dadas por:
De acordo com a tabela A.6 do Incropera, para as propriedades da água líquida, temos que:
Passo 2
Podemos encontrar o comprimento adequado para o tubo utilizando a expressão para a taxa de transferência de calor, dada por:
Onde , sendo o perímetro da seção transversal. Dessa forma:
Dessa equação, precisamos calcular o coeficiente convectivo, então vamos atrás dele.
Passo 3
Para encontrar o coeficiente convectivo, precisamos do número de Reynolds, dado por:
Onde o diâmetro hidráulico é dado por:
Além disso, a velocidade é dada por:
Onde:
Logo:
Finalmente, o número de Reynolds será:
Como o escoamento é laminar, considerando o mesmo totalmente desenvolvido, com temperatura superficial constante e razão , temos que o número de Nusselt será:
Assim, o coeficiente convectivo será:
Passo 4
Voltando à expressão de , temos:
Onde:
Finalmente:
![]()