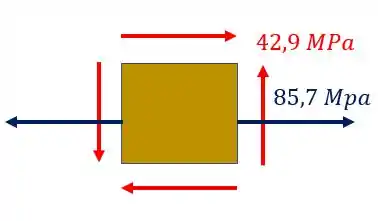
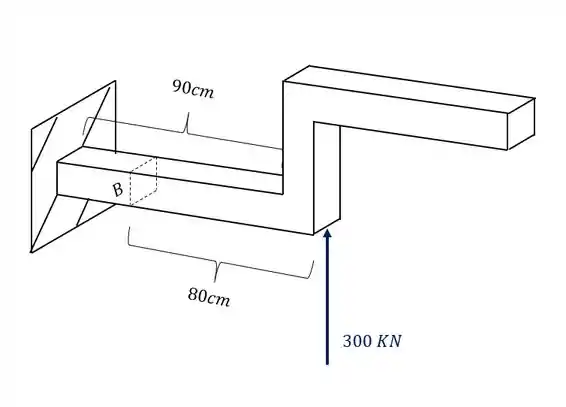
A barra de aço retangular abaixo, de base 30mm e altura 70mm, foi sujeita ao carregamento mostrado na figura. Determine o estado plano de tensões que ocorrem no ponto B da nossa barra.
Passo 1
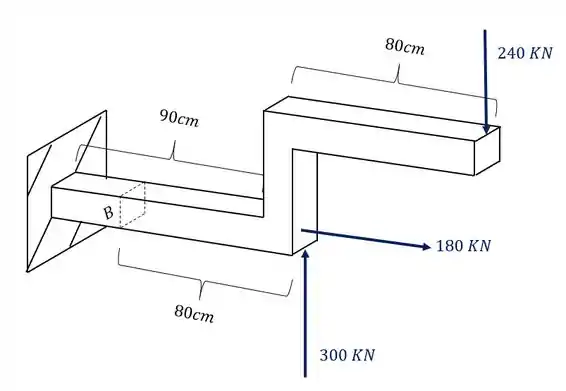
Para começar essa questão, devemos nos lembrar do nosso passo a passo. Devemos primeiro levar todos os esforços produzidos pelas cargas para a seção que se deseja calcular e analisar como esses esforços afetam o ponto B.
Analisando primeiro a carga de 240KN que vemos que ela produz uma força cortante, também um esforço fletor como mostra a figura abaixo.
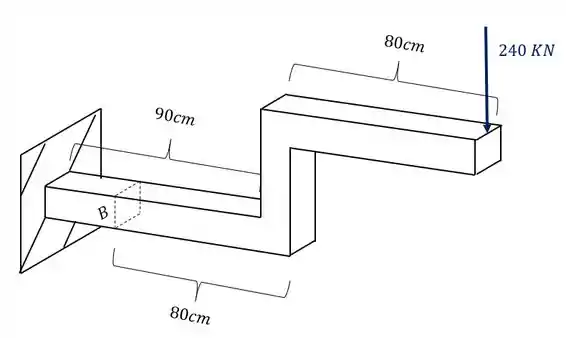
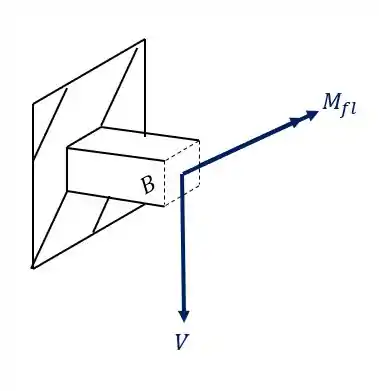
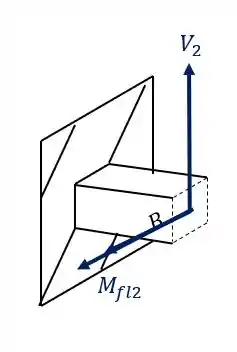
podemos ver também que a carga de 300 KN produz uma componente cortante e também um momento fletor
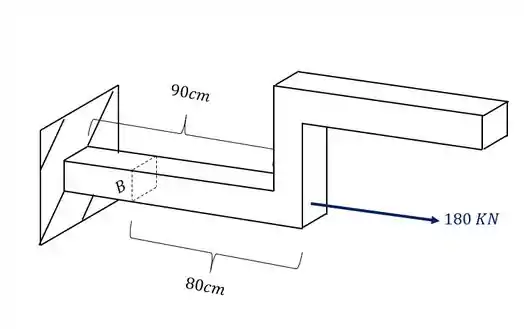
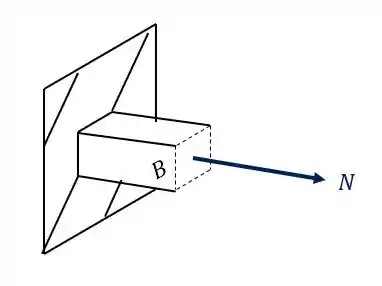
Além disso podemos ver que a carga de 180 KN produz na nossa seção apenas uma componente, que nesse caso é uma força normal, como podemos ver na nossa figura
Analisando a nossa seção com todos os esforços juntos teremos que
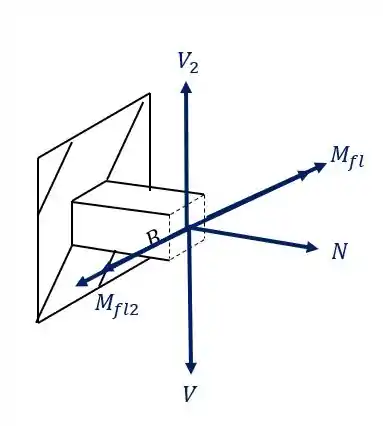
Nesse caso tanto o cortante quanto o momento fletor são diferentes, logo, precisamos usar características diferentes já que ambos os valores são diferentes.
Passo 2
Agora que já descobrimos os esforços que aparecem, precisamos calcula-los. Já sabemos de antemão que a força normal produz esforços normais, assim como o momento fletor. Da mesma forma força cortante produz esforços cisalhantes assim como o torsor. Então vamos dividir essa segunda parte da solução em duas partes.
Primeiro vamos calcular os esforços normais devido a ação da força normal.
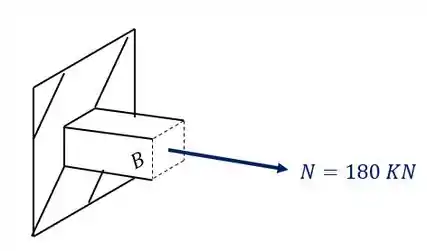
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que o normal será dado por
E a área será dada por
Substituindo na fórmula principal teremos que
Olhando novamente a figura, vemos que nosso elemento é
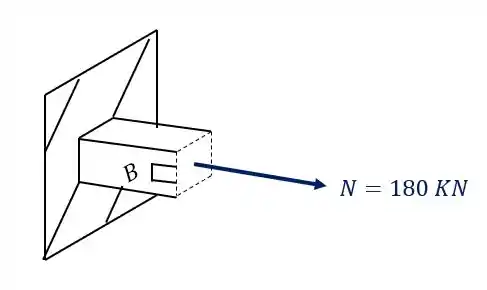
O nosso elemento isolado com a tensão será
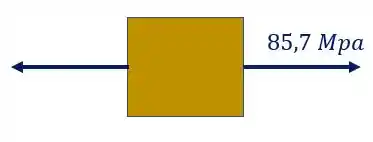
É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento.
Passo 3
Vamos calcular os esforços normais devido a ação do momento fletor. Mas perceba o seguinte, devemos primeiro calcular o momento devido a carga de 240 KN e depois a causada pela carga de 300 KN, e fazer o cálculo para a carga resultante. Com isso teremos que, primeiro
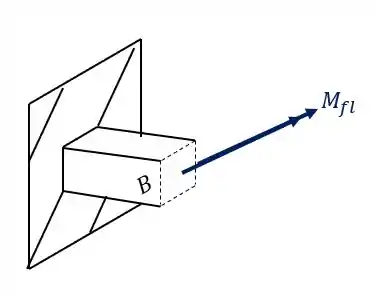
Como esse momento fletor é causado pela carga de 240 KN, devemos fazer o valor da carga vezes o braço de alavanca, com isso teremos que
Também sabemos que há um momento fletor na outra direção, que na nossa figura é dada por
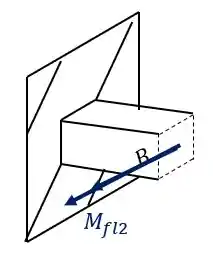
Como esse momento fletor é causado pela carga de 300 KN, devemos fazer o valor da carga vezes o braço de alavanca, com isso teremos que
Logo o nosso momento fletor resultante será
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que y é a distância do centro da peça até o ponto calculado, como esse ponto está em cima da linha neutra, sabemos que seu valor é zero, logo
Se substituirmos isso na nossa equação teremos que
Ou seja, os esforços fletores não interferiram no nosso cálculo. Mas isso não significa que os esforços normais são zero, além do mais temos a carga de 180 KN que traciona a nossa seção, apenas podemos afirmar que para o ponto B a contribuição do momento fletor é zero.
Passo 4
Agora vamos fazer a análise por esforços cisalhantes.
Vamos primeiro analisar o cisalhante. Sabemos que a fórmula que nos auxilia no cálculo é a fórmula
Mas vamos olhar a nossa figura. Lembre-se que os nossos cortantes são diferentes, assim teremos que para o primeiro cortante teremos que
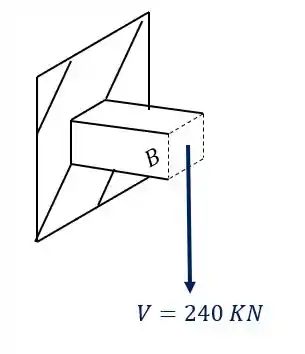
E para o segundo teremos que
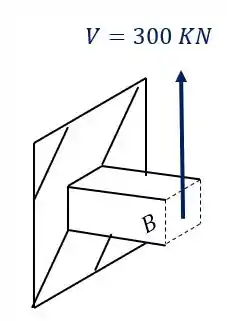
Logo o nosso cortante resultante será
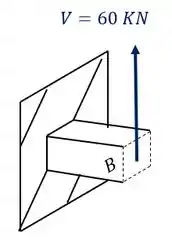
Logo o cortante que usaremos será
Também precisamos do momento estático da nossa seção, que é calculado por
Olhando a nossa seção teremos que
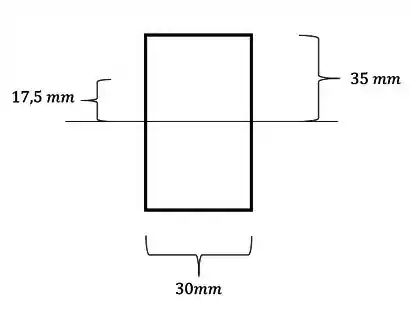
logo teremos que
Se olharmos a nossa fórmula vemos que também precisamos do valor do b, que é a espessura da nossa seção, e também já sabemos esse valor
E por fim precisamos do momento de inercia, como a seção é retangular usamos a fórmula
Como já temos as dimensões da seção, basta substituirmos esses valores
Agora que já temos os valores, basta substituirmos na nossa equação
Substituindo na nossa equação teremos que
Olhando a nossa peça teremos que
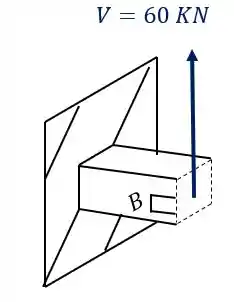
Com isso teremos que
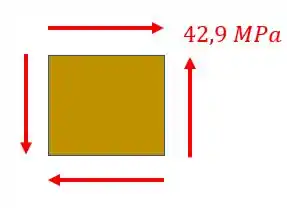
Passo 5
Por fim basta fazermos o elemento final com todos os esforços que representamos anteriormente, tendo dessa maneira o seguinte elemento para representarmos.