De quantas formas 4 pessoas podem se sentar ao redor de uma mesa circular?
Solução
Quando elementos são dispostos ao redor de um círculo; a cada disposição possível chamamos permutação circular. Além disso, duas permutações circulares são consideradas idênticas se, e somente se, quando percorremos a circunferência no sentido anti-horário a partir de um mesmo elemento das duas permutações, encontramos elementos que formam sequências iguais. Por exemplo, consideremos as permutações circulares:
- Tomando o elemento
, a sequência encontrada é (
).
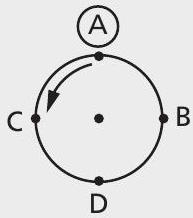
- Tomando o elemento
, a sequência encontrada é (A, C, D, B).
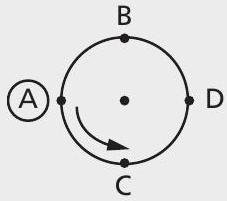
Logo, as duas permutações circulares são iguais. A igualdade das duas permutações circulares acima poderia ser observada, tomando-se outro elemento diferente de A. Por exemplo, D. Em (1) encontraremos a sequência (D, B, A, C) e em (2) encontraremos a sequência (D, B, A, C). Para resolvermos o exercício proposto, chamemos de x o número de permutações circulares. Notemos que a cada permutação circular de A, B, C, D correspondem 4 permutações de A, B, C, D.
Por exemplo: as permutações circulares do exemplo correspondem às permutações:
(A, C, D, B)
(D, B, A, C)
(C, D, B, A)
(B, A, C, D)
Por outro lado, no conjunto das permutações, a cada quatro permutações corresponde uma única permutação circular. Por exemplo:
(A, B, D, C)
(D, C, A, B)
(B, D, C, A)
(C, A, B, D)
correspondem a permutação circular:
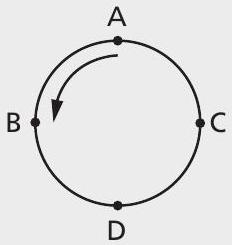
A cada conjunto de 4 permutações que definem uma determinada permutação circular chamamos de classe.
Como temos x permutações circulares, teremos x classes.
Observemos que a interseção de duas classes distintas é o conjunto vazio. Logo, o número de permutações de A, B, C, D pode ser calculado de dois modos:
19)
!
2?) existem
classes, cada qual com 4 permutações; logo, o total de permutações é
.
Portanto:
Observação:
Com raciocínio análogo ao anterior, podemos calcular o número de permutações circulares de
elementos, da seguinte forma:
- existem
! permutações dos
elementos;
- existem
permutações circulares em que a cada uma correspondem
permutações.
Logo:
que é o número de permutações circulares de
elementos.