Desempenho de Aletas
Teoria
Eficiência da Aleta
A taxa máxima na qual uma aleta poderia perder calor por convecção é aquela que ocorreria se a toda a aleta estivesse na temperatura da base . Nesse caso:
Onde é a área de troca térmica da aleta (área da extremidade e das laterais).
Mas como a temperatura da aleta vai diminuindo da base até sua extremidade, a quantidade de calor trocada é menor que . Então, a gente pode escrever que a taxa real de calor é dada por:
Em que é a eficiência da aleta, um número entre e , que pode ser encarada como a razão entre a taxa de calor real () e a taxa de calor se toda a aleta estivesse na temperatura da base :
Eficácia ou Efetividade da Aleta
Além da eficiência, existe outro parâmetro também utilizado, que é a efeividade da aleta (). Ele é a razão entre a taxa de calor real da aleta por convecção () e a taxa de convecção que haveria se a superfície não tivesse aleta.
Em que é a área da seção transversal na base da aleta.
Maaaaaas, não podemos afirmar com convicção que a transferência de calor vai melhorar se colocarmos uma aleta.
A aleta também representa uma resistência térmica à transferência de calor na superfície original. Por isso não dá pra afirmar logo de cara que a taxa de transferência de calor vai aumentar. E esse é um dos motivos de usarmos a efetividade para fazer essa avaliação.
Resistência Térmica da Aleta
Como já falamos em resistência térmica, vamos um pouco além com esse conceito, ok? Por definição, a resistência térmica é a razão entre o gradiente de temperatura e a taxa de transferência de calor, logo:
Logo, a resistência térmica da aleta () é dada por:
Isso quer dizer que a gente pode calcular a resistência térmica pra determinar a taxa de calor da aleta.
Pra isso, a gente precisa determinar a eficiência da aleta. “Mas como?” Cada geometria de aleta tem uma eficiência diferente e existem basicamente duas formas de se calculá-la: por gráficos ou por equações.
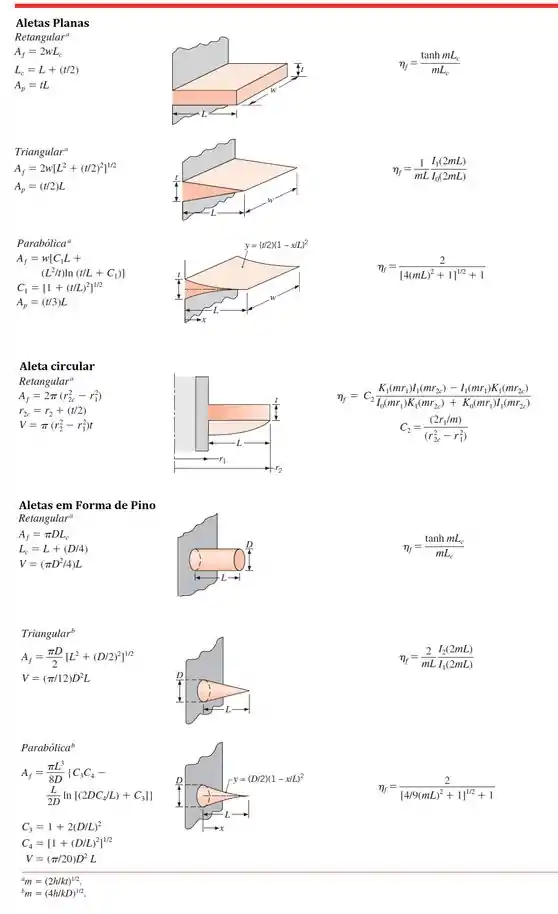
Os gráficos são mostrados aqui embaixo e a tabela com as equações está no fim desse conteúdo:
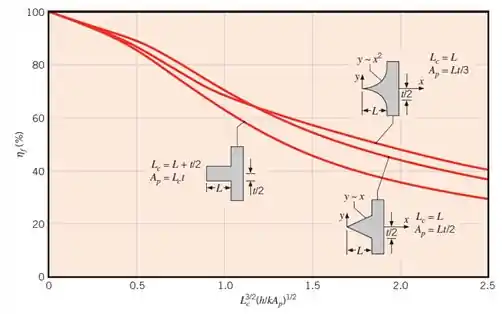
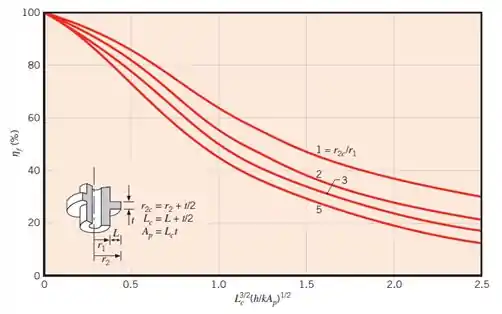
Para algumas das geometrias, você verá os termos comprimento corrigido () e raio corrigido (). Eles são uma estratégia, para que todos os casos possam ser tratados como tendo uma condição de contorno de extremidade adiabática.
“Mas como assim?” Uma aleta que troca calor simultaneamente pelas suas laterais e pela extremidade é igual a uma aleta que só troca calor pelas laterais, mas com uma área lateral um pouquinho maior.
Porque, afinal, a gente pode considerar a contribuição da área da extremidade como se fosse uma porção adicional da área lateral e isso facilita bastante a nossa vida.
Daí, esse comprimento ou raio que garante que a área lateral é grande o suficiente pra contabilizar a área da extremidade é o comprimento ou raio corrigido. Mas não se preocupa, que tem nos gráficos como calcular eles! ^^
Agora que a gente já virou os mestres das aletas, bora encarar os exercícios!
Eficácia ou Efetividade da Aleta ε a
Resistência Térmica da Aleta
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Aletas de alumínio () de perfil triangular são fixadas em uma parede cuja temperatura de superfície é . A base da aleta possui de espessura e seu comprimento é de . O sistema está no ar ambiente a temperatura de é o coeficiente de convecção de superfície é .
Quais são a eficiência e a efetividade da aleta?
Qual o calor dissipado por unidade de largura para uma única aleta?
Passo 1
Quais são a eficiência e a efetividade da aleta?
O enunciado propõe uma aleta triangular como mostrado aqui embaixo:
Para este tipo de geometria, a gente precisa tirar a eficiência no gráfico:
Pra isso, a gente precisa calcular o valor do eixo do gráfico ():
Em que:
Assim:
Pelo gráfico:
Logo:
Passo 2
Por definição, a efetividade e a eficiência de aletas são calculadas, respectivamente, por:
Então a gente pode relacionar as duas por meio da taxa :
Assim:
Passo 3
Vamos trabalhar nas áreas para calcular a efetividade da aleta. O termo é a área da aleta e é a área da seção transversal na base. Elas são dadas por:
Em que pode ser entendido pela imagem abaixo:
Logo:
Dividindo pela largura , a gente fica com a área por unidade de comprimento:
Além disso, a área da base por unidade de comprimento será:
Dessa maneira, a efetividade será:
Passo 4
Qual o calor dissipado por unidade de largura para uma única aleta?
A taxa de calor por unidade de largura pode ser calculada tanto pela eficiência quanto pela efetividade, dado que a gente já sabe as duas!
Vou escolher usar a efetividade, mas tanto faz, tá bem? :) Pela definição:
Logo:
Dividindo pela largura da aleta () em ambos os lados, ficamos com:
Substituindo os valores do enunciado:
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Uma barra de diâmetro e condutividade térmica se projeta na direção normal, a partir de uma parede de uma fornalha que está a uma temperatura e é coberta com um isolamento de espessura . A barra é soldada à parede da fornalha e é utilizada como um gancho para suporte de cabos de instrumentação. Para evitar danos aos cabos, a temperatura da barra em sua superfície exposta () deve ser mantida abaixo do limite de operação especificado de . A temperatura do ar ambiente é é o coeficiente de convecção,.
Calcule a temperatura da superfície exposta em função dos parâmetros térmicos e geométricos dados. A barra possui um comprimento exposto de e sua extremidade é bem isolada. Verifique se a temperatura ultrapassa o limite.
Passo 1
Antes de partir pros cálculos, bora entender a situação? No problema, a gente tem uma aleta de seção uniforme circular, em que parte dela está isolada e parte dela pode trocar calor. Além disso, sua extremidade também está isolada!
Como o forno é a região mais quente da situação, esperamos que o fluxo saia de sua parede em sentido do ar ambiente.
Mas, como a parte inicial da aleta está isolada, a energia é transportada somente por condução incialmente ao longo da aleta e, depois, ela passa a ser transportada por condução até o final, mas também é liberada por convecção para o ambiente na região sem isolamento. Entendido?
Bom, no problema, a temperatura de toda a barra não deve ultrapassar os . Mas se a gente garantir que a temperatura logo após o isolamento é menor que , então garantimos que toda a barra estará numa temperatura menor que .
Isso acontece porque ao longo da barra, ela troca calor com o ambiente e a temperatura vai diminuindo.
Passo 2
Beleza! Entendido o problema, a gente pode então usar nossa estratégia de montar o circuito térmico pra achar a temperatura :
Como a taxa é constante ao longo de todo o circuito, a gente tem duas formas de se fazer a questão pelo menos:
I) Por meio das equações analíticas da taxa de calor de aletas
A gente sabe que a taxa de calor que passa por uma aleta de seção uniforme com extremidade adiabática (caso ) é dada por:
Em que:
Como a taxa é constante, a gente pode escrever que:
Substituindo a expressão de :
Nessa equação, a única incógnita é a temperatura e a gente consegue resolver!
Passo 3
A segunda forma de fazer a questão é:
II) Por meio dos gráficos de eficiência.
Se a taxa é constante, então a taxa de calor que passa pelo trecho isolado é igual à taxa que passa por todo o sistema:
Isolando a temperatura na equação, a gente fica com:
Em que as temperaturas e são conhecidas e as resistências são calculadas por:
E, assim, a gente pode calcular cada uma das resistências pra determinar a temperatura . Daí pra calcular a , a gente precisaria da eficiência (), que é obtida por um dos gráficos que vimos na teoria!
Passo 4
Aqui vou fazer com vocês a resolução pela equação analítica, que é sempre mais preciso usar equações do que gráficos! Recapitulando, a gente descobriu a seguinte equação:
Então, bora calcular o que dá pra calcular, como: o perímetro , o valor de e a resistência por condução .
O perímetro é dado por:
E o valor de é dado abaixo:
Em que a área é a área transversal da aleta, ou seja, a área de um círculo como diâmetro ! Sendo assim:
Agora, a gente pode calcular a resistência de condução:
Substituindo os valores:
Passo 5
Pronto! Substituindo todos os valores conhecidos, ficamos com:
Em que, o valor de será:
Dessa maneira, substituindo na equação:
Reorganizando a equação:
Isolando a temperatura:
Isso equivale a cerca de . Logo, a temperatura vai ultrapassar o limite estabelecido de .
Resposta
A temperatura equivale, em graus Celsius, a . Logo, a temperatura vai ultrapassar o limite estabelecido de .
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Tubos de aço utilizados no transporte de água pressurizada são unidos por flanges de espessura . Os diâmetros interno e externo dos tubos são e , respectivamente, e o diâmetro externo dos flanges é .
Em condições normais de operação, a superfície interna do tubo encontra-se a uma temperatura de , enquanto o ar ambiente está a . Se o coeficiente de convecção nas superfícies dos flanges é , qual a perda de calor através dos flanges? Considere a condutividade térmica do tubo e do flange iguais a.
Passo 1
Pra achar a taxa de calor que é perdida pelo sistema, bora dar uma olhadinha na vista lateral do desenho aqui embaixo:
O que tá acontecendo nesse problema? A superfície mais interna do sistema está bem quente () e tem um fluido a temperatura ambiente do lado de fora (). Dessa forma, a gente espera que haja um fluxo de calor de dentro pra fora.
A presença dos flanges acaba tendo a função de uma aleta, pois aumenta a área de troca térmica para o ambiente externo. Então, é só a gente fazer usar as fórmulas de aletas! ^^
Já que não há geração em nenhum dos materiais, a gente pode usar a estratégia do circuito térmico! Ficaria da seguinte maneira:
Então, a taxa de calor pode ser escrita em função das resistências:
Em que as resistências térmicas de condução na parede cilíndrica () e no flange () são calculadas por:
Passo 2
Bora calcular as resistências! Primeiro com a que a gente já tá mais acostumado:
- Resistência térmica de condução na parede cilíndrica:
- Resistência térmica de uma aleta anular simples (flange):
Substituindo os valores do enunciado:
Passo 3
Agora, vamos à resistência que mais interessa:
Da expressão aqui em cima, a gente só sabe o coeficiente , mas precisamos determinar a área () e eficiência da aleta ().
A área da aleta é essa área aqui em vermelho:
Então, a gente pode escrever que:
Mas a gente pode usar aquela estratégia do raio corrigido (), que é quando a gente assume que a contribuição da área lateral é adicionada à área do disco. Sendo assim:
Em que:
Substituindo os valores do enunciado:
Passo 3
Agora só falta a eficiência ()! Pra calcular a eficiência desse formato de aleta (anular), a gente tem que utilizar o gráfico que já vimos:
Para determinar a eficiência, a gente precisa então saber qual das quatro curvas representa a nossa aleta e calcular com o valor desse eixo aí loucão. Então, bora lá!
Bora calcular o valor de x do gráfico:
Em que e são calculados pelas expressões mostradas no gráfico:
Além disso:
Ufa! Agora a gente pode finalmente calcular o valor de x:
Pra saber qual das curvas serve pra gente, precisamos calcular a razão entre os raios:
Agora vamos voltar para o gráfico.
Passo 4
Não tem nenhuma curva com o valor que encontramos, mas a gente pode colocar mais ou menos entre as curvas de razão igual a e , um pouco mais próximo da curva de .
Agora a gente já pode marca no gráfico a posição da abscissa e ver a eficiência correspondente:
Concluimos, assim, que:
Passo 5
Com a área e eficiência calculadas, a gente pode finalmente determinar a resistência térmica da aleta:
Logo:
Passo 6
Prontinho! Agora ficou fácil calcular a taxa de calor:
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptada) A intensidade na qual a condição na extremidade afeta o desempenho térmico de uma aleta depende da geometria da aleta e de sua condutividade térmica, assim como do coeficiente convectivo.
Considere uma aleta retangular de uma liga de alumínio , com comprimento , espessura e largura .
A temperatura da base da aleta é e ela está exposta a uma fluido com temperatura .
Supondo um coeficiente convectivo uniforme sobre toda a superfície da aleta, determine a taxa de transferência de calor na aleta por unidade de largura , a eficiência , a efetividade , a resistência térmica por unidade de largura e a temperatura da extremidade para os Casos , da tabela abaixo.
Contraste os resultados com aqueles para aproximação de aleta infinita.
Passo 1
Show de bola! O problema está pedindo pra calcularmos algumas coisas, certo? Então vamos organizar todas as equações que precisamos aqui, beleza?
Onde é a transferência de calor na aleta por unidade de largura.
O nosso trabalho então vai ser, para cada caso, determinar (pela tabela) e calcular o restante dos valores, beleza?
Passo 2
Antes de continuarmos, vamos nos antecipar aqui e calcular logo alguns parâmetros que vão aparecer nos próximos passos.
Onde e , logo:
Para :
Agora estamos prontos pra seguir em frente!
Passo 3
Caso A
Pela tabela:
Nesse caso, também precisamos calcular a temperatura da aleta quando . Então, partindo de:
Simplificando, pois :
Substituindo :
Substituindo demais valores:
Passo 4
Caso B
Pela tabela:
Nesse caso, também precisamos calcular a temperatura da aleta quando . Então, partindo de:
Substituindo:
Passo 5
Caso D
Pela tabela:
No caso de uma aleta infinita, , logo:
Para aleta infinita, pela tabela, . Dessa forma,
Resposta
Caso A
Caso B
Caso D
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
(Adaptada) Uma aleta plana fabricada com a liga de alumínio 2024 tem uma espessura na base de e um comprimento de .
Sua temperatura na base é de e ela está exposta a um fluido para o qual e .
Para as condições anteriores e uma aleta de largura , compare a taxa de transferência de calor na aleta e a eficiência para os perfis retangular e parabólico.
Passo 1
Por definição, a eficiência da aleta é dada por:
Assim, a taxa de transferência de calor será:
Um detalhe importante aqui é que, como , o que vamos calcular aqui é a taxa de transferência de calor por unidade de largura, logo:
A ideia aqui vai ser a seguinte, para cada caso (perfil retangular e perfil parabólico), vamos calcular e .
Passo 2
Perfil retangular
Nesse caso:
Onde:
Como e , logo:
Logo:
Passo 3
Para o perfil retangular, a taxa de transferência de calor por unidade de largura será:
Onde:
Logo:
Passo 4
Perfil parabólico
Nesse caso, a eficiência da aleta é dada por:
A taxa de transferência de calor nesse caso será dada por:
Onde:
Voltando para a expressão da taxa de transferência de calor:
Resposta
Perfil retangular
Perfil parabólico
Exercício Resolvido #6
ÇENGEL, Y. A. Heat Transfer: A Practical Approach
(Adaptada) Uma superfície quente a deve ser resfriada fixando-se aletas de alumínio de de comprimento e de diâmetro. A temperatura ambiente é de e o coeficiente de transferência de calor nas superfícies é de .
Determine a taxa de transferência de calor da superfície de cada aleta. Também determine a eficácia de cada aleta.
Passo 1
A taxa de transferência de calor da superfície da aleta é dada por:
Então precisamos começar calculando a sua eficiência . Olhando na tabela na Teoria desse tópico (e provavelmente no seu livro também). Vemos que:
Sendo , onde:
Substituindo os valores:
Dessa forma, a eficiência da aleta será:
Passo 2
A área de troca da aleta é dada por:
Substituindo os valores:
Passo 3
Finalmente, a taxa de transferência de calor será:
Substituindo os valores:
Passo 4
A eficácia da aleta é dada por:
Em que é a área da seção transversal na base da aleta, logo:
Substituindo os valores:
Resposta
Exercício Resolvido #7
ÇENGEL, Y. A. Heat Transfer: A Practical Approach
Dois tubos de vapor de ferro fundido de de comprimento e de espessura com um diâmetro exterior de estão ligados um ao outro através de dois flanges de de espessura com um diâmetro exterior de .
O vapor flui dentro do tubo a uma temperatura média de com um coeficiente de transferência de calor de . A superfície externa do tubo é exposta a um ambiente a , com um coeficiente de transferência de calor de .
Desconsiderando os flanges, determine a temperatura média da superfície externa do tubo.
Usando esta temperatura para a base do flange e tratando os flanges como as aletas, determine a eficiência da aleta e a taxa de transferência de calor dos flanges.
Qual comprimento de tubo é a seção de flange equivalente a para fins de transferência de calor?
Passo 1
Desconsiderando os flanges, determine a temperatura média da superfície externa do tubo.
O circuito térmico que representa o drama aqui é o seguinte:
Onde e são as resistências térmicas de convecção nas superfícies interna e externa respectivamente.
“Qual é a ideia aqui?!”
Podemos calcular a temperatura na superfície interna da seguinte forma:
Mas nós ainda não temos a taxa de transferência de calor . Mas podemos calculá-la utilizando a resistência térmica total do sistema:
Show de bola! Vamos fazer isso então!
Passo 2
Vamos começar pelas resistências térmicas, ok?
- Resistência térmica de convecção na superfície interna:
- Resistência térmica de condução:
- Resistência térmica de convecção na superfície externa:
Como estamos trabalhando com um cilindro, a resistência térmica de condução será:
Como temos três resistências térmicas em série, a resistência térmica total será:
Passo 3
Agora podemos calcular a taxa de transferência de calor no sistema:
Substituindo os valores:
Passo 4
Já podemos calcular a temperatura na superfície externa agora.
Passo 5
Usando esta temperatura para a base do flange e tratando os flanges como as aletas, determine a eficiência da aleta e a taxa de transferência de calor dos flanges.
A eficiência da aleta pode ser calculada através do gráfico abaixo:
Para isso, precisamos dos seguintes valores:
Onde:
Substituindo todos os valores:
Utilizando esses dados no gráfico, encontraremos:
Passo 6
A taxa de transferência de calor através do flange será dada por:
Onde:
Logo, a taxa de transferência de calor será:
Passo 7
Qual comprimento de tubo é equivalente à seção de flange para fins de transferência de calor?
O tubo de 6 metros transfere calor a uma taxa de:
Logo, por metro, essa taxa de transferência de calor passa a ser:
Sabendo que o flange transfere calor a uma taxa de , o comprimento equivalente será:
Resposta
Exercício Resolvido #8
Questão 1, UFF, P1-2017.2
Suponha que você tenha uma escolha entre uma aleta retangular e uma aleta de perfil triangular construída de alumínio puro (propriedades à ), ambos com uma espessura na base de . A profundidade da aleta é de .
O coeficiente convectivo é de e a temperatura do meio é de enquanto a base da aleta está a .
A aleta retangular possui de altura e a aleta de perfil triangular possui de altura. Qual dessas terá a melhor relação (mais favorável em termos térmicos) de taxa de transferência de calor por peso de material para compor a aleta?
Passo 1
Antes de qualquer coisa, vamos buscar as propriedades do alumínio a . De acordo com a tabela A.1 do Incropera:
Agora podemos seguir em frente.
Passo 2
Vamos começar tratando da aleta retangular. Como a área transversal é constante na aleta, podemos usar as soluções tabeladas.
Como temos um caso onde há convecção na extremidade, a taxa de transferência de calor na aleta é dada por:
Onde:
Logo:
Finalmente:
Passo 3
O peso da aleta retangular é dada por:
Assim, para a aleta retangular, a relação e taxa de transferência de calor por peso de material é dada por:
Passo 4
Para a aleta triangular, não podemos usar uma equação tabelada porque a área de seção transversal não é constante. Então vamos calcular a taxa de transferência de calor usando a sua eficiência, dada por:
Para este tipo de geometria, a gente precisa tirar a eficiência no gráfico:
Pra isso, a gente precisa calcular o valor do eixo do gráfico ():
Em que:
Assim:
Pelo gráfico:
Passo 5
A área total de troca térmica da aleta triangular é dada por:
Assim, a taxa de transferência de calor será:
Passo 6
O peso da aleta triangular será:
Assim, para a aleta triangular, a relação de taxa de transferência de calor por peso de material é dada por:
Comparando as duas aletas, a aleta retangular apresenta uma melhor relação de taxa de transferência de calor por peso de material.
Resposta
Aleta retangular:
Aleta triangular:
Exercício Resolvido #9
Questão 4, PUCRIO, P1-2005
A distribuição de temperaturas numa aleta muito longa de seção retangular (altura igual a , largura igual a e comprimento igual a ), em contato com o ambiente é dada por:
Determine a eficiência desta aleta, considerando que a condutividade térmica é igual a .
Passo 1
A eficiência da aleta é dada por:
Dessa equação, não sabemos nem o coeficiente convectivo, nem a taxa de transferência de calor.
Como a aleta é considerada muito longa, podemos utilizar a equação tabelada para a distribuição de temperatura na aleta, que é dada por:
Reorganizando a equação, teremos:
Opa! Comparando essa equação com a equação que o problema nos deu:
Podemos concluir que:
Passo 2
Sabendo o valor de , podemos calcular o coeficiente convectivo a partir da seguinte equação:
Passo 3
Como temos uma aleta longa, a taxa de transferência de calor da mesma é dada pela seguinte equação tabelada:
Passo 4
Assim, a eficiência da aleta será:
Onde é a área total de troca térmica, dada por:
Logo:
Resposta
Exercício Resolvido #10
Questão 3, UFF, P1-2016.1
(Adaptado) Qual a taxa de calor trocada por um aleta de pino de perfil retangular assumindo que essa seja feita de cobre (propriedades constantes dada pelos valores a ) seja de de altura, de diâmetro de base, que a temperatura da base seja de e que o coeficiente de película do ambiente seja e a temperatura do ambiente seja .
Passo 1
Antes de qualquer coisa, precisamos da condutividade térmica do cobre. De acordo com a tabela A.1 do Incropera, para o cobre puro:
Passo 2
A taxa de transferência de calor será dada por:
Onde é a efetividade da aleta, é o coeficiente convectivo, é a área lateral da aleta e é a diferença entre as temperaturas da base e do ar.
Dessa equação, precisamos calcular a efetividade e a área superficial da aleta.
Passo 3
A efetividade e a área superficial da aleta são calculadas por equações tabeladas, se liga:
Onde . Assim:
Assim, a eficiência da aleta será:
A area lateral da aleta será:
Passo 4
A taxa de transferência de calor será:
Resposta
Exercício Resolvido #11
Questão 4, UFRJ, P1-2008.1
Dois tubos de ferro fundido são unidos por flanges de ferro fundido, conforme mostrado abaixo.
O diâmetro interno do tubo é e seu diâmetro externo é de . O diâmetro externo da união flangeada é , com espessura de . Dentro do tubo escoa vapor a , com coeficiente de transferência de calor de .
O tubo e a união flangeada perdem calor para o ar a com coeficiente de transferência de calor de . No regime permanente e considerando-se perfeito contato entre os flanges:
Calcule a temperatura da superfície externa do tubo, sem a união flangeada;
Com o valor da temperatura externa do tubo calculado no item anterior, calcule a taxa de calor perdida para o ar pela união flangeada.
Calcule o comprimento de tubo necessário para transferir a mesma taxa dissipada através da união flangeada.
Passo 1
Calcule a temperatura da superfície externa do tubo, sem a união flangeada;
O circuito térmico que representa esse sistema é dado por:
Nesse caso, estamos interessados em calcular a temperatura . Pra isso, vamos precisar da taxa de transferência de calor, que pode ser calculada utilizando-se as resistências térmicas.
Onde é a resistência térmica total do sistema, dada por:
Assim, a taxa de transferência de calor será:
Para calcular a temperatura , vamos comparar esse valor com a taxa de transferência de calor entre a superfície da tubulação e o ar externo. Logo:
Passo 2
Com o valor da temperatura externa do tubo calculado no item anterior, calcule a taxa de calor perdida para o ar pela união flangeada.
Como a flange se trata de uma superfície aletada, podemos calcular a transferência de calor utilizando a sua eficiência da seguinte forma:
Onde:
A eficiência da aleta é dada através de um gráfico, onde:
Dessa forma, a taxa de transferência de calor será:
Passo 3
Calcule o comprimento de tubo necessário para transferir a mesma taxa dissipada através da união flangeada.
Nós encontramos no Passo 1 que:
Substituindo o valor de que encontramos, teremos:
Resposta