Conjunto de Aletas
Produzido por Giovanna RonzéTeoria
Introdução
A gente já viu como calcular eficiência, efetividade, resistência de uma aleta, certo? Mas, se elas são tão boas assim, por que a gente não coloca um monte de uma vez só?
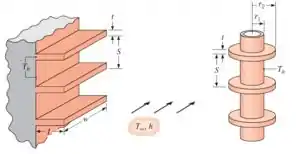
Pois é! Pensaram exatamente nisso! E daí que surgem as matrizes de aletas! Matriz é um conjunto de elementos, então isso significa que agora a gente vai trabalhar com várias aletas iguaizinhas numa dada superfície.
Mas não se preocupe! A transferência de calor vai aumentar com o número de aletas, mas nosso trabalho nos exercícios não vai aumentar tanto assim! Ahaha

Pelo que a gente viu antes, basicamente o que a gente faz pra calcular a taxa de calor é calcular a eficiência da aleta e a resistência dela. Aqui não vai ser diferente, mas as fórmulas se modificam um pouquinho. Então, dá uma olhadinha, grande mestre!
Então tem eficiência para matriz de aletas?
Tem sim, pequeno gafanhoto! E a definição é bem parecida, só que agora a gente tem várias aletas pra dar conta e não apenas uma! Dá uma olhadinha:
A taxa de calor total de um sistema com várias aletas () é dado pela convecção a partir das aletas () e da superfície primária sem aletas (), podendo ser expressa por
Na equação acima:
- : número de aletas;
- : eficiência da aleta;
- : coeficiente de transferência de calor por convecção;
- : área de troca térmica de uma aleta;
- : diferença de temperatura entre a base e o ambiente ;
- : área da porção exposta da base;
Agora que estamos todos familiarizados, podemos ir em frente!
Colocando o termo convectivo e a diferença de temperatura em evidência, temos:
A área da base exposta () pode ser expressa como:
Em que o termo é a área total do sistema, ou seja, é soma das áreas das aletas com a área da porção exposta da base.
Substituindo na expressão da taxa de calor total ():
Olha que bacana! A gente agora pode chamar esse termo dos colchetes de eficiência total do sistema aletado (), pra ficar com a mesma cara da taxa que achamos pra aletas simples:
A eficiência global da superfície () é a razão entre a taxa de calor real da aleta e a taxa de calor se a aleta estivesse toda na mesma temperatura que a base ().
Mas a fórmula que você precisa pra calcular é essa daqui:
Eu também posso usar resistência térmica aqui?
Circuitos térmicos ajudam a beça a gente, não é mesmo! Então, relaxa aí na cadeira que aqui também tá liberado usar resistências! Vamos ver que essa matriz grandona aí se reduz a uma única resistência , que descreve todo o sistema!

A gente já viu que a taxa total de calor é dada por:
Pela definição de resistência térmica (razão entre gradiente e taxa), a gente tem que:
Assim, temos a expressão para a resistência térmica total da matriz de aletas ():
Essa resistência representa toda a energia que é perdida pelo sistema (). Dá uma olhadinha só:
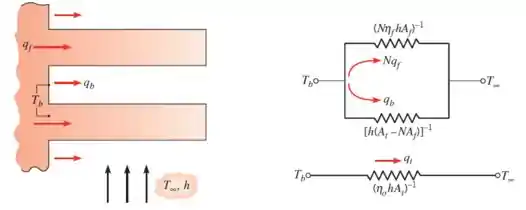
Na prática, você teria aquele circuito em paralelo ali pra resolver, mas com essa expressão, isso se resume a uma única resistência (circuito mais abaixo).
E se as aletas forem fabricadas e depois fixadas à parede?
Nesse caso, pode surgir uma resistência de contato () entre as superfícies. Então, a gente tem que saber cuidar desse caso também!
Mas como eu sou seu amigo, vou deixar tudo prontinho pra você só usar! Se liga aí nesse exemplo:
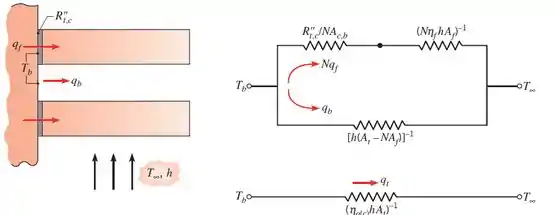
Com a resistência térmica de contato, aquele circuito em paralelo ficaria ainda mais chato, porque além de serem resistências em paralelo, existem duas resistências em série num dos ramos do circuito.
Mas, calma! Mais uma vez a gente pode simplificar tudo e esse “circuitão” aí se reduz a essa única resistência térmica:
A eficiência total com resistência de contato pode ser calculada por:
Em que:
OBS: Note que essa expressão é mais geral, porque se não tiver nenhuma resistência de contato (), a constante fica igual a e a expressão fica igual à anterior!
Agora estamos mais do que prontos pra cair dentro dos exercícios!
Eu também posso usar resistência térmica aqui?
E se as aletas forem fabricadas e depois fixadas à parede?
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
O motor cilíndrico de uma moto é constituído por alumínio () e tem uma altura de com diâmetro de . Sob condições normais de operação, a superfície externa do cilindro encontra-se a uma temperatura de e é exposta ao ar ambiente, cuja temperatura vale e cujo coeficiente de convecção é . Aletas anulares são integradas ao corpo cilíndrico do motor para aumentar a transferência de calor para a vizinhança.
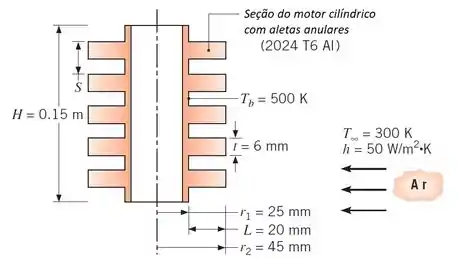
Considere cinco aletas anulares com espessura de , comprimento de e que estão igualmente espaçadas. Qual o aumento percentual na perda de calor ao utilizarmos as aletas?
Passo 1
Aqui a gente vai verificar se colocar aletas realmente é um bom negócio! Vem comigo então!
Caso não houvesse aletas, teríamos um cilindro trocando calor com o ambiente. Sendo assim, a taxa de calor seria calculada por:
A área do cilindro é dada por:
Sendo assim, a gente tem que:
Passo 2
Agora é a situação com as aletas! A taxa de calor trocada por um conjunto de aletas () é dada por:
Em que:
A área superficial de uma aleta anular é dada por:
A área total do sistema “aleta+base” é dada por:
Passo 3
Agora nos resta calcular o rendimento de uma aleta única (). Bora usar o gráfico (no capítulo anterior) pra isso:
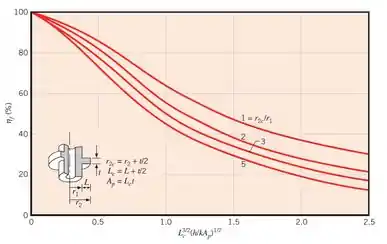
Então, a gente precisa calcular a razão entre e pra saber qual das quatro curvas usar e determinar o valor da abscissa!
Bora calcular o valor de x do gráfico então:
Em que e são calculados pelas expressões mostradas no gráfico:
Além disso:
Ufa! Agora a gente pode finalmente calcular o valor de x:
Pra saber qual das curvas serve pra gente, precisamos calcular a razão entre os raios:
Não tem nenhuma curva com esse valor, mas a gente pode colocar mais ou menos entre as curvas de razão igual a e , um pouco mais próximo da curva de .
Agora a gente já pode marca no gráfico a posição da abscissa e ver que a eficiência da aleta é aproximadamente:
Passo 4
Dessa maneira, é possível calcular a eficiência do sistema aletado e consequentemente a taxa de calor:
Substituindo os valores do enunciado:
Passo 5
Com as duas taxas calculadas a gente pode determinar o aumento percentual na perda e calor ao usarmos o sistema de aletas:
Esse valor é realmente relevante! Acho que ficou provado que as aletas ajudam bastante na troca de calor, não é mesmo?
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Como mais e mais componentes são colocados em um circuito integrado individual (chip), a quantidade de calor que é disputado tende a aumentar. Por outro lado, esse aumento está limitado pela temperatura máxima permitida de operação do chip, que é aproximadamente . Para maximizar a dissipação de calor, propõe-se utilizar uma matrix de aletas de cobre () em forma de pino que podem ser fixadas através de processos metalúrgicos a superfície externa de um chip quadrado de de lado.
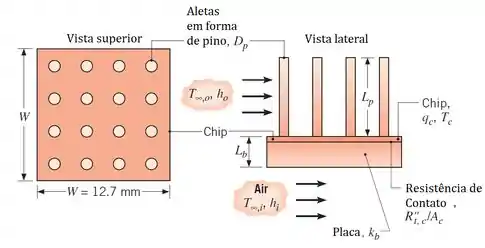
Condições: , , , e .
Esboce o circuito térmico equivalente para a montagem pino-placa, considerando condições de estado estacionário unidimensional e resistência de contato desprezível entro os pinos e o chip. Na forma de variáveis, enumere as resistências apropriadas, temperaturas e taxas de calor.
Para as condições prescritas anteriormente, qual é a máxima taxa na qual o calor pode ser dissipado no chip quando os pinos estão no lugar? Isto é, qual é o valor de para ? O diâmetro e o comprimento do pino são respectivamente e .
Passo 1
Esboce o circuito térmico equivalente para a montagem pino-placa, considerando condições de estado estacionário unidimensional e resistência de contato desprezível entro os pinos e o chip. Na forma de variáveis, enumere as resistências apropriadas, temperaturas e taxas de calor.
A situação pode ser ilustrada com esse esquema aqui embaixo:
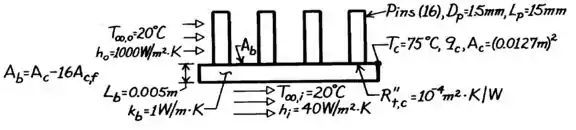
A gente sabe, pelo enunciado, que o calor que e gerado no chip será dissipado, tanto para a região externa quanto para a região interna.
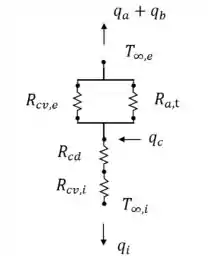
Nesse caso, temos aletas perdendo calor para o ambiente externo, além da área da base que também perde calor por convecção. Diante disso, é como se houvesse dois mecanismos em paralelo e o circuito pode ser representado da seguinte forma:
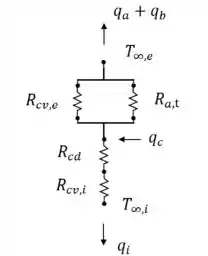
Em que:
Passo 2
Para as condições prescritas anteriormente, qual é a máxima taxa na qual o calor pode ser dissipado no chip quando os pinos estão no lugar? Isto é, qual é o valor de para ? O diâmetro e o comprimento do pino são respectivamente e .
Fazendo um balanço de energia na superfície do chip, a gente pode escrever que:
Em que:
- é a taxa de calor proveniente o chip.
- é a taxa de calor dissipada pelo conjunto de aletas.
- é a taxa de calor dissipada pela base do sistema para o ambiente externo.
- é a taxa de calor dissipada para o ambiente interno.
Passo 3
Bora agora calcular cada uma dessas taxas. Começando pela taxa de calor , podemos expressá-la em termos das resistências:
Calculando as resistências...
Para a resistência de convecção interna:
Dessa maneira, temos que:
Passo 4
Bora calcular agora a taxa de calor dissipada pela base da aleta ()!
Como é uma taxa de convecção, temos que:
A área de troca térmica será toda essa região em vermelho/rosa mais escuro, pois é a região que não foi ocupada por aletas:
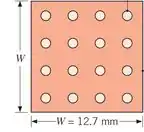
Então, a gente fica com:
Sendo assim:
Passo 5
Agora, finalmente, bora calcular a taxa de calor dissipada pelo conjunto de aletas ().
Em termos da resistência do sistema aletado:
Dessa equação, a gente só precisa determinar a eficiência da aleta () – via gráfico - e calcular a área total ()!
Ou a gente pode usar direto a equação da taxa que temos na tabela. Como essa situação se enquadra no caso (convecção na extremidade), a expressão da taxa é dada por:
O número multiplicando a expressão representa o número de aletas no sistema e:
Sendo assim:
Além disso:
Utilizando e os valores calculados na expressão, a gente fica com:
Passo 6
Pelo balanço de energia:
Resposta
- O circuito térmico é dado abaixo:
- A taxa de calor máxima do chip deve ser:
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Um aquecedor de ar consiste em um tubo de aço () com raios interno e externo e respectivamente e oito aletas longitudinais integrais, cada uma com espessura . As aletas se estendem até um tubo concêntrico de raio , o qual tem sua face externa isolada. Água à temperatura escoa através do tubo interno enquanto o ar à temperatura de escoa através da região anular formada pelo tubo concêntrico maior.
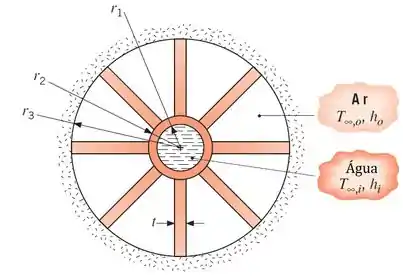
Esboce o circuito térmico equivalente do aquecedor e relacione cada resistência com os parâmetros apropriados do sistema.
Se e , qual é a taxa de calor por unidade de comprimento?
Passo 1
Esboce o circuito térmico equivalente do aquecedor e relacione cada resistência com os parâmetros apropriados do sistema.
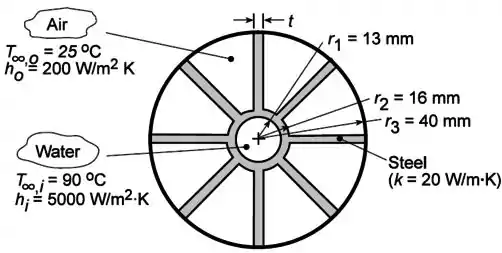
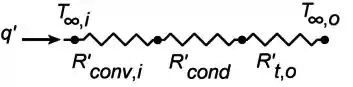
Em que:
Passo 2
Se e , qual é a taxa de calor por unidade de comprimento?
Pelo circuito térmico, a gente já sabe como escrever a taxa de calor que passa pelo sistema:
Bora calcular as resistências térmicas:
Passo 3
Para calcular a resistência térmica do sistema aletado, temos o seguinte:
Em que, representa a área de uma aleta sobre a unidade de comprimento e representa a área total do sistema aletado, inclusive a área da base que fica exposta.
Pra calcular essas áreas a gente pode considerar que o raio da superfície cilíndrica é muito maior que a espessura da aleta, então a gente pode admitir que a aleta é plana de seção retangular!
Bora lá! A gente tem que:
Sendo assim:
Agora só precisamos determinar a eficiência deste tipo de geometria de aleta (). Como as aletas são planas e retangulares, a gente tem o seguinte:
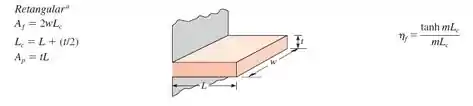
Em que:
Assim, temos que:
Dessa forma:
Passo 4
Agora a gente pode calcular a resistência térmica de contato do sistema aletado por:
E, finalmente, a taxa de calor por unidade de comprimento será:
Resposta
O circuito térmico é dado abaixo:
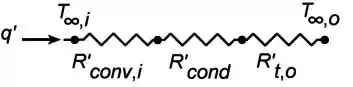
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Passagens alteradas são formadas frequentemente entre placas paralelas para elevar a transferência de calor por convecção em matrizes compostas de trocadores de calor. Uma aplicação importante encontra-se em resfriamento de equipamentos eletrônicos, em que um ou mais canais de ar resfriado são colocados entre componentes elétricos que dissipam calor. Considere um canal simples de aletas retangulares de comprimento e espessura , com condições de convecção correspondentes a e .
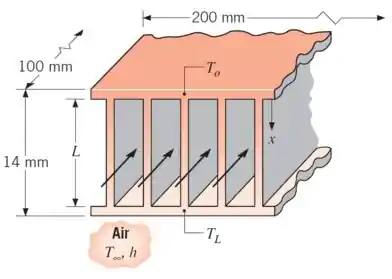
Obtenha expressões para as taxas de transferência de calor da aleta ( e ) em função das temperaturas da base (e ).
Em uma aplicação específica, um canal com de largura e de profundidade contém aletas, casa uma com comprimento . O canal é feito em alumínio () com de espessura ao longo de sua extensão. Se as limitações de temperaturas associadas com os componentes elétricos fixados no lado oposto da placa estabelecem a máxima temperatura permitida na placa e , quais são as potências dissipadas correspondentes de e ?
Passo 1
Obtenha expressões para as taxas de transferência de calor da aleta ( e ) em função das temperaturas da base (e ).
A solução geral para a distribuição de temperatura é dada por:
A gente pode propor as seguintes condições de contorno:
Substituindo na equação:
Dessa maneira:
E, substituindo essa expressão de na equação, a gente consegue achar ainda a constante :
Finalmente, temos que o perfil de temperatura é dado por:
Reorganizando:
Ou, em termos de funções trigonométricas hiperbólicas:
Passo 2
Para encontrar a taxa de calor da aleta, vamos usar a equação de Fourier:
Então, a gente precisa da derivada do perfil de temperatura. Bora calcular então:
A área pode ser calculada como:
Substituindo essas expressões na equação de Fourier:
Na posição , temos:
Na posição , temos:
Passo 3
Em uma aplicação específica, um canal com de largura e de profundidade contém aletas, casa uma com comprimento . O canal é feito em alumínio () com de espessura ao longo de sua extensão. Se as limitações de temperaturas associadas com os componentes elétricos fixados no lado oposto da placa estabelecem a máxima temperatura permitida na placa e , quais são as potências dissipadas correspondentes de e ?
Para calcular as taxas, a gente precisa determinar o valor de , então bora lá:
Substituindo os valores
Assim, o produto vale:
Dessa maneira, na posição , temos:
Dessa maneira, na posição , temos:
Resposta
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
(Adaptada) Propõe-se para o resfriamento do ar de um cilindro de câmara de combustão a colocação de um conjunto de aletas anulares () na parede do cilindro ().
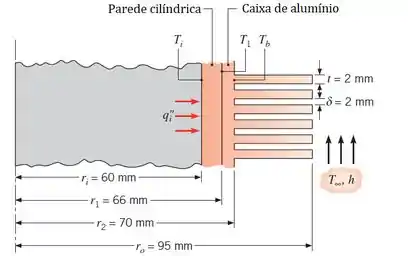
O ar está a e o coeficiente de convecção correspondente é . Mesmo o aquecimento da superfície interna sendo periódico, é razoável considerar condições de regime estacionário com um fluxo de calor médio de .
Considerando desprezível a residência de contato entre a parede e a aleta, determine a temperatura interna da parede ().
Passo 1
Podemos representar a situação com o seguinte esquema:
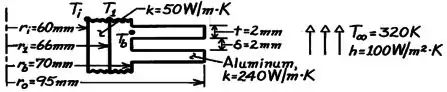
O circuito que representa o sistema é ilustrado abaixo:
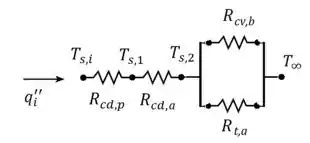
Em que:
Passo 2
A gente pode, então, escrever a taxa de calor em termos das resistências:
Bora calcular as resistências! Começando pela condução na parede:
Para a condução na base da aleta:
Para a convecção na base da aleta:
Como a espessura da aleta () e o espaçamento entre elas () são iguais, a gente pode considerar que a área da base () é metade de toda a área cilíndrica (se não tivesse aletas) e metade é ocupada por aletas. Sendo assim:
Passo 3
Agora, bora calcular a resistência térmica do sistema aletado:
Temos que determinar a eficiência da aleta (). Para isso, vamos utilizar o gráfico desse tipo de geometria:
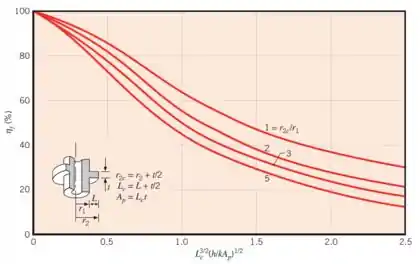
Precisamos, então, saber qual das quatro curvas representa nosso problema e qual o valor de do gráfico. Então, bora lá:
Passo 4
Agora, vamos à resistência que mais interessa:
- Resistência térmica de uma aleta anular simples:
Da expressão aqui em cima, a gente só sabe o coeficiente , mas precisamos determinar a área () e eficiência da aleta ().
A área da aleta é essa área aqui em vermelho:
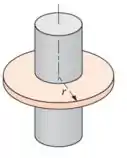
Então, a gente pode escrever que:
Mas a gente pode usar aquela estratégia do raio corrigido (), que é quando a gente assume que a contribuição da área lateral é adicionada à área do disco. Sendo assim:
Em que:
Substituindo os valores do enunciado:
Passo 5
Agora só falta a eficiência ()! Pra calcular a eficiência desse formato de aleta (anular), a gente tem que utilizar o gráfico que já vimos:
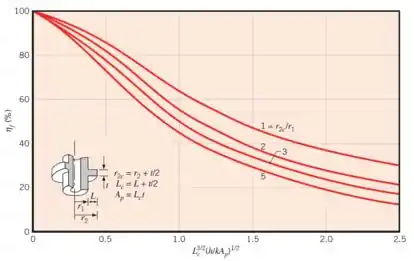
Para determinar a eficiência, a gente precisa então saber qual das quatro curvas representa a nossa aleta e calcular com o valor desse eixo aí loucão. Então, bora lá!
Bora calcular o valor de x do gráfico:
Em que e são calculados pelas expressões mostradas no gráfico:
Além disso:
Ufa! Agora a gente pode finalmente calcular o valor de x:
Pra saber qual das curvas serve pra gente, precisamos calcular a razão entre os raios:
Não tem nenhuma curva com esse valor, mas a gente pode colocar mais ou menos entre as curvas de razão igual a e , um pouco mais próximo da curva de .
Agora a gente já pode marcar no gráfico a posição da abscissa e ver a eficiência correspondente:
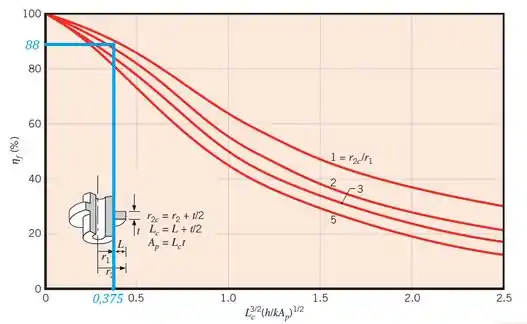
Concluimos, assim, que:
Passo 6
Com a área e eficiência calculadas, a gente pode finalmente determinar a resistência térmica da aleta:
Logo:
Passo 7
Como a gente viu, a taxa de calor por ser escrita como:
E a taxa pode ser escrita em termos do fluxo:
Dividindo a expressão pelo comprimento:
Isolando a temperatura da superfície mais interna (), a gente fica com:
Resposta
Exercício Resolvido #6
Questão 4, UFF, P1-2015.1
São colocadas 100 aletas em formato de disco igualmente espaçadas de em uma tubulação de de comprimento total. As aletas e a tubulação são de aço inoxidável 304.
Os discos possuem uma espessura de cada. A tubulação tem um diâmetro externo de e as aletas possuem de tamanho (diâmetro do disco da aleta é de ).
Admitindo que a temperatura da base (tubulação) seja de , qual é a quantidade de calor perdida para o ambiente considerando que o fluido ambiente está a e existe um coeficiente de película de .
Foi uma boa ideia colocar esse conjunto de aletas?
Assuma as propriedades termofísicas do aço inoxidável 304 constantes e iguais ao valor destas a .
Não é necessário desenvolver as soluções analíticas para esse problema. Utilize as informações previamente desenvolvidas e conhecidas.
Passo 1
Admitindo que a temperatura da base (tubulação) seja de , qual é a quantidade de calor perdida para o ambiente considerando que o fluido ambiente está a e existe um coeficiente de película de .
A taxa de transferência de calor total no sistema será dada por:
Onde é a eficiência global da superfície, dada por:
Onde é a área de troca térmica de uma aleta, é a área total do sistema e é a eficiência de uma aleta.
Passo 2
A área superficial de uma aleta anular é dada por:
Onde:
Assim:
A área total do sistema “aleta+base” é dada por:
Passo 3
Precisamos agora calcular o rendimento de uma aleta única (). Para isso, vamos usar a seguinte equação:
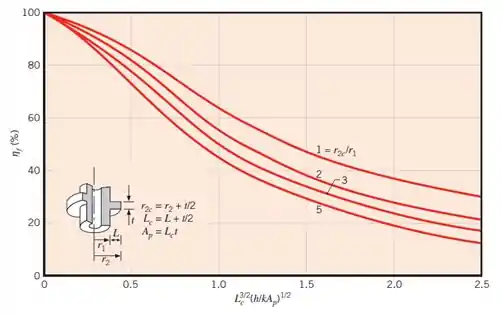
Onde:
Jogando esses valores na expressão da abscissa, onde :
Pra saber qual das curvas serve pra gente, precisamos calcular a razão entre os raios:
Como o valor de é muito grande, não temos como buscar exatamente o quanto vale a eficiência, então vamos estimar uma eficiência em torno de . Assim:
Passo 4
A eficiência global do sistema será:
Assim, a taxa de transferência de calor será:
![]()
Passo 5
Foi uma boa ideia colocar esse conjunto de aletas?
Caso não houvesse aletas, a taxa de transferência de calor, considerando o mesmo coeficiente convectivo seria:
![]()
Assim, como a ideia de um sistema aletado é aumentar a taxa de transferência de calor, foi uma boa ideia colocar esse conjunto de aletas, pois ele irá aumentar a taxa de transferência de calor.
Resposta
Não foi uma boa ideia colocar esse conjunto de aletas, pois ele irá diminuir a taxa de transferência de calor.