Equação da Aleta
Produzido por Giovanna RonzéTeoria
Bora entender de uma vez por todas como ocorre a condução em superfícies aletadas?!
O que é uma aleta?
A aleta é uma extensão da superfície usada para aumentar a área de troca térmica e consequentemente sua taxa de transferência de calor .
Mas calma, vou te explicar melhor! Se liga no esqueminha abaixo:
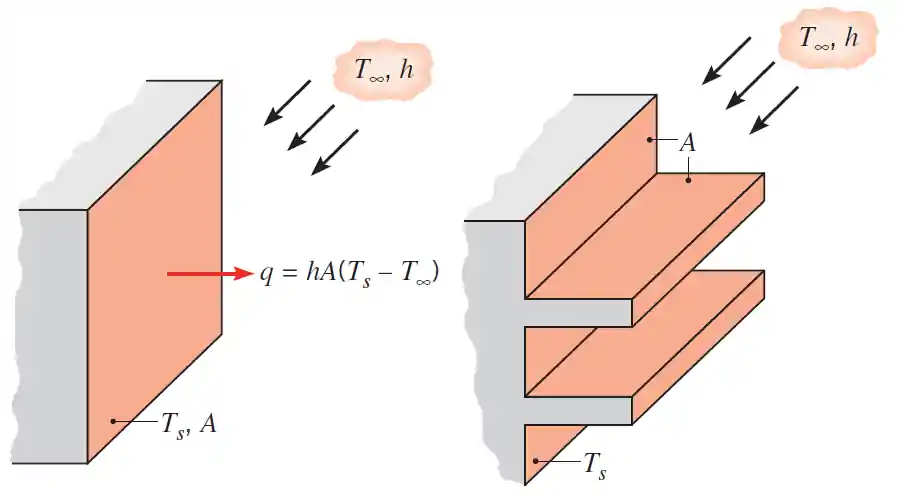
Na figura acima temos o aumento da área de troca térmica com um conjunto de aletas. Mas pra as coisas ficarem mais claras, dar um passinho pra trás!
Quando a gente estuda convecção, vemos que uma superfície a certa temperatura
Mas imagina que você não tá satisfeito com a quantidade de calor que tá sendo trocada entre a superfície e o fluido. Você quer aumentar a taxa de energia! O que você faria?
Se a taxa de calor trocado por convecção
Beleza! Mas as vezes é difícil alterar o
Tipos de Aletas
Existem vários tipos de aleta, a imagem abaixo nos mostra os principais tipos de aletas:
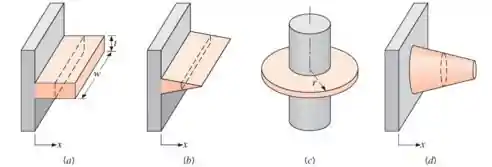
As aletas podem ser planas de seção transversal uniforme (a) ou plana de seção transversal não uniforme (b), ou ainda ser uma aleta anular (c) e até em forma de pino (d).
A equação geral da aleta é dada por:
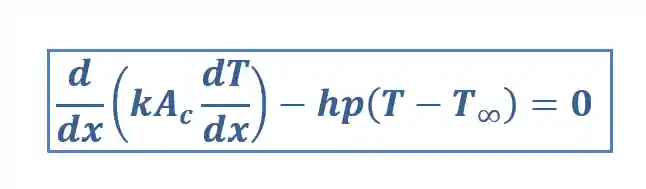
Onde
Então bora entender como ela funciona e quais são as suas condições de contorno?! 😉
Aletas com Seção Transversal Uniforme
Primeiro a gente vai determinar a distribuição de temperatura em aletas.
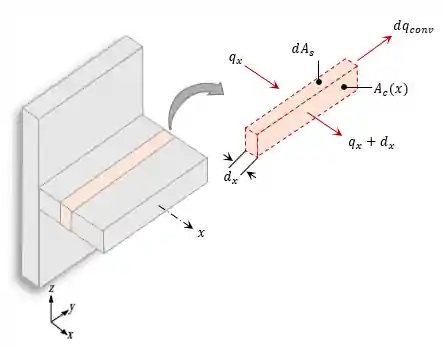
Pra isso, vamos fazer o seguinte balanço de energia num elemento infinitesimal da aleta:

No caso em particular que estamos considerando, onde a seção transversal
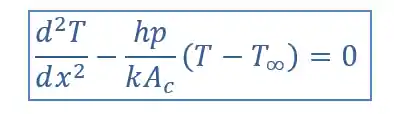
O perfil de temperatura geralmente é escrito em termos de
Onde:
A solução da equação diferencial em
Beleza! Pra encontrar as constantes
A condição de contorno na extremidade pode dividida em 4 casos:
Caso A: Convecção na Extremidade
Nesse caso consideramos que existe convecção na extremidade da aleta, e não só no seu comprimento.
Caso B: Extremidade Adiabática
Aqui, diferente do caso A, a extremidade da aleta não troca calor!
Caso C: Extremidade Com Temperatura Constante
Nesse caso a temperatura na extremidade da aleta permanece com a temperatura igual a temperatura inicial.
Caso D: Aleta Infinita
Por fim temos o caso da aleta infinita, que é usado quando as aletas tem um comprimento tão grande, que o calor nunca chega na sua extremidade!
As distribuições de temperatura e as taxas de calor para cada condição de contorno, podem ser observadas na figura abaixo:

Aletas: Vídeo Aula
Agora se liga nessa vídeo aula com um resumo super completo sobre aletas!
Agora vamos praticar com exercícios?
Aletas com Seção Transversal Uniforme
Aletas: Vídeo Aula
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Um longo bastão circular de alumínio tem uma de suas extremidades fixada a uma parede aquecida e transfere calor por convecção para um fluido frio.
Se o diâmetro do bastão fosse triplicado, qual seria a mudança na taxa de remoção de calor através do bastão?
Se um bastão de cobre com o mesmo diâmetro fosse usado em lugar do bastão de alumínio, qual seria a mudança na taxa de remoção de calor através do bastão?
Dado: e .
Passo 1
Se o diâmetro do bastão fosse triplicado, qual seria a mudança na taxa de remoção de calor através do bastão?
Quando o problema nos diz que o bastão é longo, isso quer dizer que podemos considerar o Caso D da nossa teoria, ou seja, de uma aleta infinita.
Se olharmos na tabela, veremos que, pra esse caso, a taxa de transferência de calor é dada por:
Como estamos trabalhando com uma aleta cilíndrica, teremos:
Logo:
Como estamos preocupados apenas com o que acontece quando mudamos o diâmetro (ou seja, as outras variáveis permanecem constantes), podemos ver pela equação acima que a taxa de transferência de calor é proporcional a :
Passo 2
Agora que encontramos a relação entre a taxa de transferência de calor, podemos analisar o que acontece com a mesma se triplicarmos o diâmetro:
Passo 3
Se um bastão de cobre com o mesmo diâmetro fosse usado em lugar do bastão de alumínio, qual seria a mudança na taxa de remoção de calor através do bastão?
Olhando novamente para a equação da taxa de transferência de calor:
Vemos que, nesse caso, a mesma será proporcional , logo, ao mudarmos o material:
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Uma barra circular longa de de diâmetro tem uma extremidade mantida a . A superfície da barra está exposta ao ar ambiente a com um coeficiente de transferência de calor por convecção de .
- Determinar a distribuição de temperatura ao longo da barra construída de cobre puro ().
- Qual a perda correspondente de calor a partir da barra?
- Estimar o comprimento da barra para que a hipótese de comprimento infinito forneça uma estimativa precisa para a perda de calor.
Passo 1
a) Pra gente determinar a distribuição de temperatura na aleta, a gente pode usar as equações que estão na tabela! A situação ilustrada pelo enunciado refere-se ao caso , pois o enunciado diz que a barra é longa.
Então, se a gente admitir que a barra tem comprimento infinito, sua superfície mais extrema terá a mesma temperatura que o fluido () e a equação do perfil de temperatura nessa situação será:
Ou seja:
A distribuição de temperatura é exatamente a expressão que descreve a temperatura ao longo de , então isolando o termo , a gente fica com:
Em que:
O termo é referente ao perímetro superfície mais extrema, ou seja, o perímetro da circunferência de diâmetro e o termo se refere à área dessa superfície!
Dessa maneira:
Logo:
Dessa maneira, a distribuição de temperatura na barra é dada por:
Passo 2
b) A gente pode obter a taxa de calor diretamente pela tabela também:
Substituindo os valores do enunciado:
Passo 3
c) Admitindo que a barra é muito longa, a temperatura da extremidade terá a mesma temperatura que o fluido, então ali não haverá perda de calor (não existe gradiente de temperatura).
E, se você der uma olhada na nossa tabela de fórmulas, você vai ver que existe uma expressão para a condição de superfície adiabática.
Nessa condição, a taxa de calor é dada por:
“Mas, se a superfície é adiabática, como que tem troca de calor?”. A extremidade é adiabática, mas o restante da superfície troca energia com o ambiente!
Como a gente quer que a taxa de calor no caso adiabático seja igual à taxa no caso de aleta de comprimento infinito, a gente poderia simplesmente igualar as expressões de cada um:
Essa equação só é satisfeita para tendendo ao infinito! Isso não é possível fisicamente! Então, o que a gente pode fazer é assumir que se a taxa chegar a do valor, isso já será suficiente! Bora ver no que dá então:
Essa equação é satisfeita para:
Como já calculamos o na letra a), a gente tem que:
Pronto! Esse é o comprimento da barra que a gente já pode considera-la infinita! Então, o comprimento pode ser maior ou igual a .
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
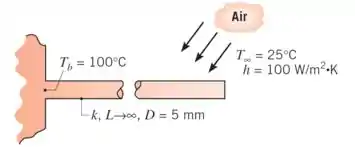
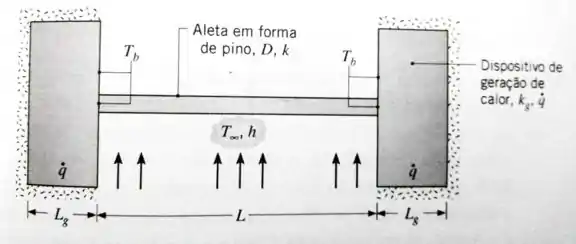
Aletas em forma de pino são amplamente utilizadas em sistemas eletrônicos para promover resfriamento, bem como suporte de componentes. Considere uma aleta em forma de pino de diâmetro uniforme , comprimento e condutividade térmica conectando dois componentes de comprimento e área de superfície . Os componentes são caracterizados por uma geração volumétrica de energia térmica e condutividade térmica . Considere que as superfícies expostas dos componentes estão a uma temperatura uniforme correspondente àquela da base da aleta pino () e que o calor é transferido por convecção da superfície exposta para um fluido em contato. A parte posterior e as laterais dos componentes estão perfeitamente isoladas.
Deduza uma expressão para a temperatura da base em função dos parâmetros do componente (, , e ), dos parâmetros de convecção ( e ) e dos parâmetros da aleta (, e ).
Passo 1
Observamos que haverá troca de calor, por condução, no interior da aleta e, por convecção, nas superfícies dos componentes e da aleta.
Devido à simetria do problema, a gente pode resolver só um dos lados e afirmar que acontece o mesmo do lado oposto. Com isso, dizemos que as duas metades não trocam calor entre si e vamos usar as equações do caso B de aleta adiabática na extremidade:
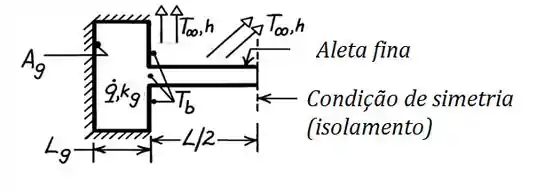
Essa estratégia é a mesma que fazemos com uma parede plana de condições de contorno simétricas.
Pelo balanço de energia na superfície de controle:
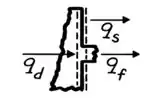
Então, a gente tem uma taxa de energia que entra (proveniente da geração de calor) e parte dessa energia sai pela aleta () e parte sai pela superfície lisa ():
Tudo que está entrando de energia nessa superfície () vem da geração volumétrica na parede. Então, a gente pode fazer um balanço de energia na parede pra expressar essa taxa de entrada ():
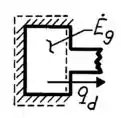
Em termos dos dados geométricos que temos, o volume pode ser reescrito:
Substituindo no balanço de superfície, a gente fica com:
Agora a gente precisa achar uma expressão para a taxa de calor que sai pela superfície plana () e a taxa de calor que sai pela aleta ()!
Passo 2
Bora determinar primeiro o mais fácil: a taxa de calor pela superfície lisa ()! Isso é simplesmente uma convecção sobre uma superfície, então a gente calcula pela lei de resfriamento de Newton:
Nesse caso a temperatura da superfície é a mesma da base () e a área de troca térmica da parede lisa será:
Substituindo os valores da aleta:
Logo:
Passo 3
Agora, a gente precisa calcular a taxa de calor da aleta!
A aleta em questão se enquadra no caso , então a taxa de calor perdida por ela pode ser escrita como:
Em que:
Bora calcular cada um deles então!
A área já foi calculada antes e o perímetro é dado por:
Logo:
E ainda:
Substituindo na expressão da taxa de calor da aleta:
Passo 4
Substituindo as expressões do calor trocado pela superfície plana () e pela aleta () no balanço de energia na superfície:
Isolando a temperatura da base ():
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Um bastão de latão com de comprimento e de diâmetro se estende horizontalmente a partir de uma solda a . O bastão encontra-se em um ambiente com e .
Quais são as temperaturas no bastão a , e da solda?
Passo 1
De acordo com o enunciado, a extremidade está sob convecção, o que corresponde ao Caso A da nossa tabela, logo:
Onde:
Substituindo os valores:
Agora basta testar com os valores que o problema pediu.
Passo 2
Resposta
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Dois longos bastões de cobre , com diâmetro , serão soldados pelas extremidades com uma solda com ponto de fusão de . Os bastões encontram-se em um ambiente a com um coeficiente de transferência de calor igual a .
Qual é a menor alimentação de potência necessária para efetuar a soldagem?
Passo 1
A ideia aqui é a seguinte:
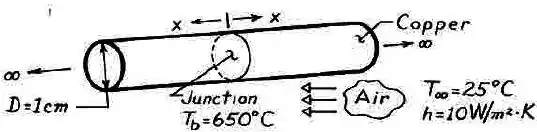
Como estamos tratando os dois bastões de cobre como longos, ambos correspondem ao Caso D da nossa tabela.
Assim, a taxa de transferência de calor necessária para manter a extremidade de cada bastão à temperatura de vai ser dada por:
Assim, como precisamos manter as das duas extremidades das duas à mesma temperatura, a quantidade mínima de potência necessária será:
Passo 2
Dados:
Substituindo os valores:
Resposta
Exercício Resolvido #6
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Bastões circulares de cobre , com diâmetro e comprimento , são usados para aumentar a transferência de calor em uma superfície mantida a .
Uma extremidade do bastão é presa a essa superfície (em ), enquanto a outra extremidade () é conectada a uma segunda superfície, mantida a . Ar, escoando entre as superfícies (e sobre os bastões), também se encontra a uma temperatura , mantendo um coeficiente convectivo .
Qual é a taxa de transferência de calor por convecção entre um único bastão de cobre e o ar?
Qual é a taxa total de transferência de calor dissipada de uma seção da superfície a com dimensões de por , se for instalado um feixe de bastões com distância entre os centros de ?
Passo 1
Qual é a taxa de transferência de calor por convecção entre um único bastão de cobre e o ar?
Vamos começar fazendo um balanço de energia nesse cara, a ideia é essa:
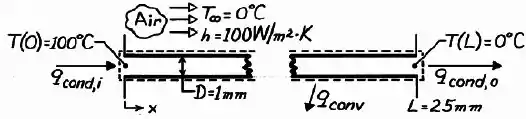
Opa! O problema está me falando que a temperatura na extremidade da barra é constante! Isso corresponde ao Caso C da tabela na Teoria!
Logo:
Show de bola, vamos trabalhar nessa equação!
Passo 2
Nessa equação, como :
Daí, podemos simplificar a equação:
Onde:
Logo:
Agora é arrumar a bagunça:
Multiplicando em cima e embaixo por :
Finalmente:
Passo 3
Agora que encontramos como a temperatura varia ao longo de , podemos calcular a taxa de transferência de calor por condução em função de :
No início e no final do bastão, a taxa de transferência de calor será:
Passo 4
Voltando para a expressão a taxa de transferência de calor por condução:
Sendo :
Pra não embolar, vamos calcular cada coisa separadamente, ok?
Logo:
Passo 5
Qual é a taxa total de transferência de calor dissipada de uma seção da superfície a com dimensões de por , se for instalado um feixe de bastões com distância entre os centros de ?
Estando os bastões distantes de entre seus centros, a quantidade de bastões que cabe em será:
Assim, no total, teremos:
Dessa forma, a taxa total de transferência de calor será a soma da taxa de transferência por condução de cada bastão com a taxa de transferência por convecção da área não ocupada pelos bastões, logo:
Onde:
Logo:
Resposta
Exercício Resolvido #7
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Sejam dois bastões longos e delgados de mesmo diâmetro, porém feitos de materiais diferentes. Uma extremidade de cada bastão está fixada a uma superfície (base) mantida a , enquanto as suas superfícies estão expostas ao ar ambiente a .
Ao mover ao longo do comprimento de cada bastão um termopar, foram observadas temperaturas iguais nas posições e , onde é medido a partir da base.
Se a condutividade térmica do bastão é conhecida e igual a , determine o valor de para o bastão .
Passo 1
Vamos nessa! O problema nos diz que ambos os bastões são longos, certo?!
Então, para ambos vamos considerar o Caso D da nossa tabela na Teoria, ou seja, o caso de aletas infinitas.
Nesse caso, a distribuição de temperatura é dada por:
Passo 2
De acordo com o problema, os dois bastões apresentam a mesma temperatura em e . Dessa forma, podemos dizer que:
Igualando as duas expressões, temos que:
Substituindo a expressão de para cara bastão:
Elevando os dois lados ao quadrado:
Onde:
Logo:
Resposta
Exercício Resolvido #8
Questão 3, PUCRIO, P1-2003
Uma aleta cilíndrica deve ser utilizada para aumentar em a troca de calor entre uma parede e o ambiente. A parede tem a temperatura mantida a , e está exposta ao ar ambiente a .
O coeficiente de troca de calor por convecção entre a aleta e o ambiente vale . A aleta deve ser construída com um material de condutividade térmica igual a .
Considerando condução unidimensional e que o comprimento da aleta tende ao infinito , determine o raio da aleta e a expressão para a variação de temperatura ao longo da aleta.
Passo 1
Se considerarmos somente a região onde a aleta está presente, a taxa de transferência de calor entre a parede (considerando uma área referente à base da aleta) e o ambiente será:
Como a aleta tem a função de aumentar em a troca de calor entre a parede e o ambiente, após a colocação da mesma, temos que:
Passo 2
De acordo com o problema, podemos considerar o Caso D da nossa teoria, ou seja, de uma aleta infinita.
Se olharmos na tabela, veremos que, pra esse caso, a taxa de transferência de calor é dada por:
Como estamos trabalhando com uma aleta cilíndrica, teremos:
Logo:
Substituindo os valores:
Passo 3
Igualando as expressões para a taxa de transferência de calor na aleta:
Passo 4
Ainda de acordo com a tabela, a distribuição de temperatura é dada por:
Onde:
Assim: