Transferência De Calor - Mecanismos
Produzido por Giovanna RonzéTeoria
Fala aí! Hoje vamos trocar uma ideia de uma maneira mais introdutória sobre transferência de calor e seus principais mecanismos: condução, convecção e radiação.
Já dando um spoiler, a transferência de calor ocorre sempre que existe uma diferença de calor entre dois meios. 🤔
Animou? Então bora lá ver cada um dos mecanismos de tranferência de calor com mais detalhe. Vem comigo!
Ah, já mencionei ali em cima mas vou ressaltar: essa página aqui vai ter uma pegada mais introdutória para mecanismos de transferência de calor, beleza? Mas fica tranquilo, se achar tudo isso muito básico e quiser se aprofundar um pouquinho mais em alguns dos tópicos que veremos aqui separadamente, vou deixar uns links que podem ser bem interessantes pra você, junto com um videozinho maravilhoso caso você prefira aprender esse conteúdo assim 👇🥰
⭐ Veja também ⭐
- Introdução à condução.
- Introdução à convecção.
- Introdução à radiação.
- Principais assuntos de FenTrans, MecFlu, TransCal e TransMassa.
Condução Térmica
Quando essa transferência ocorre a nível molecular, diz-se que ocorre a condução térmica.
A condução acontece em meios sólidos, líquidos e gasosos, por meio de colisões entre átomos e moléculas adjacentes. Assim, as partículas mais energéticas transferem energia para as menos energéticas, da região de maior temperatura para a de menor.
Já que a transferência de calor aqui é um processo que parece ser função de outros fatores, será que a gente consegue encontrar um meio de descrevê-la matematicamente?
Lei de Fourier
A Lei de Fourier é a lei fundamental que descreve a condução térmica.
Se liga, vamos imaginar que a figura abaixo representa uma parede, de espessura L, a qual separa um ambiente externo de um interno.
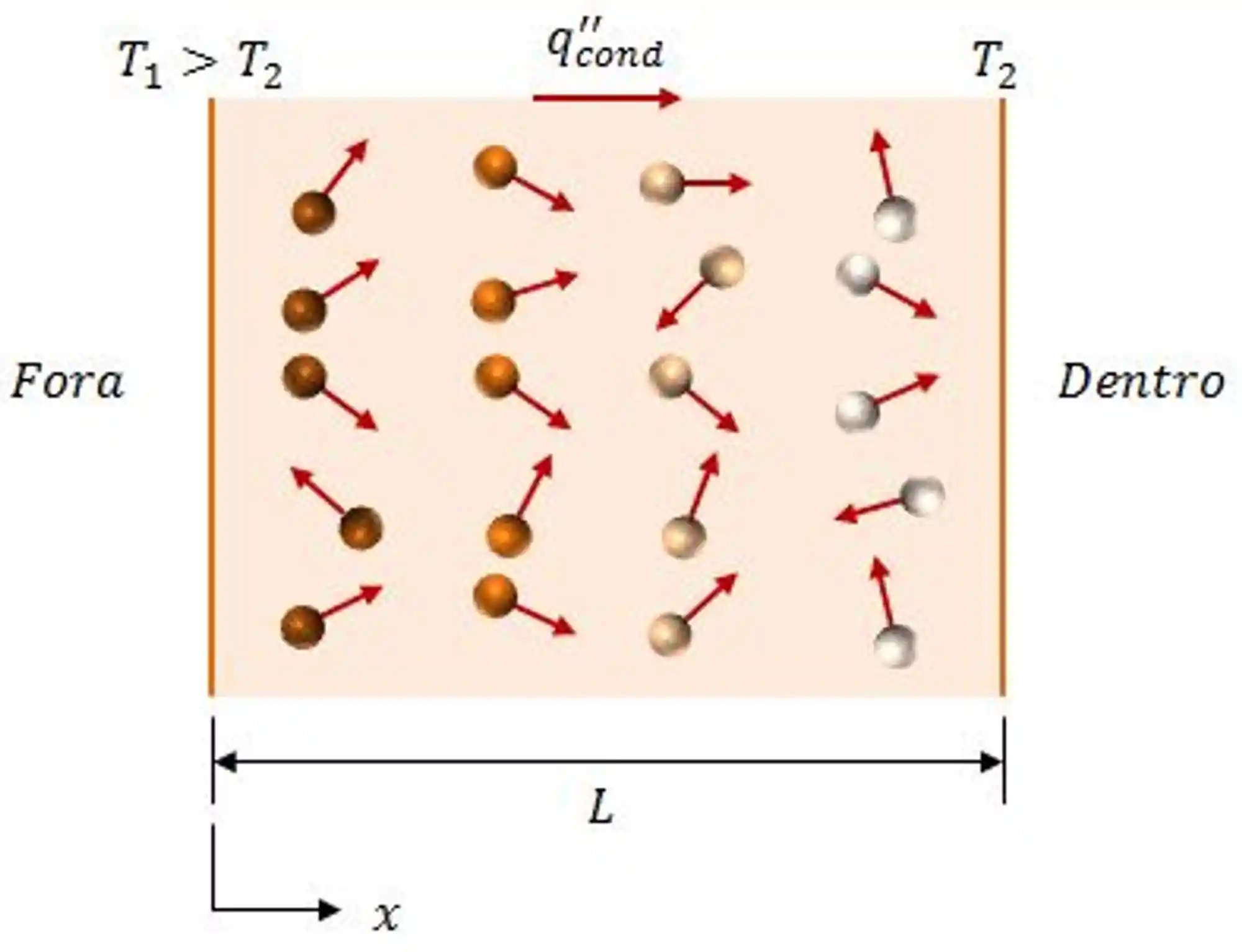
Vou te explicar o que é cada coisa aí!
A parte do lado de fora está a uma temperatura,
A gente chama essa transmissão de energia de calor. E o fluxo de calor por condução,
Esse k que apareceu ali é a condutividade térmica do meio em que o calor se propaga.
Repara que essa temperatura varia somente com a coordenada x. Maaas, se me permite um spoiler, em outros momentos veremos o que acontece se tivermos diferenças de temperaturas em outras direções também 😉
Quando aquele fluxo é constante, a gente pode integrar aquela equação pra chegar na seguinte fórmula para a condução:
A diferença entre as temperaturas de cada região é dada pelo
Convecção Térmica
A convecção descreve a transferência de calor em um fluido em movimento. Por se tratar de fluidos, esse processo aqui só vai acontecer em líquidos e gases, mas sempre em conjunto com a condução térmica que vimos anteriormente!
A convecção pode ser natural, quando o fluido ao redor da superfície está em repouso (você deixa sua sopa quente esfriar ao longo do tempo), ou forçada, quando o fluido escoa sobre a superfície (você assopra a sopa para esfriá-la).
Lei de Resfriamento de Newton
A lei de resfriamento de Newton nos dá a fórmula que descreve o fluxo de calor por convecção de uma superfície com temperatura
Aquele h ali é o coeficiente de convecção. Ele depende de vários parâmetros, tais como o tipo do fluido, sua temperatura, velocidade de escoamento, entre outros.
Radiação Térmica
Todos os mecanismos que vimos até agora requerem um meio, seja sólido, líquido ou gasoso, para o calor se propagar. Para a radiação, não precisa de meio nenhum para que ocorra propagação de calor!
Mas isso não quer dizer que não vai ocorrer transferência de calor por radiação nesses meios, viu? A radiação térmica pode ocorrer através de sólidos, líquidos, gases e também no vácuo!
Lei de Stefan-Boltzmann
A Lei de Stefan-Boltzmann fornece a fórmula a que vai descrever o fluxo de calor por radiação:
Aí aparecem duas constantes. A emissividade
Tranquilinho? Bora fazer alguns exercícios e depois partir para os conteúdos mais avançados!
Convecção Térmica
Radiação Térmica
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Uma janela de vidro de de largura e de altura apresenta de espessura e condutividade térmica de . Se as temperaturas interna e externa do vidro em um dia de inverno são e respectivamente, responda:
Qual a taxa de perda de calor através do vidro?
Para reduzir as perdas de calor através das janelas, costuma-se utilizar construções com painel duplo, em que as duas placas de vidro são separadas por ar. Se o espaçamento entre elas for de e as superfícies em contato com o ar tiver temperaturas de e , qual a taxa de perda de calor de uma janela ? A condutividade térmica do ar é .
Passo 1
a) O enunciado fala de uma janela de vidro com dimensões com temperaturas interna e externa conhecidas, como mostrado aqui no esquema:
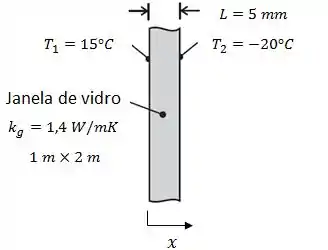
A primeira coisa que temos que fazer é encontrar a taxa de calor que passa através desse vidro. Sabemos que essa taxa é dada por:
Teremos um fluxo de calor no sentido da espessura do vidro, que definimos como eixo x. Como o calor flui do corpo mais quente para o corpo mais frio, a taxa de perca de calor acontece da esquerda para a direita, no sentido positivo do eixo x.
Passo 2
Qual a taxa de perda de calor através do vidro?
Como o calor está sendo transferido por condução através da janela, vamos usar a Lei de Fourier para determinar o fluxo de calor:
Nesse caso, como estamos trabalhando com um problema de placa plana, podemos escrever a Lei de Fourier da seguinte forma:
Juntando essa expressão com a que escrevemos no Passo 1, a taxa de transferência de calor por condução será dada por:
Como , o calor será transferido da esquerda para a direita, no sentido positivo do eixo , logo:
Onde:
Obs.: Um detalhe importante aqui! Como estamos calculando uma variação de temperatura, podemos, neste caso, utilizar a temperatura tanto em graus Celsius ou Kelvin já que, nas duas escalas o cálculo da variação de temperatura nos dará o mesmo valor.
Substituindo os valores:
Passo 3
Para reduzir as perdas de calor através das janelas, costuma-se utilizar construções com painel duplo, em que as duas placas de vidro são separadas por ar. Se o espaçamento entre elas for de e as superfícies em contato com o ar tiver temperaturas de e , qual a taxa de perda de calor de uma janela ? A condutividade térmica do ar é .
Agora que colocamos duas janelas de vidro uma do lado da outra, deixando um espaço entre elas ocupado por ar, a ideia é a seguinte:
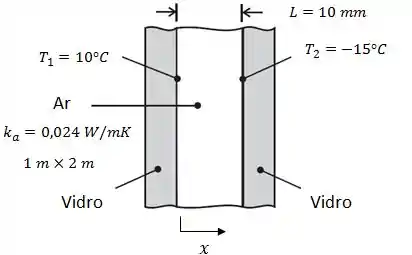
Se o objetivo é reduzir a perca de calor através da janela, então esperamos encontrar uma taxa de perda de calor menor do que encontramos na letra a. Considerando que a engenhoca funcione, teremos um cômodo mais quentinho do que no primeiro caso, certo? Logo a temperatura interna da janela deverá ser maior que 15ºC!
Então como a gente pode calcular a taxa de perda de calor se não sabemos a temperatura interna da janela? Calma, vem comigo!
Temos um regime permanente, isso quer dizer que a janela não pode nem gerar, nem acumular energia (que aqui aparece na forma de calor), logo a taxa de perda de calor através janela é igual a taxa de perda de calor através do espaço entre as placas de vidro.
E essa a gente consegue calcular!!!
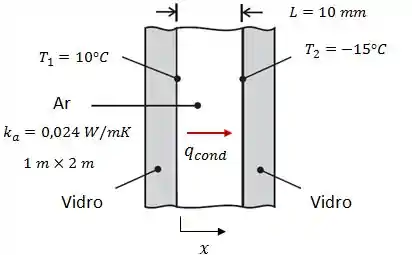
A taxa de calor transferida através do ar será:
Onde:
Substituindo os valores:
Lembrando que na letra a achamos, , que muuuuuito maior do que os 120W que terminamos de achar. Então vimos que essa engenhoca realmente funciona!!!
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Uma base com de espessura de uma panela com de diâmetro pode ser feita de alumínio () ou cobre (). Quando utilizada para ferver água, a superfície em contato com a água fervendo no fundo encontra-se nominalmente a . Se o calor é transferido a partir do fogão para a panela a uma taxa de , qual a temperatura da superfície em contato com o fogo para cada um dos materiais?
Passo 1
A ideia aqui é a seguinte, galerinha: o fogo está transferindo calor para a base da panela a uma taxa de , esse calor é então transferido por condução através da base da panela e, por último, esse mesmo calor é transferido para a água.
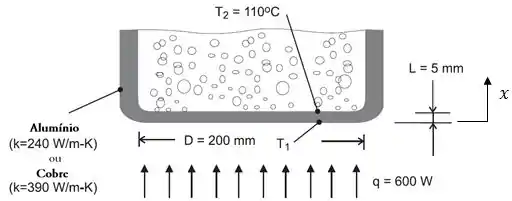
O problema nos deu as condutividades térmicas pra cada material, nos deu o diâmetro da base da panela, e nos disse que a temperatura na superfície que está em contato com a água vale .
Show de bola! Temos tudo o que precisamos pra calcular a temperatura da superfície em contato com o fogo para cada material.
Passo 2
Com a gente já discutiu, o mecanismo aqui nessa situação que é responsável pela transferência de energia é a condução! Então, utilizando a equação de Fourier, temos:
Como estamos tratando de um problema de placa plana, podemos escrever a Le ide Fourier da seguinte forma:
O fluxo de calor está relacionado à taxa de transferência de calor da seguinte forma:
Para que o calor seja transferido de baixo pra cima (no sentido positivo de ), é necessário que a temperatura na superfície em contato com o fogo seja maior que a temperatura da superfície em contato com a água .
Dessa forma, podemos escrever a Lei de Fourier da seguinte maneira:
Reorganizando essa equação podemos escrever que a temperatura da superfície em contato com o fogo será dada por:
Estamos com a faca e o queijo na mão! Agora é partir pro abraço!
Passo 3
Alumínio:
Onde:
Substituindo os valores:
Passo 4
Cobre:
Onde:
Substituindo os valores:
Note que a temperatura da superfície externa da panela é ligeiramente maior para o Alumínio, mas em ambos os casos a temperatura da superfície interna equivale a . Isso significa dizer que ambos materiais são muito bons condutores, pois quase não há diferença de temperatura entre a superfície interna e externa.
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Um transistor de comprimento e diâmetro é resfriado por uma corrente de ar de temperatura .
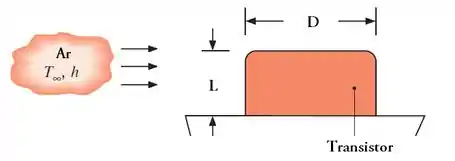
Em condições nas quais o ar mantém um coeficiente de convecção médio . Na superfície, qual a dissipação máxima de potência permitida se a temperatura da superfície não deve ultrapassar ?
Passo 1
O nosso objetivo é encontrar a taxa de calor que sai do transistor por convecção. Pelo enunciado a gente já tem informações com relação ao coeficiente de convecção (), a temperatura da superfície () e do fluido ().
Então, a gente consegue calcular o fluxo de calor pela lei de resfriamento de Newton:
Substituindo os valores:
Passo 2
Agora que já temos o fluxo, podemos calcular a taxa de dissipação da seguinte forma:
Como o problema nos deu o comprimento e o diâmetro do transistor, podemos concluir que esse cara é um cilindro. Assim, a área de troca térmica será soma da área lateral do cilindro com a área do topo com as dimensões informadas. Logo:
Onde:
Substituindo os valores:
Voltando para a taxa de dissipação:
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Um aquecedor elétrico de cartucho apresenta a mesma forma de um cilindro longo de comprimento e diâmetro . Em condições normais de operação, o aquecedor dissipa , quando submerso em uma corrente de água a em que o coeficiente de transferência de calor é de .
Desprezando a transferência de calor a partir dos terminais do aquecedor, determine sua temperatura de superfície .
Se a corrente de água for inadvertidamente interrompida enquanto o aquecedor continua operando, a superfície do aquecedor fica exposta ao ar que também se encontra a , mas para o qual . Qual a temperatura da superfície correspondente? Quais as consequências de tal ocorrência?
Passo 1
Desprezando a transferência de calor a partir dos terminais do aquecedor, determine sua temperatura de superfície .
Vamos nessa, meu time! Nessa questão, nosso objetivo será entender como o tipo de fluido (água e ar) em contato com um material afeta na dissipação de calor, verificando qual deles é mais eficiente em resfriar um determinado material que está aquecido.
Alguns fluidos têm uma capacidade maior de “roubar calor” das superfícies do que outros e o que quantifica essa habilidade é o coeficiente de convecção ().
O mecanismo responsável pela transferência de energia aqui nessa situação é a convecção! Então, utilizando a lei de resfriamento de Newton, temos:
O fluxo térmico está relacionado com a taxa de transferência de calor por convecção da seguinte forma:
O termo representa a área de troca térmica: é a área da superfície do material por onde ocorre a transferência de energia térmica. Como o aquecedor é cilíndrico, temos que a área total seria: área lateral + área da base + área do topo.
Entretanto, o enunciado pede pra gente desprezar a transferência de calor a partir dos terminais. Dessa forma, ficamos só com a área lateral:
Como o que nós queremos nos dois casos é determinar a temperatura da superfície, podemos reorganizar a equação acima da seguinte forma:
Passo 2
Pronto, agora a gente já pode avaliar a temperatura da superfície em cada um dos casos!
Para o caso com água escoando, teremos a dissipação de calor por convecção forçada:
Onde:
Substituindo os valores do enunciado:
Passo 3
Se a corrente de água for inadvertidamente interrompida enquanto o aquecedor continua operando, a superfície do aquecedor fica exposta ao ar que também se encontra a , mas para o qual . Qual a temperatura da superfície correspondente? Quais as consequências de tal ocorrência?
Se a corrente de água for interrompida, o aquecedor ficará somente com ar ao seu redor, provocando assim a convecção natural.
O aquecedor continua liberando a mesma taxa de , o que acontece é que o coeficiente de convecção do ar () é menor que o da água (), logo a energia “roubada” do aquecedor pelo fluido será menor no caso do ar do que no caso da água.
Novamente utilizando a expressão que encontramos para a temperatura na superfície:
Onde:
Substituindo os valores do enunciado:
Note que a temperatura, depois de interromper a corrente de água, fica absurdamente maior! Isso é exatamente o que a gente esperava! Quanto menor o coeficiente de transferência (), mais difícil é transferir energia do aquecedor para o fluido e, como a quantidade de energia (no tempo) que o aquecedor ele libera é constante (), mais energia fica “armazenada” nele no caso de um menor .
Uma das consequências de interromper a corrente de água seria a danificação dos componentes do aquecedor, pois a temperatura pode superar o ponto de fusão dos materiais envolvidos.
Resposta
.
. Uma das consequências de interromper a corrente de água seria a danificação dos componentes do aquecedor, pois a temperatura pode superar o ponto de fusão dos materiais envolvidos.
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
(Adaptada) “Em condições nas quais a mesma temperatura ambiente é mantida por um sistema de aquecimento ou resfriamento, é comum para uma pessoa sentir-se incomodada com um pouco de frio no inverno, mas confortável no verão”.
Dê uma explicação plausível para esta situação (com cálculos que apoiem sua colocação), considerando que a temperatura do ar ambiente seja mantida a durante todo o ano e as paredes da sala a no verão e no inverno. A superfície exposta de uma pessoa na sala pode ser considerada a uma temperatura de no decorrer do ano com uma emissividade de . O coeficiente associado à transferência de calor por convecção natural entre a pessoa e o ar ambiente é aproximadamente .
Passo 1
Essa questão aborda o terceiro mecanismo de transferência de energia que a gente viu na teoria: a radiação.
A situação que o enunciado descreve é que quando a gente programa o ar condicionado para que o ar ambiente esteja a uma temperatura de , a gente sente mais frio no inverno do que no verão dentro da sala.
A sensação de conforto térmico está associada a quantidade de energia que perdemos, então a gente precisa avaliar os fluxos de calor que saem do corpo.
Isso pode parecer meio louco, não é mesmo? Mas se você reparar, a temperatura da parede no verão é diferente daquela no inverno, apesar do ar ambiente nas duas situações estar a .
Dá uma olhada em como é a situação:
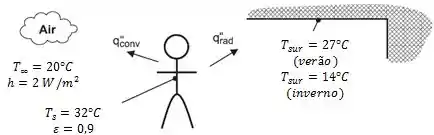
A temperatura do fluido () continua sendo , então o calor trocado por convecção será o mesmo. Já o calor emitido por radiação do corpo depende da temperatura do corpo () e das paredes que o envolvem ():
Então, se a temperatura das paredes é menor no inverno, a diferença de temperatura entre o corpo e as paredes será maior e, consequentemente, a energia perdida por radiação será maior.
Então bora fazer os cálculos pra comprovar isso!
Passo 2
O primeiro cálculo que faremos será para a situação no verão, temos que o fluxo de calor por radiação é dado por:
Onde:
Atenção! Lembre-se sempre de converter as temperaturas para Kelvin quando for calcular qualquer coisa relacionada à radiação, porque a diferença de temperatura em graus Celsius é igual em Kelvin, mas aqui temos a temperatura elevada à quarta potência!
Substituindo os valores:
Passo 3
Utilizando agora os dados para a situação de inverno, teremos:
Onde:
Substituindo os valores:
Veja que foi exatamente o que pensamos no início: o corpo perde mais energia por radiação no inverno do que no verão. Sendo assim, as pessoas tendem a sentir mais frio no inverno, mesmo a temperatura ambiente na sala estando igual. Bacana, não?
Resposta
As pessoas tendem a sentir mais frio no inverno do que no verão, mesmo a temperatura ambiente na sala estando igual, porque o fluxo de energia perdida pelos corpos por radiação é mais relevante no inverno. Isso acontece porque as paredes estão em uma temperatura menor e os corpos estão na mesma temperatura, assim diferença entre as temperaturas do corpo e das paredes é maior no inverno. Consequentemente, os fluxos por radiação no inverno () também são maiores que no verão ().