Soluções Tabeladas para Condução Transiente

Teoria

Introdução

Um dos principais objetivos quando estudamos a condução de calor é determinar a distribuição de temperaturas no interior de um corpo.

Para casos em que , podemos usar o Método dos Parâmetros Concentrados. Quando , temos a opção de usar o Método dos Efeitos Espaciais.

No entanto, quando estamos trabalhando com placas planas, podemos usar soluções tabeladas para resolver a equação de calor.

Vamos pensar na seguinte situação:

Uma placa de espessura , confinada a uma região , está inicialmente a uma temperatura uniforme . Em , a superfície é conservada isolada e a superfície em é mantida a uma temperatura constante .

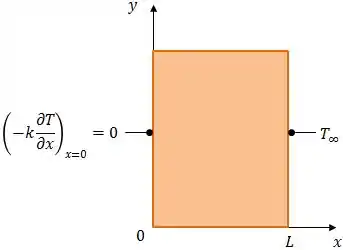
O nosso objetivo aqui é desenvolver a expressão da distribuição transiente de temperatura na placa.

Formulação Matemática do Problema

A equação de calor é dada por:

Para representar o nosso problema, vamos fazer as seguintes considerações:

Transferência de calor unidimensional;
Transferência de calor sem geração térmica ;
Propriedades térmicas constantes.

Dessa forma, a nossa equação de calor fica com essa cara:

Em que é a difusividade térmica do material.

Para que as condições de contorno sejam homogêneas, vamos definir uma nova temperatura , dada por:

Dessa forma, a equação de calor terá essa cara:

As condições de contorno serão de superfície isolada em , e superfície a temperatura constante em . Dessa forma:

E a condição inicial será dada por:

Soluções Tabeladas

A equação de calor que encontramos é resolvida através do método de separação de variáveis. O mesmo pressupõe que a função pode ser representada como o produto de duas funções que dependem de e , separadamente:

Aplicando esse método e resolvendo a equação de calor, podemos representar a temperatura como:

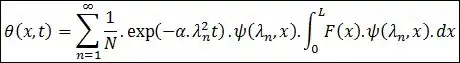
Tá, eu sei que assusta, então vamos entender quem é quem! A função corresponde à distribuição inicial de temperatura.

No nosso caso, como a placa está inicialmente a uma temperatura uniforme :

Além disso:

: Autofunções;
: Autovalores;
: Integral de normalização.

Esses três caras são justamente o que a nossa tabela irá fornecer. Assim, pra determinar esses caras, basta saber as condições de contorno, se liga:

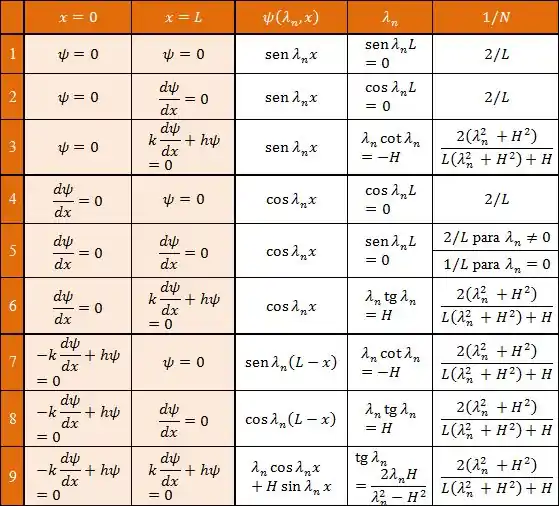
Onde .

Na tabela, temos as seguintes condições de contorno:

: Temperatura constante;
: Superfície isolada;
: Convecção na superfície.

Voltando ao nosso problema...

No nosso caso, temos uma condição de superfície isolada em e temperatura constante em .

Isso corresponde ao caso 4 da tabela. Dessa forma, a autofunção será:

Onde é o autovalor dado como solução da seguinte equação:

O cosseno será nulo para quando o ângulo assumir algum dos seguintes valores:

Logo, podemos dizer que:

E a integral de normalização será:

Dessa forma, substituindo tudo isso na expressão de , teremos:

Vamos resolver a integral separada pra não bagunçar demais:

Repare que, quando for par, o seno será igual a e, quando for ímpar, o seno será igual a . Assim, podemos reescrever o resultado acima como:

Substituindo na expressão da temperatura, teremos:

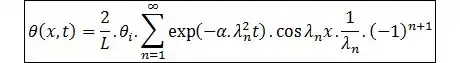
Onde:

Agora estamos prontos pra cair nos exercícios!

Soluções Tabeladas

Voltando ao nosso problema...

Exercícios Resolvidos

Exercício Resolvido #1

Questão 5, UFRJ, P1-2007.1

Considere condução de calor transiente e unidimensional em uma placa plana com propriedades constante e espessura .

A placa, que se encontra inicialmente na temperatura uniforme , troca calor através de sua superfície em por convecção com um meio na temperatura com coeficiente de transferência de calor .

A superfície em é mantida na temperatura constante . Sabendo-se que a geração de energia na placa é nula, forneça para este problema:

Formulação matemática.

Solução analítica.

Passo 1

Formulação matemática.

Para chegar à formulação matemática, vamos partir da equação de calor, dada por:

Vamos fazer as seguintes considerações:

Condução de calor unidimensional;
Condução transiente;
Propriedades constantes;
Não há geração térmica.

Assim, a equação de calor pode ser escrita da seguinte forma:

Para condição inicial, o problema nos disse que:

Como condições de contorno, o problema nos disse que a superfície em troca calor por convecção e a superfície em é mantida à temperatura constante .

Assim:

Passo 2

Solução analítica.

Para encontrar a solução analítica, vamos partir do princípio que o problema possui uma solução homogênea (a qual vamos calcular a partir das soluções tabeladas) e uma solução particular (não-homogênea, que teremos que resolver), que depende somente de .

Assim:

Aplicando isso à nossa formulação matemática, teremos:

Separando os dois problemas, teremos:

Passo 3

Começando pela solução homogênea:

Pelas condições de contorno, este corresponde ao caso 7 da nossa tabela, onde:

Sendo as raízes da seguinte expressão:

Sendo . Assim, a solução homogênea será dada por:

Agora é arrumar a casa:

Vamos resolver essa integral separadamente:

Finalmente, a solução homogênea será:

Onde é a raiz de:

A partir da expressão acima, podemos chegar à expressão de da seguinte forma:

A partir dessa expressão da tangente, podemos pensar no seguinte triângulo retângulo:

Onde:

Finalmente:

Passo 4

Para a solução particular, temos que:

Integrando uma vez a equação duas vezes, temos que:

Aplicando à primeira condição de contorno, para :

Aplicando a segunda condição de contorno, para :

Substituindo a expressão de que acabamos de encontrar:

A constante será:

Dessa forma, a solução particular será:

Passo 5

Finalmente, a solução analítica do problema será:

Substituindo as soluções:

Resposta

Exercício Resolvido #2

Questão 2, UFRJ, P1-2005.2

(Adaptado) Um chip, com base quadrada de lado e espessura , é montado em um substrato. O substrato comporta-se como um isolante ideal. O chip é resfriado por convecção forçada de ar através da sua superfície superior, que é a única não isolada pelo substrato.

A temperatura do ar é e o coeficiente de transferência de calor é . O chip encontra-se inicialmente desligado e em equilíbrio com o ar. Quando o chip é ligado, energia é gerada uniformemente em seu interior com uma taxa volumétrica .

Forneça:

Formulação matemática do problema.

Solução analítica.

Passo 1

Formulação matemática do problema.

Para chegar à formulação matemática, vamos partir da equação de calor, dada por:

Vamos fazer as seguintes considerações:

Condução de calor unidimensional;
Condução transiente;
Propriedades constantes;

Assim, a equação de calor pode ser escrita da seguinte forma:

Para condição inicial, o problema nos disse que o chip encontra-se inicialmente em equilíbrio com o ar, assim:

Como condições de contorno, o problema nos disse que uma das superfícies está termicamente isolada , e há troca de calor por convecção com o ar na outra superfície .

Assim:

Passo 2

Solução analítica.

Nós vamos dividir a solução em uma solução homogênea (que vamos calcular a partir das soluções tabeladas) e uma solução particular (não-homogênea, que teremos que resolver), que depende somente de .

Assim:

Aplicando isso à nossa formulação matemática, teremos:

Separando os dois problemas, teremos:

Passo 3

Começando pela solução homogênea:

Pelas condições de contorno, este corresponde ao caso 6 da nossa tabela, onde:

Sendo as raízes da seguinte expressão:

Sendo . Assim, a solução homogênea será dada por:

Agora é arrumar a casa:

Vamos resolver essa integral separadamente:

Finalmente, a solução homogênea será:

Onde é a raiz de:

A partir da expressão acima, podemos chegar à expressão de da seguinte forma:

A partir dessa expressão da tangente, podemos pensar no seguinte triângulo retângulo:

Onde:

Finalmente:

Passo 4

Para a solução particular, temos que:

Integrando uma vez a equação duas vezes, temos que:

Aplicando à primeira condição de contorno, para :

Assim:

Aplicando a segunda condição de contorno, para :

Substituindo a expressão de que acabamos de encontrar:

Passo 5

Finalmente, a solução analítica do problema será:

Substituindo as soluções:

Resposta

Exercício Resolvido #3

Questão 4, UFRJ, P1-2005.2

Uma placa de aço , com espessura , encontra-se inicialmente na temperatura uniforme . As duas superfícies da placa são então mantida na temperatura . Para este problema, considerando propriedades físicas constantes, forneça:

Formulação matemática;

Solução analítica;

Temperatura do centro da placa 10 minutos depois de iniciado o resfriamento.

Passo 1

Formulação matemática.

Para chegar à formulação matemática, vamos partir da equação de calor, dada por:

Vamos fazer as seguintes considerações:

Condução de calor unidimensional;
Condução transiente;
Propriedades constantes;
Não há geração térmica.

Assim, a equação de calor pode ser escrita da seguinte forma:

Para condição inicial, o problema nos disse que:

Como condições de contorno, o problema nos disse que as superfícies são mantidas a . Assim:

Passo 2

Solução analítica;

Nesse caso, como as temperaturas em ambos os lados da placa são iguais, podemos transformar esse problema em homogêneo utilizando , tal que:

Fazendo isso, a formulação matemática passa a ser dada por:

Pelas condições de contorno, este corresponde ao caso 1 da nossa tabela, onde:

Sendo as raízes da seguinte expressão:

Assim, a solução homogênea será dada por:

Agora é arrumar a casa:

Vamos resolver essa integral separadamente:

Finalmente, a solução homogênea será:

Onde é a raiz de:

O seno é nulo para qualquer múltiplo de . Assim:

Dessa forma, substituindo na expressão da solução homogênea:

Repare que, para valores pares de , e, para valores ímpares, . Assim, podemos levar somente em consideração os valores ímpares de , substituindo o na equação por . Dessa forma: