Sólido Semi-Infinito
Produzido por Giovanna RonzéTeoria
Introdução
A gente já viu como resolver problemas de condução no regime transiente pra 3 casos: parede plana, cilindro (infinito) e esfera. Agora, a gente vai tratar de um quarto caso: o sólido semi-infinito.

Calma, jovem padawan! Bora entender o que é isso! Imagina aquele dia quente de verão, você na praia curtindo as férias... Daí você resolve comprar uma água de coco lá no calçadão, só que você tá descalço!
Você vai caminhando pela areia quente, mas chega um momento em que você não aguenta mais pisar nela e sai correndo desesperado pra uma sombra mais perto nesse nível de desespero:

Pois é, demora um tempo até que o chão troque calor com você e chegue nas células que te fazem sentir dor.
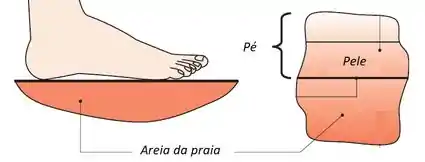
O seu pé nesse caso é um sólido semi-infinito, porque apesar do chão estar trocando calor com você, essa energia não vai chegar até a sua cabeça. A troca de calor é importante só ali naquela região do pé próxima ao chão.
Num sólido semi-infinito, a gente precisa saber o que acontece na superfície e quais as temperaturas dos corpos antes do contato. No caso do pé na areia, a gente poderia saber a temperatura da areia e a temperatura inicial do pé pra calcular o tempo necessário até sentir dor.
Como tratamos as condições na superfície?
De maneira geral, a gente tem basicamente 3 condições na superfície. Dá uma olhada:
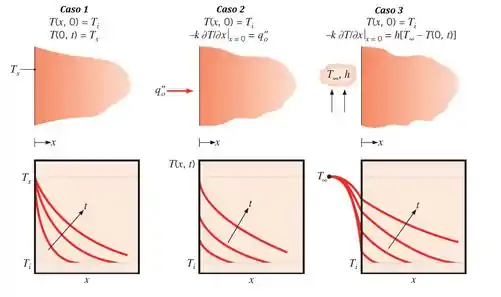
Bora ver como resolver esses casos.
Caso 1: Temperatura Constante na Superfície
Quando a gente já sabe a temperatura da superfície (), a condição de contorno é:
Com as resoluções matemáticas propostas até aqui, a gente chegou numa fórmula simples que relaciona as temperaturas do problema com o tempo, olha só:
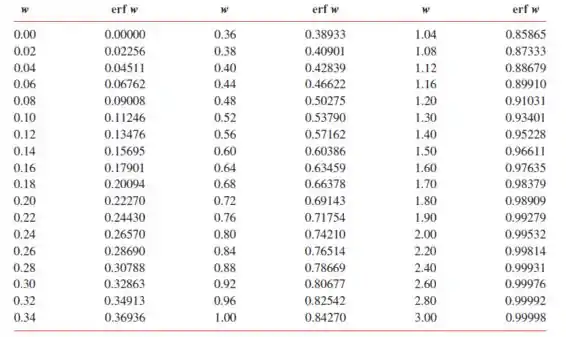
A função erro de Gauss já tá tabelada, se liga:
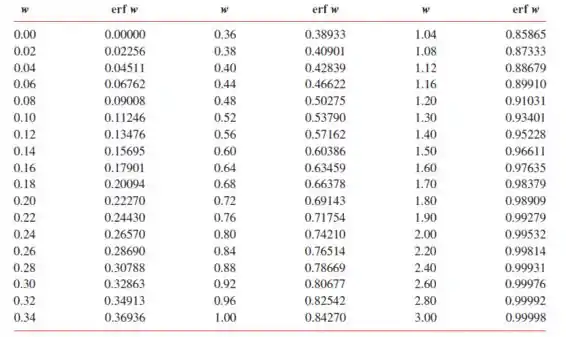
Pra usar essa tabela é fácil! Você precisa calcular o argumento da função (), olhar na coluna dos argumentos qual valor mais se aproxima e verificar o valor correspondente do !
Show! Se descobriram uma fórmula pra distribuição de temperaturas , a gente consegue calcular também o fluxo de calor. Então, chegaram à outra expressão:
Caso 2: Fluxo de calor constante na superfície
Pra esse caso aqui, a gente já sabe o valor do fluxo de energia () que é aplicado à superfície, então a gente fica com:
E a solução para a distribuição de temperatura é dada por:
Onde:
Então vamos precisar dar uma olhadinha novamente na tabela com os valores de erro de Gauss, beleza?
Caso 3: Convecção na superfície
Quando a superfície está exposta a um fluido numa dada temperatura , a condição de contorno é que a taxa de condução no sólido é igual à taxa de convecção, então:
Sendo assim, a gente fica com a seguinte solução:
Existe a possibilidade ainda da gente utilizar gráficos, ao invés da tabela. Pra isso, basta a gente calcular as duas coordenadas ( ou ) e ver de qual curva o ponto está mais próximo ou calcular uma das coordenadas e identificar a curva pra determinar qual a outra coordenada.
Dá uma olhada na cara do gráfico aqui embaixo:
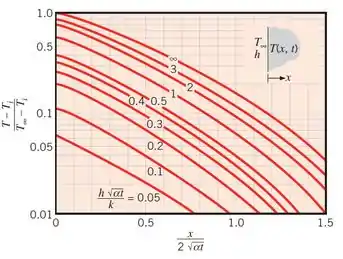
Pra isso, temos que calcular a razão:
Contato entre dois sólidos semi-infinitos
Ao colocarmos em contato dois sólidos semi-infinitos, partindo do princípio que o contato é perfeito (resistência térmica de contato desprezível), será atingida instantaneamente a igualdade de temperatura na superfície de contato, como mostrado abaixo:
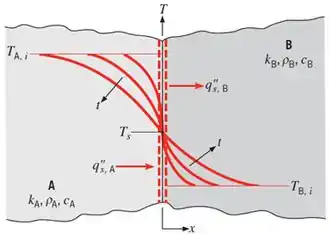
Se ambos possuírem o mesmo material, a temperatura na superfície será a média aritmética das temperaturas:
Caso os corpos possuam materiais diferentes, a temperatura da superfície é calculada a partir do fluxo de calor que calculamos no caso 1, se liga:
Reorganizando essa equação, encontraremos o seguinte:
Agora que já vimos o que é um sólido semi-infinito e como resolvemos problemas, bora aos exercícios!
Como tratamos as condições na superfície?
Caso 1: Temperatura Constante na Superfície
Caso 2: Fluxo de calor constante na superfície
Caso 3: Convecção na superfície
Contato entre dois sólidos semi-infinitos
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Um bloco espesso de madeira ( e pintado de preto a é submetido a um fluxo de calor solar constante de .
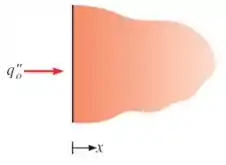
Determine a temperatura da superfície exposta do bloco após .
Qual seria a sua resposta se o bloco fosse feito de alumínio?
Dados referentes ao alumínio: e .
Passo 1
Determine a temperatura da superfície exposta do bloco após .
Esse é um problema de condução transiente em um meio semi-infinito submetido a um fluxo de calor constante na superfície, ou seja, é o nosso Caso 2. A gente já viu que existe uma expressão para a temperatura para esse tipo de situação:
O enunciado pede pra gente avaliar a superfície do bloco exposta, então :
Como exponencial de é :
E dando uma olhada lá na tabela da função erro complementar (), descobrimos que . Então:
Já ficou com uma carinha melhor né?
Passo 2
Pra avaliar o bloco de madeira após , a gente tem que passar esses para segundos. E chegamos no seguinte:
Passo 3
Qual seria a sua resposta se o bloco fosse feito de alumínio?
Caso o bloco fosse de alumínio, a gente teria difusividade () e condutividade () térmicas diferentes! Mas, como continuamos avaliando a superfície exposta, temos que . Logo:
Após , a temperatura da superfície seria:
Ou seja, com o mesmo fluxo de calor, a superfície de um bloco de alumínio permaneceria a uma temperatura menor do que a de um bloco de madeira.
Isso acontece porque o alumínio conduz energia térmica melhor que a madeira. Na madeira, a energia sofre uma resistência maior a migrar para o resto do sólido, acumulando-se então logo no início, o que torna a temperatura da superfície maior.
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
A massa específica e o calor específico de um material plástico são conhecidos ( e ), mas sua condutividade térmica é desconhecida. Para determinar a condutividade térmica, uma experiência é realizada, na qual uma amostra fina de um material é aquecida a uma temperatura uniforme de e então resfriada pela passagem de ar a sobre uma superfície. Um termopar fixado a uma distância de abaixo da superfície registra a resposta térmica do plástico durante o resfriamento.
Se o coeficiente de convecção associado com a corrente de ar é e a temperatura é registrada após iniciar o resfriamento, qual é a condutividade térmica do material?
Passo 1
A gente pode ilustrar o enunciado da seguinte maneira:
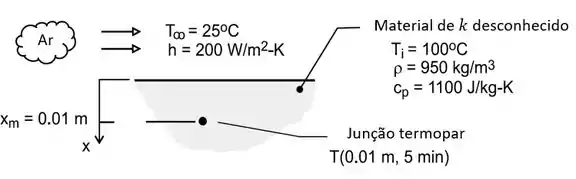
Esse caso trata de convecção numa superfície, logo estamos falando do Caso 3. A gente já viu que existe uma expressão pronta para a razão entre temperaturas:
Note que a condutividade térmica () só aparece dentro da definição de difusividade térmica () na expressão acima. Sendo assim, a gente precisa abrir a expressão de :
Mas é uma equação implícita! Ou a gente resolve por um método numérico (como Newton-Raphson ou Bisseção), ou a gente resolve com uma calculadora científica! Mais fácil pegar uma HP então!
Passo 2
Como a gente já sabe a temperatura inicial () e final () e a temperatura do fluido (), bora calcular o valor da razão:
Passo 3
Então, temos que:
Substituindo os seguintes valores do enunciado para resolver na HP:
Sendo assim, a gente fica com:
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Pavimentos asfálticos podem atingir temperaturas acima de em dias quentes de verão. Considere que tal temperatura exista em todo o pavimento, quando subitamente uma tempestade reduz a temperatura da superfície para . Calcule a quantidade total de energia (por unidade de área) que será transferida do asfalto em um período de no qual a superfície é mantida a . As propriedades termofísicas do asfalto são , e .
Passo 1
Esse caso trata de uma superfície com temperatura constante, logo estamos falando do Caso 1. A gente já viu que existe uma expressão pronta para o fluxo de calor nessa condição, que é dada por:
Esse fluxo varia ao longo do tempo, como a gente pode perceber. Então, pra gente encontrar a quantidade total de energia que será transferida do asfalto, basta a gente integrar essa expressão ao longo do tempo:
Substituindo a expressão do fluxo:
Integrando a expressão:
Passo 2
Bora calcular a difusividade térmica () então:
Substituindo os valores do enunciado:
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
(Adaptada) Uma placa fina de aço (, e ) está inicialmente a e é resfriada por um jato de água colidindo em uma de suas superfícies. A temperatura da água é de e o jato mantém um coeficiente de convecção na superfície elevado e aproximadamente uniforme. Considerando que a superfície é mantida à temperatura da água através do resfriamento, quanto tempo levará para a temperatura alcançar a uma distância de da superfície?
Dica: Assuma que a derivada da função em relação ao coeficiente de convecção () é sempre maior que a derivada da função .
Passo 1
A gente pode ilustrar o enunciado da seguinte maneira:
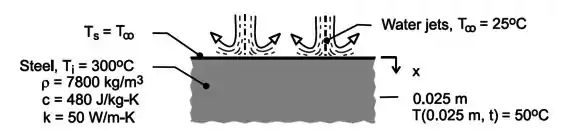
Esse caso trata de convecção numa superfície, logo estamos falando do Caso 3. A gente já viu que existe uma expressão pronta para a razão entre temperaturas:
No enunciado tá escrito que “o jato mantém um coeficiente de convecção na superfície elevado”. Ou seja, seu valor é muito alto! Podemos então analisar a equação quando o tende ao infinito ()!
Note que o primeiro termo não depende de , mas o segundo sim! Então bora analisar primeiro a exponencial e depois a função !
Passo 2
Analisando o termo exponencial:
Analisando o termo gaussiano:
Sendo assim, a gente pode verificar pela regra de L’Hospital a razão:
O limite quando dá a indeterminação e, então, a gente pode derivar em cima e em baixo:
Aí é que vem a dica! Como a derivada da função exponencial em relação ao coeficiente é sempre menor que a derivada da função , a razão vai a zero quando . Dessa forma, a gente fica com:
Passo 3
Como a gente já sabe a temperatura inicial () e final () e a temperatura do fluido (), bora calcular o valor da razão:
Passo 4
Então, temos que:
Pela tabela, temos que o argumento da função erro complementar será aproximadamente:
Isolando o termo do tempo:
Bora, então, calcular a difusividade térmica () do material:
Substituindo os valores do enunciado:
Resposta
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Padrões para paredes contrafogo podem ser baseados em suas respostas térmicas a um fluxo térmico radiante especificado. Seja uma parede de concreto com de espessura (, e ), que se encontra a uma temperatura inicial de e é irradiada em uma superfície por lâmpadas que fornecem um fluxo térmico uniforme de . A absortividade da superfície em relação à radiação é . Se as exigências de construção ditam que as temperaturas nas superfícies irradiada e não-irradiada, após de aquecimento, não podem exceder e , respectivamente, as exigências serão atendidas?
Passo 1
A gente pode entender o enunciado com a seguinte ilustração:
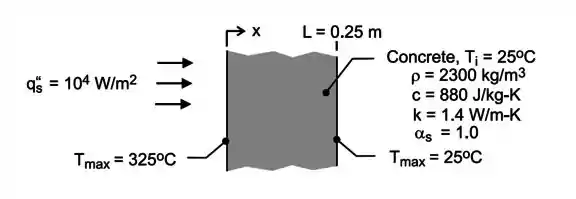
Nessa situação, temos um fluxo de calor constante na superfície de valor conhecido (). Sendo assim, a gente está no Caso 2 e temos uma expressão pronta para determinar a temperatura em algum ponto do material:
Passo 2
Bora, primeiro, calcular a difusividade térmica () do material:
A gente precisa calcular a temperatura das duas superfícies após : em e em . Mas antes bora calcular o termo que é constante nas duas situações:
Vamos agora determinar a temperatura em cada superfície após 30 minutos.
Passo 3
- No instante de em :
- No instante de em :
Assim:
Como é menor que o limite de , a condição ainda é satisfeita após para a parede na posição .
Passo 4
Substituindo os demais valores:
Assim:
Pela tabela:
Podemos ainda escrevero como sendo :
Assim, ficamos com:
Como é menor que o limite de , a condição ainda é satisfeita após para a parede na posição .
Resposta
Ambas as condições são satisfeitas, porque as temperaturas nas superfícies, após são de:
Exercício Resolvido #6
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Um ferro para soltar cerâmica consiste em uma placa maciça mantida a por um aquecedor elétrico incorporado. O ferro é colocado em contato com uma cerâmica para promover o amolecimento do adesivo, permitindo que a cerâmica seja levantada facilmente da base na qual ela se encontra fixada. O adesivo irá amolecer suficientemente se aquecido acima de por um tempo mínimo de , mas sua temperatura não deve exceder para evitar deterioração do adesivo.
Considere a cerâmica e a base de fixação com temperatura inicial de e propriedades termofísicas equivalentes a: e .
Quanto tempo levará um trabalhador usando tal dispositivo para suspender a cerâmica?
A temperatura do adesivo irá exceder ?
Se o dispositivo tem área superficial quadrada de de lado, qual a quantidade de energia é removida do mesmo durante o tempo que leva para suspender a cerâmica?
Passo 1
Quanto tempo levará um trabalhador usando tal dispositivo para suspender a cerâmica?
Esse caso trata de uma superfície com temperatura constante, logo estamos falando do Caso 1.
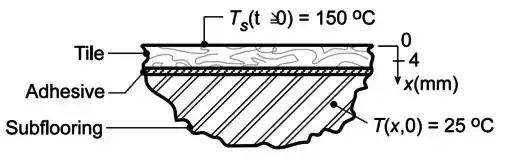
A gente já viu que existe uma expressão pronta para a razão entre as temperaturas nessa condição, que é dada por:
Bora então calcular a difusividade térmica () do material:
Sendo assim, considerando que a superfície tem que atingir , temos que:
Pela tabela o argumento da função erro que gera aproximadamente o resultado vale 0,92. Então:
Passo 2
A temperatura do adesivo irá exceder ?
Depois que a temperatura alcançar os , ela deve permanecer por, no mínimo . Então, a gente tem que avaliar qual a temperatura da superfície depois do tempo total :
Utilizando novamente a equação para o Caso 1, mas agora usando o tempo pra calcular a temperatura, teremos:
Pela tabela:
Isso equivale a , ou seja, a temperatura não ultrapassa o limite de após o tempo total.
Passo 3
Se o dispositivo tem área superficial quadrada de de lado, qual a quantidade de energia é removida do mesmo durante o tempo que leva para suspender a cerâmica?
O fluxo de energia térmica nessa condição do Caso 1 é dado pela seguinte equação:
Esse fluxo varia ao longo do tempo, como vemos na equação. Então, pra gente encontrar a quantidade total de energia que será transferida do asfalto, basta a gente integrar essa expressão ao longo do tempo:
Substituindo a expressão do fluxo:
Integrando a expressão:
Já calculamos o valor da difusividade térmica (), então: