Método dos Efeitos Espaciais
Produzido por Giovanna RonzéTeoria
Condução Transiente Unidimensional
Fala, meu show! A gente já aprendeu como aplicar o Método dos Parâmetros Concentrados, mas e quando aquela regrinha de não rolar?

A ideia aqui é a seguinte. Como não temos como aplicar o método dos parâmetros concentrados, vamos ter que partir da Equação de Calor, dada por:
O método dos efeitos espaciais se dá justamente pela solução da equação de calor. Ao resolvê-la, vamos ter uma solução aproximada que vamos poder utilizar para os casos em que .
Vamos ver aqui umas expressões bem feias, mas não se preocupe, logo à frente vamos ver como algumas soluções aproximadas facilitam um pouco a nossa vida.
Vamos considerar o caso abaixo:
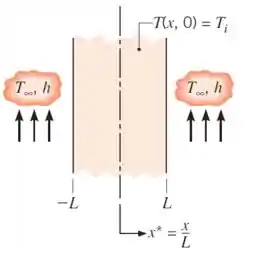
Para resolver a equação de calor, vamos adotar aqui as seguintes simplificações:
- Transferência de calor unidimensional;
- Transferência de calor sem geração térmica ;
- Propriedades térmicas constantes.
Dessa forma, a nossa equação de calor fica com essa cara:
Em que é a difusividade térmica do material.
Nesse caso, as condições de contorno que utilizaremos serão:
E a nossa condição inicial é dada por .
Adimensionalizando a Equação de Calor
Pra simplificar a equação, a gente vai diminuir o número de variáveis.
“Mas como?”
Muito boa a sua pergunta! Gosto assim! Pra isso, a gente pode propor algumas mudanças de variáveis, como a temperatura adimensional (), a distância adimensional () e o número de Fourier (), dados por:
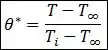
![]()
![]()
Assim, a equação do calor em coordenadas cartesianas fica com essa cara:
![]()
As nossas condições de contorno passarão a ser dadas por:
E a nossa condição inicial é dada por .
Repare que a tomou o lugar da temperatura , a distância adimensional entrou no lugar de e, por último e não menos importante, o número de Fourier passa a desempenhar o papel do tempo na forma como formulamos o nosso problema.
“Mas, e aí?! Como a gente faz pra resolver isso?!”
Hoje você está demais, hein!
A solução exata desse problema pode ser encontrada se utilizarmos o método de separação de variáveis.
Isso significa dizer que é o produto de uma função puramente de com outra função de , ou seja:
Se nós fizermos isso, substituindo na Equação de Calor, e aplicando as condições inicial de contorno, encontraremos a seguinte série infinita:
Em que:
E os valores de são as soluções da equação implícita:
Tá... provavelmente a sua expressão ao ver isso pela primeira vez foi (pelo menos a foi exatamente essa):

RELAXA! Lembra do que eu te disse lá no começo?! Embora as expressões fiquem feias, nós vamos utilizar apenas soluções aproximadas. Dessa forma, vamos utilizar apenas o primeiro termo da série, dado por:
![]()
Onde os valores de e já se encontram tabelados pra cada valor de ! Vou colocar essa tabela no final desse capítulo. Então, o que você tem que fazer é o seguinte:
- Calcular o ;
- Olhar na tabelas os respectivos valores de e (A tabela tá lá no finalzinho dessa teoria ^^);
- Ser feliz!
Solução para Cilindro Infinito
De maneira parecida com o que a gente fez para a parede plana, a gente também pode propor novas variáveis para a equação do calor em coordenadas cilíndrica, ficando com o seguinte:
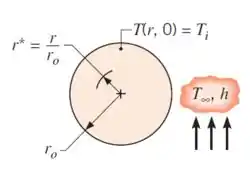
Novamente, resolvendo a Equação de Calor, e aplicando a condição inicial e as de contorno, encontraremos que a solução dessa equação também é uma série infinita, dada por:
Em que:
E os valores de são as soluções da equação implícita:
Se a gente truncar a série infinita no primeiro termo, a gente fica com a solução aproximada:
![]()
Os valores de e estão na mesma tabela (que eu vou colocar lá no final), só que na coluna dos cilindros infinitos!
Caso estejamos interessados em calcular temperatura na linha de centro , teremos:
Esse é a função de Bessel de primeira ordem. Mas não tem o que se preocupar também! Esse valor também tem uma tabela própria. Você calcula o seu argumento () e olha na tabela (que está no final dessa teoria) qual o valor de .
Solução para Esfera
Com a esfera também não poderia ser diferente, a gente fica com uma equação desse tipo:
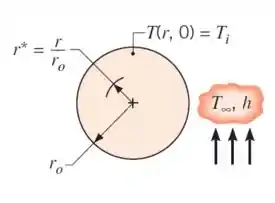
Com as mesmas condições de contorno e inicial, a solução do caso com esferas é a série abaixo:
Em que:
E os valores de são as soluções da equação implícita:
Truncando a série infinita no primeiro termo, a solução aproximada é essa daqui:
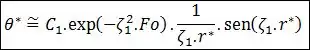
Quantidade de Calor Transferida
Em muitos casos a nossa preocupação é justamente calcular a taxa de transferência de calor. Essa taxa é calculada através do balanço de energia no corpo. Mas eu vou te colocar de cara pro gol aqui.
- Parede Plana:
- Cilindro Infinito:
- Esfera:
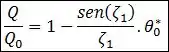
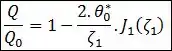
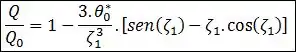
Onde é a taxa de transferência de calor no instante inicial , dada por:
Prontinho! Agora estamos mais do que prontos pra luta!
Promessa é dívida...
Conforme combinado, segue abaixo as tabelas necessárias pra resolver problemas condução transiente utilizando o método dos efeitos espaciais.
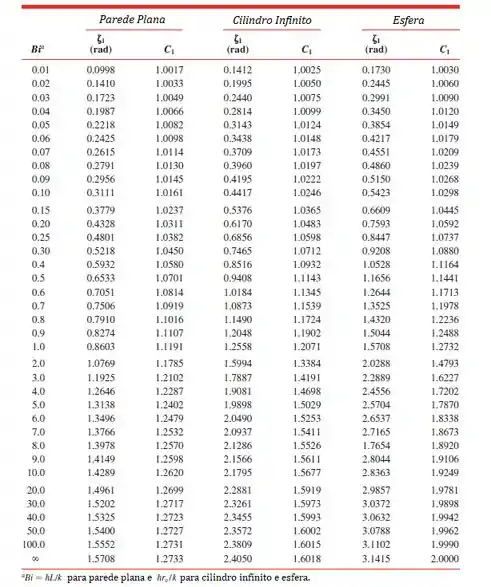
Atenção! Note no rodapé da tabela que, pra usá-la, o deve ser calculado para cilindros e esferas necessariamente por meio de:
![]()
Não dê mole com isso! Sério, nunca te pedi nada! :)
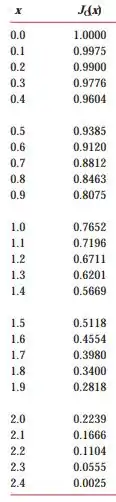
Ah! Como eu havia prometido também, a tabela abaixo mostra os valores para a função de Bessel de primeira ordem.
Adimensionalizando a Equação de Calor
“Mas, e aí?! Como a gente faz pra resolver isso?!”
Solução para Cilindro Infinito
Solução para Esfera
Quantidade de Calor Transferida
Promessa é dívida...
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Um armazenamento de energia térmica consiste em um grande canal retangular no qual é bem isolado em sua superfície externa e engloba camadas alternadas de material de armazenagem e canal de escoamento.
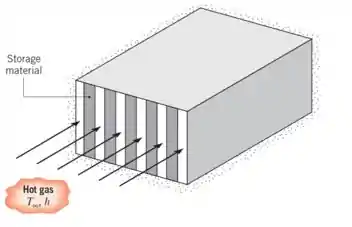
Cada camada do material de armazenamento é uma placa de alvenaria (, e ) de largura , a qual está a uma temperatura de . Considere condições para as quais a unidade de armazenamento é carregada pela passagem de um gás quente através dos canais. A temperatura do gás e o coeficiente de convecção são considerados valores constantes de e em todo o canal.
- Quanto tempo levará para atingir 75% da energia máxima possível armazenada?
- Quais são as temperaturas máxima e mínima da alvenaria nesse instante?
Passo 1
a) A situação exposta pelo enunciado pode ser vista da seguinte forma:
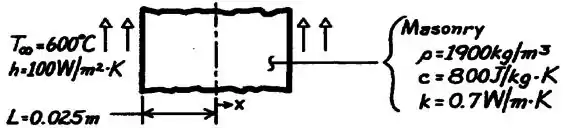
A primeira coisa que temos que fazer é calcular o número de Biot, então bora lá:
Substituindo os dados:
Como o , a gente não pode desprezar os gradientes de temperatura no interior do sólido e precisamos usar o Método dos Efeitos Espaciais!
Passo 2
Sabemos que a energia máxima (no instante ) a ser trocada é dada por:
Para o caso de paredes planas, a gente pode escrever:
Temos que encontrar o tempo no qual a razão equivale a:
Ou seja:
Substituindo a expressão da temperatura adimensional (), a gente fica com:
Em que:
A difusividade térmica () é dada por:
Assim, o número de Fourier () será:
Passo 3
Pela tabela de valores de e , a gente pode fazer uma interpolação para encontrar esses valores para o caso em que ! Bora lá então:
- Cálculo de :
- Cálculo de :
Passo 4
Substituindo a expressão para o número de Fourier e os valores das constantes, a gente tem que:
Assim:
Isso equivale a aproximadamente .
Passo 5
b) Agora a gente precisa determinar as temperaturas máxima e mínima no sólido! O sólido está esquentando, devido à convecção com o fluido pela superfície. Então, num dado instante, a gente espera que a temperatura máxima seja na parede e a mínima no centro.
Então a gente precisa calcular a temperatura em duas regiões: em (no centro) e em (na parede)! A temperatura adimensional no caso de parede plana é aproximadamente:
Substituindo as constantes:
Passo 6
A temperatura mínima () será:
Isolando a temperatura de interesse:
A temperatura máxima () será:
Isolando a temperatura de interesse:
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Em um processo de têmpera, uma lâmina de vidro que se encontra inicialmente a uma temperatura é subitamente resfriada pela redução da temperatura em ambas as superfícies para .
A lâmina tem uma espessura de e o vidro possui uma difusividade térmica de .
Quanto tempo levará até que a temperatura no plano central da lâmina atinja da sua máxima redução de temperatura possível?
Se , qual é o máximo gradiente de temperatura no vidro no instante de tempo supracitado?
Passo 1
O primeiro passo aqui é calcular o danado do Biot:
Opa! Mas o problema não nos deu o coeficiente de transferência de calor por convecção!
“E agora, José?!”
A ideia é a seguinte, quando o problema nos diz que a temperatura na superfície após o resfriamento é , é a mesma coisa que ele nos dizer que, após o resfriamento, , ou seja, seria como considerarmos .
Nesse caso, seria o mesmo que dizer que . Bom, isso definitivamente é maior do que . Kkkk Então partiu Métodos dos Efeitos Espaciais.
Passo 2
Quanto tempo levará até que a temperatura no plano central da lâmina atinja da sua máxima redução de temperatura possível?
Ok! Como não temos exatamente, o valor de Biot, não temos como utilizar a nossa tabela. Então vamos recorrer à definição dos parâmetros e .
Passo 3
Show de bola! Como estamos querendo calcular o tempo, vamos calcular o número de Fourier através da seguinte fórmula:
Como estamos calculando esse tempo no eixo central, . Dessa forma:
Como queremos saber o tempo que levará até que a temperatura no plano central da lâmina atinja da sua máxima redução de temperatura possível, devemos considerar . Dessa forma:
Utilizando a definição do número de Fourier:
Passo 4
Se , qual é o máximo gradiente de temperatura no vidro no instante de tempo supracitado?
Como queremos calcular o gradiente de temperatura, estamos querendo calcular a grandeza .
Pra isso, precisamos calcular a expressão da temperatura. A temperatura adimensional é dada por:
Derivando a expressão acima:
Sendo .
Substituindo na expressão do gradiente de temperatura:
Como queremos o máximo valor do gradiente de temperatura, basta fazer e , logo:
Substituindo os valores:
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Inicia-se a aplicação de um revestimento plástico em painéis de madeira pela deposição de polímero fundido sobre o painel e o posterior resfriamento da superfície do polímero ao submetê-la a uma corrente de ar de .
Como uma primeira aproximação, o calor de reação associado à solidificação do polímero pode ser desprezado e a interface polímero/madeira pode ser considerada adiabática.
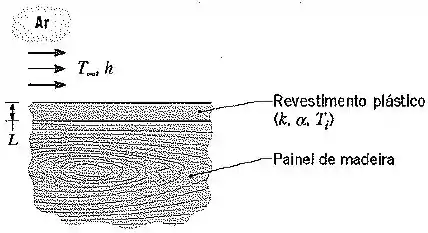
Sendo a espessura do revestimento e ele estando a uma temperatura inicial de , quanto tempo é necessário para a superfície atingir a temperatura segura para o toque de , se o coeficiente de transferência de calor por convecção for ?
Qual é o valor correspondente da temperatura na interface?
A condutividade térmica e a difusividade térmica do plástico são e , respectivamente.
Passo 1
Partiu calcular o número de Biot para essa situação:
Onde:
Substituindo os valores:
Opa! Não podemos usar o Método dos Parâmetros Concentrados aqui, então utilizaremos o Método dos Efeitos Espaciais.
Passo 2
Pelo Método dos Efeitos Espaciais, a temperatura adimensional é dada por:
Onde:
O nosso trabalho agora é encontrar os valores de e . Pra isso, vamos precisar de uma tabela (que provavelmente está no final do seu livro).
Passo 3
Pela Tabela, vemos que o valor de Biot que calculamos está entre dois valores tabela:
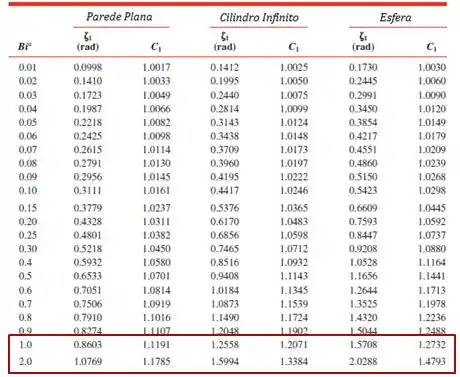
Pra encontrarmos os valores dos parâmetros que precisamos, vamos fazer uma interpolação linear aqui, beleza?
Essa interpolação pode ser feita direto na sua calculadora científica, mas se você for mais hardcore, podemos calcular os parâmetros no braço mesmo:
Utilizando os valores da tabela, encontraremos:
Passo 4
Voltando à equação da temperatura adimensional e substituindo os valores dos parâmetros que acabamos de calcular:
Onde:
Logo:
Sendo , reorganizando a equação acima, o número de Fourier será dado por:
Por definição, o número de Fourier é dado por:
Assim, o tempo necessário para que se atinja a temperatura de será:
Passo 5
Para encontrar a temperatura na interface, basta utilizar a equação para a temperatura adimensional, considerando . Dessa forma:
Sendo :
Substituindo os valores das temperaturas:
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Um longo bastão de plástico com de diâmetro e é aquecido uniformemente em uma estufa como preparação para uma operação de prensagem. Para obtenção de melhores resultados, a temperatura no bastão não deve ser inferior a .
Até que temperatura uniforme o bastão deve ser aquecido na estufa se, para o pior dos casos, o bastão repousa sobre uma esteira transportadora por antes da prensagem, permanecendo exposto a um resfriamento por convecção ao ar ambiente a , com um coeficiente convectivo de ?
Uma outra condição para a obtenção de bons resultados é a diferença entre as temperaturas máxima e mínima no bastão, que não deve exceder .
Essa condição é satisfeita e, se não, o que você poderia fazer para satisfazê-la?
Passo 1
Logo de cara vamos calcular o número de Biot para o cilindro:
Onde:
Substituindo os valores:
Logo, vamos utilizar o Método dos Efeitos Espaciais pra resolver esse problema.
Passo 2
A temperatura adimensional para o caso do cilindro é dada por:
Vamos agora determinar os valores dos parâmetros que estão faltando na equação.
Para pegar os valores de e da tabela, temos que calcular Biot da seguinte forma:
Como já temos o valor do número de Biot, podemos pegar e direto da tabela. Dessa forma:
Além disso, como o problema já nos deu o tempo que o bastão fica na estufa, podemos calcular o número de Fourier :
Substituindo os valores:
A função de Bessel de primeira ordem é dada em uma tabela a partir dos valores de e . Dado que estamos preocupados com a temperatura na superfície, . Como já calculamos o valor de , teremos:
Na tabela, vemos que esse valor está entre e .
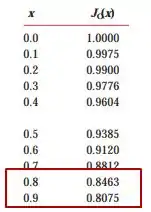
Fazendo uma interpolação linear, encontramos que .
Finalmente, substituindo todos os valores na expressão da temperatura adimensional:
Passo 3
Pra calcular a temperatura inicial do bastão, basta utilizar a definição da temperatura adimensional :
Substituindo os valores:
Passo 4
Vamos utilizar agora a condição de que a diferença entre as temperaturas máxima e mínima no bastão, que não deve exceder .
A máxima temperatura no bastão será a sua temperatura no eixo central. Dessa forma, é mais jogo usarmos essa expressão da temperatura adimensional:
Substituindo os valores:
Assim, a diferença entre as temperaturas máxima e mínima será:
Assim, a condição não é atingida.
Resposta
A condição de que a diferença entre as temperaturas máxima e mínima no bastão, que não deve exceder não é atingida.
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Como parte de um processo de tratamento térmico, bastões de aço inoxidável 304 com de diâmetro são resfriados a partir de um temperatura inicial de pela sua suspensão em um banho de óleo a .
Se um coeficiente de transferência de calor por convecção de for mantido pela circulação do óleo, quanto tempo demora para o eixo central dos bastões atingir uma temperatura de , quando então ele é retirado do banho?
Se 10 bastões de comprimento forem processados por hora, qual é a taxa nominal na qual energia deve ser retirada do banho (a carga de resfriamento)?
Passo 1
Logo de cara, precisamos calcular o número de Biot pra saber se podemos usar o Método dos Parâmetros Concentrados, mas o problema não nos deu todos os dados. E agora?!
Nesse caso, a gente costuma buscar os dados no final do livro (provavelmente em um dos apêndices). De acordo com a tabela A.1 do Incropera, para o aço inoxidável 304, temos:
Dessa forma:
Onde:
Substituindo dos valores:
Dessa forma, vamos usar o Método dos Efeitos Espaciais.
Passo 2
Um detalhe importante aqui é que, para pegarmos os valores tabelados de e temos que calcular Biot da seguinte forma:
Olhando na tabela:
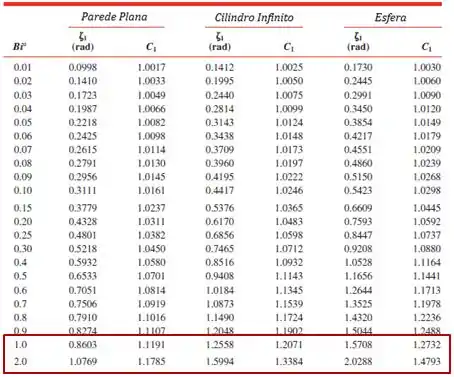
Fazendo uma interpolação linear:
Como estamos preocupados com a região central do bastão, , logo:
Sendo , , e :
Passo 3
Reorganizando os termos dessa equação:
Utilizando a definição do número de Fourier:
Substituindo os valores:
Passo 4
A quantidade de calor transferida é dada por:
Onde é a quantidade de calor transferida inicialmente, dada por:
Onde:
Substituindo todos os valores:
Passo 5
No entanto, essa é a energia transferida por cada bastão.
A taxa total nominal de energia transferida pelos 10 bastões será dada por:
Resposta
Exercício Resolvido #6
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
(Adaptada) Uma câmara de ar frio é proposta para o resfriamento de esferas de aço de rolamento com diâmetro e temperatura inicial . O ar na câmara é mantido a por meio de um sistema de refrigeração e as esferas de aço passam através da câmara em uma esteira transportadora. A produção ótima de rolamentos exige que da energia térmica inicial contida na esfera acima de sejam removidas. Efeitos de radiação pode ser desprezados e o coeficiente de transferência de calor por convecção dentro da câmara é de .
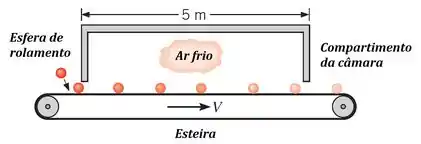
Calcule o tempo de resistência das bolas no interior da câmara.
Estime a velocidade da esteira transportadora, a fim de atender à exigência de operação.
As seguintes propriedades podem ser usadas para o aço: , e .
Passo 1
Calcule o tempo de resistência das bolas no interior da câmara.
As esferas individualmente são como mostrado abaixo:
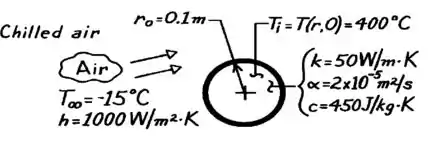
A gente vai analisar uma única esfera logo no começo do equipamento. Então, bora ver se a gente pode usar o Método dos Parâmetros Concentrados nesse problema pelo número de Biot:
O comprimento característico () pela razão entre volume e área da esfera é calculado por:
Pela distância que corresponde a maior diferença de temperatura, a gente tem que:
Como o fica menor usando a primeira opção, bora usar ele, porque assim fica mais fácil da aproximação do método dos parâmetros concentrados valer ^^
Assim:
É, não adiantou! Como , a gente não pode usar o Método dos Parâmetros Concentrados! Então, a gente precisa do Método dos Efeitos Espaciais!
Passo 2
Para o caso das esferas sólidas, a gente tem que:
O enunciado afirma que aquelas esferas cuja razão seja de serão removidas, então esse será o critério pra saber quanto tempo elas ficarão lá dentro! Sendo assim:
Pela tabela, conseguimos encontrar as constantes e ! Mas aqui você tem que ter muito cuidado! No finalzinho da tabela com as constantes, tem escrito como que o número de Biot deve ser calculado!
A gente já calculou o número de Biot pra saber se poderíamos usar o Método dos Parâmetros Concentrados. Pra isso, a gente pode escolher como calcular. Mas pra usar a tabela, o número de Biot deve ser calculado da seguinte forma:
Com esse valor de , a gente não precisa interpolar! Temos direto da tabela que:
Substituindo na equação as constantes, a gente fica com:
Passo 3
Além disso, a temperatura adimensional no centro do sólido () é dada por:
Vemos que dá uma indeterminação , logo podemos aplicar o teorema de L’Hospital, derivando numerador e denominador pra tirar novamente o limite:
Em que:
Assim, o número de Fourier () será:
Logo:
Passo 4
Substituindo na equação as constantes e o valor de , a gente fica com:
Isso equivale a aproximadamente !
Passo 5
Estime a velocidade da esteira transportadora, a fim de atender à exigência de operação.
Como a esteira tem de comprimento, como indicado na figura, e o tempo necessário para a esfera ficar no sistema é de , esperamos que a velocidade da esteira seja:
Resposta
Exercício Resolvido #7
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Sistemas de armazenamento de energia térmica em geral envolvem um leito de esferas sólidas, através do qual um gás quente escoa se o sistema está sendo carregado ou um gás frio se o sistema está sendo descarregado. No processo de carregamento, o calor transferido do gás quente aumenta a energia térmica armazenada dentro das esferas frias; durante a descarga, a energia diminui conforme o calor é transferido das esferas aquecidas para o gás refrigerante.
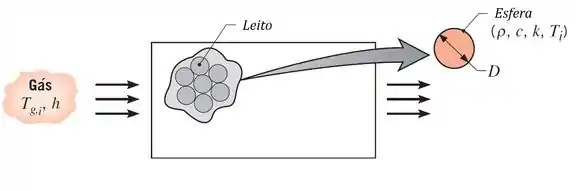
Considere o leito com esferas de pirex (, e ) de 75 mm de diâmetro e o processo de carregamento, para o qual o gás entra na unidade de armazenamento à temperatura de .
Se a temperatura inicial das esferas é de e o coeficiente de convecção é , quanto tempo levará a esfera próxima à entrada do sistema para acumular 90% da máxima energia térmica possível?
Qual a temperatura no centro da esfera?
Passo 1
Se a temperatura inicial das esferas é de e o coeficiente de convecção é , quanto tempo levará a esfera próxima à entrada do sistema para acumular 90% da máxima energia térmica possível?
A situação proposta pode ser ilustrada de maneira simplificada da seguinte forma:
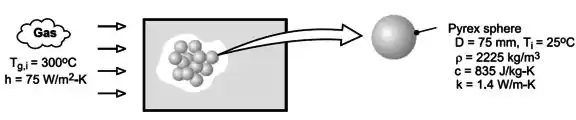
A gente vai analisar uma única esfera logo no começo do equipamento. Então, bora ver se a gente pode usar o Método da Capacidade Concentrada nesse problema pelo número de Biot:
O comprimento característico () pela razão entre volume e área da esfera é calculado por:
Pela distância que corresponde a maior diferença de temperatura, a gente tem que:
Como o fica menor usando a primeira opção, bora usar ele, porque assim fica mais fácil da aproximação do método da capacidade concentrada valer ^^
Assim:
É, não adiantou! Como , a gente não pode usar o Método da Capacidade Concentrada! Então, a gente precisa do Método dos Efeitos Espaciais!
Passo 2
Para o caso de uma esfera, a razão entre as quantidades de calor é dada por:
O enunciado nos pede uma razão de , logo podemos escrever que:
Pela tabela, conseguimos encontrar as constantes e ! Mas aqui você tem que ter muito cuidado! No finalzinho da tabela com as constantes, tem escrito como que o número de Biot deve ser calculado!
A gente já calculou o número de Biot pra saber se poderíamos usar o Método da Capacidade Concentrada. Pra isso, a gente pode escolher como calcular. Mas pra usar a tabela, o número de Biot deve ser calculado da seguinte forma:
Com esse valor de , a gente não precisa interpolar! Temos direto da tabela que:
Substituindo na equação as constantes, a gente fica com:
Passo 3
Além disso, a temperatura adimensional no centro do sólido () é dada por:
Vemos que dá uma indeterminação , logo podemos aplicar o teorema de L’Hospital, derivando numerador e denominador pra tirar novamente o limite:
Em que:
A difusividade térmica () é dada por:
Assim, o número de Fourier () será:
Logo:
Passo 4
Substituindo na equação as constantes e o valor de , a gente fica com:
Isso equivale a aproximadamente !
Passo 5
Qual a temperatura no centro da esfera?
A gente sabe que a temperatura adimensional da esfera é dada por:
Então, avaliando a expressão no centro (), a gente cai no que já achamos antes pelo limite da expressão:
Com as constantes, achamos que:
Logo, pela definição de temperatura adimensional, a gente fica com:
Logo:
Resposta
Exercício Resolvido #8
Questão 3, UFRJ, P1-2007.1
Em um processo de fabricação de elementos estruturais, cilindros de aço são moldados a quente e em seguida resfriados em água. Considere um cilindro de aço ( e ) com de comprimento e de diâmetro.
O cilindro, que se encontra inicialmente na temperatura uniforme de , é resfriado em água a . O coeficiente de transferência de calor entre o cilindro e a água é de .
Calcule a temperatura no centro do cilindro 20 minutos após a imersão.
Passo 1
Esse se trata de um problema de condução em regime transiente. Assim, pra sabermos qual o método mais adequado pra resolver o problema, precisamos começar calculando o número de Biot que, no caso de um cilindro, é dado por:
Como o número de Biot é maior que 0,1, vamos usar o método dos efeitos espaciais.
Passo 2
Nesse caso, a temperatura adimensional no cilindro é aproximada por:
Como estamos interessados em calcular a temperatura na linha de centro, , e . Logo:
Onde:
De acordo com a tabela da Teoria, temos que calcular:
E para teremos, de acordo com a tabela:
Substituindo os valores:
Passo 3
A temperatura adimensional é definida por:
Substituindo os valores, teremos:
Resposta
Exercício Resolvido #9
Questão 3, UFF, 2016/2
(Adaptado) Relembrando que sua mãe em uma certa ocasião disse que a carne deve ser cozida até que cada porção tenha atingido uma temperatura de , quanto tempo levará para cozinhar de carne?
Admita que o alimento está inicialmente a e que a temperatura do forno seja de com um coeficiente de convecção de .
Considere a carne como um cilindro tendo um diâmetro igual ao seu comprimento e propriedades termofísicas dadas por: capacidade calorífica de , massa específica de , condutividade térmica de .
Passo 1
Antes de qualquer coisa, vamos determinar as dimensões dos de carne.
De acordo com o enunciado, devemos considerar a carne como um cilindro com diâmetro igual ao seu comprimento, . Assim, o comprimento da carne será:
Passo 2
Para determinar o método mais adequado pra resolver o problema, precisamos calcular o número de Biot, dado por:
Sendo assim, vamos usar o Método dos Efeitos Espaciais.
Passo 3
Nesse método, estamos considerando a variação da temperatura ao longo do corpo que estamos analisando. Como o objetivo da questão é achar o tempo em que toda a carne estará a pelo menos 80ºC, vamos calcular o tempo pro ponto mais frio da carne chegar aos 80ºC, porque assim temos certeza que todo o resto já vai estar em temperaturas maiores.
Já que a carne tá sendo aquecida por convecção na sua superfície externa, o ponto mais frio vai ser sempre o centro do cilindro.
Ótimo! Temos uma equação simplificada no método dos efeitos espaciais pro cálculo no centro de um cilindro infinito:
Dessa equação queremos calcular o número de Fourier , que é a variável adimensional do tempo, e pra isso precisamos determinar as outras variáveis adimensionais que vamos usar:
Pronto! Agora ficou faltando só usar o Biot que calculamos lá atrás, pra pegar na tabela as constantes da equação:
Passo 4
Agora que já temos tudo que precisamos, vamos reorganizar a equação em função do número de Fourier e aí é só substituir os valores que temos:
Passo 5
Por último, mas não menos importante, precisamos abrir o número de Fourier para achar o tempo:
Lembrando que o é a difusividade térmica do material, que pode ser achada em função das propriedades que o enunciado deu pra gente: