Taxa de Transferência de Calor Bidimensional
Produzido por Giovanna RonzéTeoria
Introdução
Quando estamos trabalhando em casos de condução bidimensional de calor, muitas vezes estamos interessados em calcular a taxa de transferência de calor através de um corpo, nem sempre queremos saber como é dada a distribuição de temperaturas.
Por exemplo, vamos pensar na seguinte situação: um forno cúbico para fusão de vidro possui dimensões externas de de lado e é construído com tijolos refratários, com espessura e condutividade térmica .
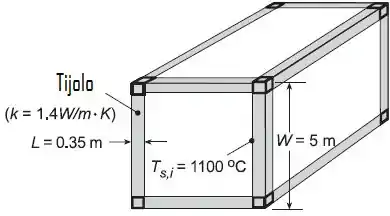
As laterais e o topo do forno estão expostos ao ar ambiente a , com a convecção natural caracterizada por um coeficiente médio . A base do forno encontra-se sobre uma plataforma, que permite exposição de uma grande parte de sua superfície ao ar ambiente, e, em uma primeira aproximação, um coeficiente convectivo de pode ser admitido.
Sob condições de operação nas quais gases de combustão mantêm as superfícies internas do forno a , qual é a perda de calor no forno?
Na teoria, teríamos que resolver a equação de calor, ver como se comporta a distribuição de temperatura no corpo e depois tratar de calcular a taxa de transferência de calor.

Mas, na real, alguém com o coração muito grande tabelou a solução para vários casos desse tipo. Basicamente, temos duas formas de calcular a taxa de transferência de calor: através do Fator de forma e da Taxa de transferência de calor adimensional.
Fator de Forma
Utilizando o Fator de Forma, podemos escrever a taxa de transferência de calor da seguinte forma:
![]()
Onde é a condutividade térmica do material, e é a diferença de temperaturas entre os contornos.
Podemos escrever, assim, a resistência térmica de condução bidimensional como sendo:
![]()
O fator de forma pode ser calculado a partir de casos tabelados que, pra não deixar muito bagunçado, vou colocar no final desse capítulo. ;)
Taxa de Condução de Calor Adimensional
Quando o objeto está imerso em um meio infinito, podemos calcular a taxa de transferência de calor através da taxa de condução de calor adimensional da seguinte forma:
![]()
Onde é a área superficial do objeto, e é o comprimento característico, definido por:
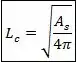
A taxa de condução adimensional também é tabelada, e pra não deixar isso bagunçado, vou colocar a tabela com as expressões para calculá-la no final do capítulo. :)
Voltando ao nosso problema...
Bom, o problema nos deu o coeficiente convectivo e nos deu as temperaturas da parede interna do forno e do ar ambiente. Nesse caso, podemos calcular a taxa de transferência de calor utilizando as resistências térmicas, da seguinte forma:
Onde a resistência térmica de convecção é dada por:
A resistência térmica de condução bidimensional é dada por:
Pra calcular o fator de forma , devemos levar em consideração:
- 8 vértices (caso 9 da tabela);
- 12 arestas (caso 8 da tabela);
- 6 faces planas (após a tabela).
Dê uma parada e procure esses casos na tabela do próximo tópico. Te espero aqui. =)
...
Beleza! Levando em consideração todos esses fatores, o fator de forma será dado por:
Onde é a área da superfície plana interna do forno, dada por . Substituindo os valores:
![]()
Assim, a resistência térmica de condução bidimensional será:
Dessa forma, a taxa de transferência de calor será:
![]()
Promessa é dívida =)
Conforme combinado, segue abaixo as tabelas pra o Fator de Forma e para a Taxa de Transferência de Calor Adimensional.
Fator de Forma :
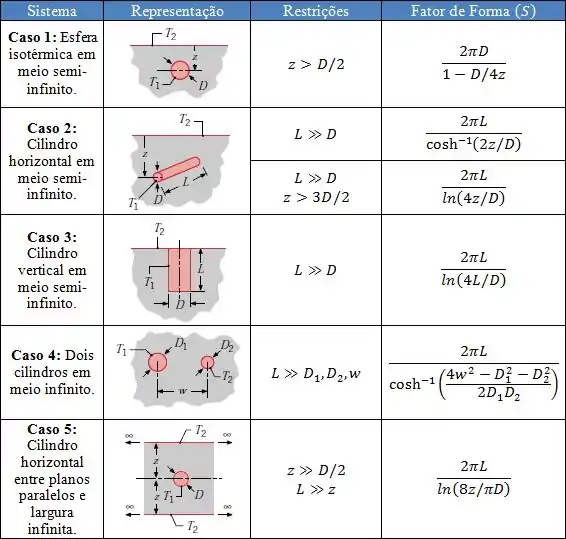
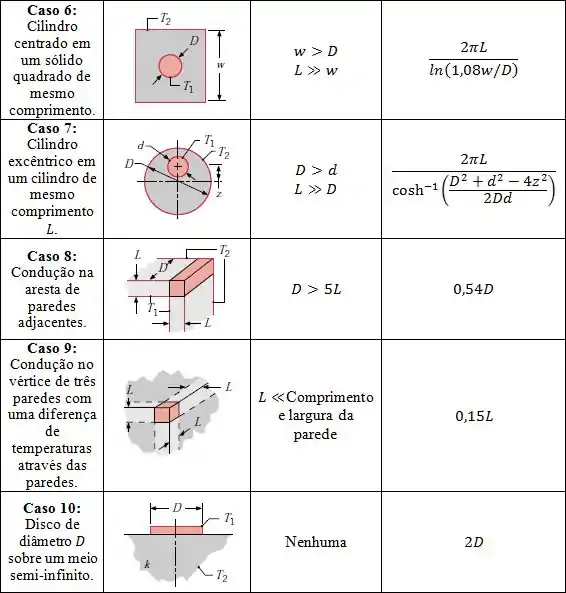
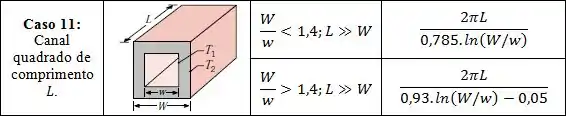
Parede plana:
Onde é a espessura da parede.
Parede cilíndrica:
Parede esférica:
Taxa de transferência de Calor Adimensional :
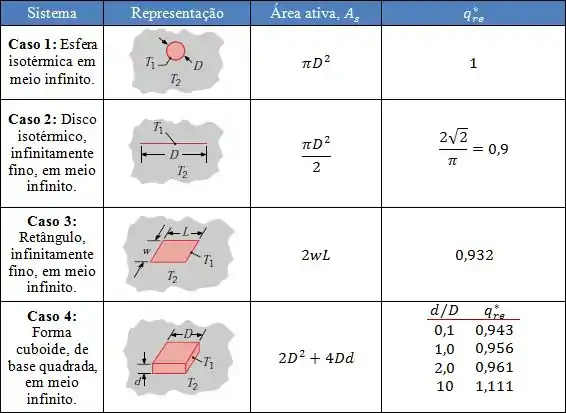
Fator de Forma S
Taxa de Condução de Calor Adimensional q r e *
Voltando ao nosso problema...
Promessa é dívida =)
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Um fluido quente escoa através de canais circulares em uma peça de ferro fundido com espessura , que apresenta um contato deficiente com as placas de cobertura , que têm espessura .
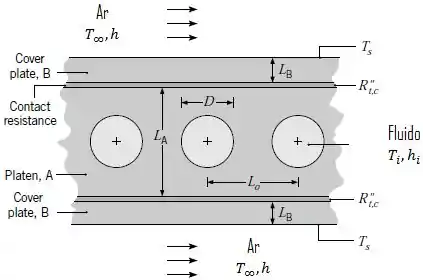
Os canais possuem diâmetro e o espaçamento entre as linhas de centro de canais adjacentes é . As condutividades térmicas dos materiais são e , enquanto a resistência de contato entre os dois materiais é de .
O fluido quente está a e o coeficiente de transferência de calor por convecção é de . O fator de forma entre um canal e a superfície superior, e a inferior, da peça é .
Determine a taxa de transferência de calor a partir de um único canal, por unidade de comprimento da peça na direção normal à página, .
Determine a temperatura da superfície externa da placa de cobertura, .
Passo 1
Determine a taxa de transferência de calor a partir de um único canal, por unidade de comprimento da peça na direção normal à página, .
Como o calor está sendo transferido tanto para a superfície superior, quanto para a inferior, podemos analisar o circuito considerando a transferência de calor entre a metade superior do duto e a superfície superior da placa.
Fazendo isso, teremos o seguinte circuito térmico:

Onde é a taxa de transferência de calor por unidade de comprimento. Estamos fazendo dessa forma porque o problema não nos forneceu a profundidade do sistema.
Além disso, o fator de forma dado pelo problema considera toda a superfície do duto. Nesse caso, como estamos considerando somente a metade superior do duto:
Dessa forma, a taxa de transferência de calor será:
Onde a resistência térmica total será a soma de todas as resistências térmicas, dadas por:
Repara que é o coeficiente de convecção do ar, que é tabelado.
Assim, a taxa de transferência de calor por unidade de comprimento será:
Repara que consideramos como , já que o problema não forneceu esse dado.
![]()
Passo 2
Determine a temperatura da superfície externa da placa de cobertura, .
Podemos calcular a temperatura superficial utilizando a taxa de transferência de calor que acabamos de calcular da seguinte forma:
Substituindo os valores:
![]()
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Um furo de diâmetro é perfurado através do centro de um bloco sólido de seção transversal quadrada com de lado. O furo atravessa o comprimento do bloco, que é de .
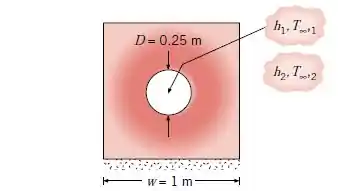
O bloco tem condutividade térmica . As superfícies externas estão expostas ao ar ambiente, com e , enquanto óleo quente escoa através do furo podendo ser caracterizado por e .
Determine a taxa de transferência de calor e as temperaturas superficiais correspondentes.
Passo 1
O calor é transferido do óleo para a superfície interna do bloco por convecção, da superfície interna para a externa por condução bidimensional, e da superfície externa do bloco para o ambiente por convecção. Assim, o circuito térmico pode ser representado por:
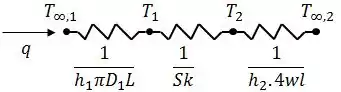
Assim, a taxa de transferência de calor pode ser dada por:
Onde é a resistência térmica total do circuito, sendo a soma das seguintes contribuições:
Para o fator de forma, de acordo com o caso 6 da tabela, temos que:
Dessa forma, a resistência térmica bidimensional será:
Logo, a taxa de transferência de calor será:
![]()
Passo 2
As temperaturas das superfícies podem ser definidas por:
![]()
![]()
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Um iglu é construído na forma de um hemisfério, com raio interno de e paredes de neve compacta com uma espessura de .
No interior do iglu, o coeficiente de transferência de calor nas superfícies é de ; no lado de fora sob condições de ventos normais, ele é de . A condutividade térmica da neve compacta é de .
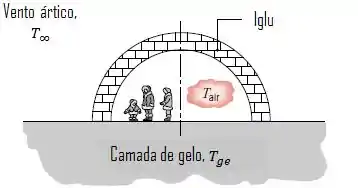
A temperatura da camada de gelo sobre a qual o iglu se encontra é de e a sua condutividade térmica é a mesma da neve compactada.
Considerando que os corpos ocupantes do iglu forneçam uma fonte contínua de calor de no interior do iglu, calcule a temperatura do ar no seu interior quando a temperatura do ar externo é de . Certifique-se de levar em consideração as perdas de calor pelo chão do iglu.
Passo 1
Do calor fornecido do sistema pelos ocupantes, parte flui para o exterior do iglu e parte flui para a camada de gelo. Assim, podemos representar o circuito térmico da seguinte forma:
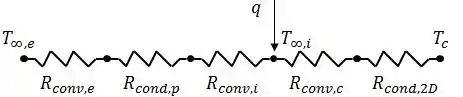
Dessa forma, podemos escrever a taxa de transferência de calor como:
Vamos calcular cada uma das resistências térmicas separadamente, beleza?
Passo 2
Considerando que estamos trabalhando com uma casca semiesférica, teremos:
Convecção externa:
Condução através da parede:
Convecção entre a parede interna do iglu e o ar interno:
Convecção entre o ar interno e o solo:
Condução bidimensional na camada de gelo:
De acordo com o caso 10 da tabela, . Dessa forma, a resistência térmica para esse caso será:
Passo 3
Substituindo todos os valores, teremos:
Agora é só arrumar a casa:
![]()
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptado) Um componente eletrônico na forma de um disco com de diâmetro dissipa quanto montado sobre um grande bloco de uma liga de alumínio (2024), cuja temperatura é mantida a .
A configuração de montagem é tal que há uma resistência de contato de na interface entre o componente eletrônico e o bloco.
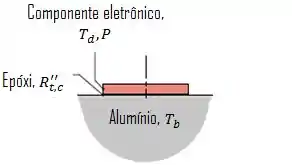
Calcule a temperatura que o componente atingirá, supondo que toda a potência gerada pelo componente deva ser transferida por condução para o bloco.
Passo 1
Como temos a taxa de transferência de calor, a temperatura do componente pode ser calculada utilizando a seguinte expressão:
Vamos calcular as resistências térmicas do circuito.
Passo 2
A resistência de contato será dada por:
Para a resistência bidimensional no disco, vamos usar o caso 10 da tabela, onde o fator de forma vale . Assim:
Passo 3
Finalmente, a temperatura do componente será:
![]()
Resposta
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Água quente é transportada de uma estação de cogeração de potência para usuário comerciais e industriais através de tubos de aço com diâmetro . Cada tubo encontra-se no centro de um bloco de concreto de seção transversal quadrada .
As superfícies externas do concreto estão expostas ao ar ambiente, no qual e .
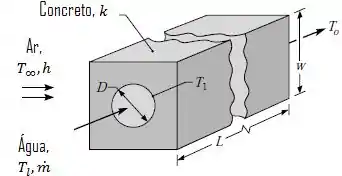
Sendo a temperatura de entrada da água escoando através do tubo igual a , qual é a perda de calor por unidade de comprimento do tubo na proximidade da entrada? A temperatura do tubo pode ser considerada para ser igual à da entrada da água.
Se diferença entre as temperaturas de entrada e de saída da água escoando através de um tubo com de comprimento não puder exceder os , estime a vazão mássica mínima permitida . Um valor de pode ser usado para o calor específico da água.
Passo 1
Sendo a temperatura de entrada da água escoando através do tubo igual a , qual é a perda de calor por unidade de comprimento do tubo na proximidade da entrada? A temperatura do tubo pode ser considerada para ser igual à da entrada da água.
A taxa de transferência de calor pode ser calculada da seguinte forma:
A resistência térmica de convecção vale:
Para a resistência de condução bidimensional, vamos considerar o caso 6 da tabela do fator de forma, onde o mesmo vale . Assim:
Assim, a taxa de transferência de calor será:
Como queremos a taxa de transferência de calor por unidade de comprimento . Dividindo os dois lados da equação por :
![]()
Passo 2
Se diferença entre as temperaturas de entrada e de saída da água escoando através de um tubo com de comprimento não puder exceder os , estime a vazão mássica mínima permitida . Um valor de pode ser usado para o calor específico da água.
Sabendo a diferença entre as temperaturas de entrada e saída, podemos calcular a vazão mássica da seguinte forma:
![]()
Resposta