Correlações para Transferência de Massa
Produzido por Giovanna RonzéTeoria
E aí tudo em cima? Chegou a hora da gente ver algumas correlações para transferência de massa convectiva… Mas afinal pra quê essas correlações? É o seguinte, sabe quando a gente lê um enunciado e ele vem falando que nosso escoamento é em uma placa plana, em uma esfera, em um cilindro ou em um cano? Para cada geometria nós vamos ter uma correlação, sacou?

Essas correlações vão se basear nos nossos, já conhecidos, números adimensionais, beleza? Vamos começar então!
Placa Plana
Se temos uma placa plana e vamos avaliar uma distância em relação ao início da placa, vamos ter um número de Sherwood, para um escoamento laminar, equivalente a:
E podemos encontrar esse valor de Reynolds, com a equação:
Onde é a densidade da mistura de fluidos, o é a viscosidade da mistura de fluidos, o é a velocidade do fluido bulk e o é a distância que estamos avaliando na placa.
Já para avaliar o número de Sherwood no comprimento, , da placa, teremos, para um escoamento laminar, onde :
E para um escoamento turbulento, onde :
Essas mesmas equações podem ser escritas em relação ao fluxo molar, olha só:
Simplificando ainda mais, quando temos um número de Schmidt que esteja entre , temos para um escoamento laminar, onde :
E para um escoamento turbulento, onde :
Agora vamos observar esse escoamento em uma placa plana, no início do escoamento vemos uma camada limite hidrodinâmica antes da camada limite de concentração, olha só:
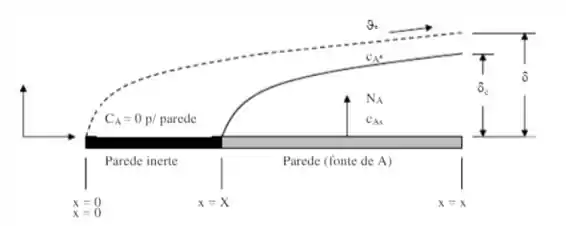
Isso nos dá então as seguintes condições de contorno de concentração:
E com elas, temos um número de Sherwood, dessa forma:
Esfera
No caso de uma esfera, temos um número de Sherwood, de forma geral igual a:
Esse 2 somando aí é a contribuição da difusão molecular e essas duas constantes (C e m), são constantes da própria correlação.
Nesse caso aqui, o número de Reynolds será dado por:
Só trocamos a distância da placa pelo diâmetro da esfera, ok?
No caso da esfera teremos algumas correlações diferentes, olha só! Quando estamos trabalhando com transferência de massa convectiva em uma corrente líquida, vamos ter a correlação de Brian e Hales, onde:
E esse é o número de Peclet, que pode ser dado por: … Mas, essa correlação aí é para quando e se ele for maior que isso???
Aí a gente vai usar a correlação de Levick, que teremos:
Quando estamos em uma transferência de massa convectiva em uma corrente gasosa, vamos ter a correlação de Froessling, onde temos:
Mas atenção, ela só é válida para e , ok?
Mas até agora a gente tava vendo essas correlação em relação a convecção forçada, e se tivermos transferência em convecção natural? Aí a gente usa a relação de Steinberger e Treybal, essa aqui olha só:
E esse a gente pode calcular de duas formas. Se , podemos usar a relação:
E se , usamos a relação:
Mas essa aqui também tem um detalhe importante! Ela só é válida para e , ok?
Beleza, mas quem lembra quem é esse ? Ele é o número de Grashof, é dado por:
Sendo o diâmetro da esfera, o a densidade do fluido nas condições bulk, o a viscosidade do fluido nas condições bulk e o a diferença entre as duas fases que estão em contato.
Cilindro
Quando temos sublimação do cilindro sólido em ar escoando na direção do seu eixo, teremos o seguinte:
Porém essa relação só é válida para e , certo?
Nessa relação é a pressão total do sistema e é a velocidade superficial molar do gás.
Mas e se a gente tiver fora dessa faixa do Reynolds e o Schmidt? Aí podemos usar a correlação de Chilton-Colburn, que nós já vimos, beleza?
Escoamento turbulento através de canos
Nesse caso temos duas correlações. Para e , podemos usar a correlação de Gilliland e Sherwood, que nos dá:
Onde esse é o diâmetro interno do cano, é a composição logarítmica do gás de arraste, avaliado entre a composição da superfície e a corrente bulk, é a pressão total e é o coeficiente de difusividade mássica.
E para a condição em que e , podemos usar a correlação de Gilliland, Sherwood e Linton, que nos diz que:
Transferência de massa em parede molhada
Quando estamos trabalhando com uma parede molhada o coeficiente de transferência convectivo para uma corrente gasosa será a mesma correlação de Gilliland e Sherwood:
Com a mesma restrição que e .
Já se a gente tiver trabalhando com um filme líquido, vamos usar a correlação de Vivian e Peaceman:
Onde temos que é o comprimento de contato… Além disso, esse valor de Reynolds nós vamos calcular da seguinte forma:
Onde temos que é a vazão mássica do líquido, é o diâmetro da coluna e é a vazão mássica do líquido por unidade de perímetro molhado.
Agora vamos fazer exercícios e fixar essa teoria na cabeça!
Esfera
Cilindro
Escoamento turbulento através de canos
Transferência de massa em parede molhada
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Explique a importância das correlações na transferência de massa convectiva.
Passo 1
Fala aí!! Vamos falar sobre a importância das correlações que aprendemos nessa teoria? Vamos lá!
Bom, pensa comigo… imagina que temos apenas fórmulas gerais para tratar diferentes casos de escoamento, ou seja, uma única fórmula para encontrar cada fator adimensional e o coeficiente de massa convectivo… Teoricamente a gente pode até pensar “Melhor dos mundos!”, né?
Mas isso não é verdade, porque depois quando a gente fosse projetar um equipamento iria dar tudo errado! Afinal, teríamos parâmetros que não são condizentes com a realidade!
Então precisamos ter equações que se adequem para cada tipo de forma de escoamento, seja ele em uma placa plana, em uma tubulação, passando por uma esfera e outros… Essas correlações são ajustes do nosso modelo de forma a deixar nossos resultados teóricos o mais próximo possível do experimental, ok?
Show de bola!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria.
Identifique a principal diferença entre as correlações para uma placa-plana e um esfera.
Passo 1
Nessa questão aqui a gente fica tentado a dizer: “Uma é plana e a outra é uma esfera” haha
Mas não é isso que o enunciado quer da gente… Ele quer que a gente olhe para as correlações e verifique sua principal diferença.
Vamos olhar primeiro para a correlação que define o número de Sherwood para um escoamento em uma placa plana, temos para um escoamento laminar:
E para um escoamento turbulento, onde :
Ok! Isso quer dizer que para encontrar o número de Sherwood precisamos do número de Reynolds e do número de Schmidt, certo?
Agora olhando para a correlação de Brian e Hales, no caso de uma esfera, temos que o número de Sherwood, será dado por:
Olha aí! Acabamos de encontrar a principal diferença! Comparando o modelo de placa plana com a correlação de Brian e Hales, para uma esfera, vemos que, no caso da esfera, usaremos um outro número adimensional, o número de Peclet!
Prontinho!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração própria.
Determine o coeficiente de transferência de massa convectiva em um escoamento em uma tubulação de 30 cm de diâmetro interno e 10 km de comprimento.
Dados:
Passo 1
Aee! Vamos fazer continhas!! haha
Nosso enunciado tá pedindo o de um escoamento que acontece em uma tubulação… Hum… Uma tubulação é um cano, certo? Então vamos trabalhar com as correlações de um escoamento turbulento através de um cano, beleza?
O número de Reynolds dado confirma que podemos usar esse modelo, já que estamos em regime turbulento, então partiu!
Temos duas correlações possível pra gente usar, para identificar qual delas é a mais correta, vamos verificar os valores de Schmidt e de Reynolds fornecidos:
Bom, eles se encaixam na condição e , ou seja, vamos usar a correlação de Gilliland, Sherwood e Linton! Ela nos fornece o seguinte:
Como o enunciado está pedindo o coeficiente de transferência de massa convectiva, vamos arrumar essa equação:
Show de bola! Já que temos todos os dados, vamos substituir e encontrar nosso coeficiente!
Prontinho!
Resposta
Exercício Resolvido #4
IFBA - Lista de exercícios de transferência de massa.
A correlação , desenvolvida para calcular o coeficiente de transferência de calor por convecção, , entre uma partícula esférica e um fluido em escoamento, pode também ser utilizada, por analogia, para o cálculo do coeficiente de transferência de massa, . Sabe-se que o Número de Sherwood, , é equivalente ao Número de Nusselt, ; o Número de Schmidt, , é equivalente ao Número de Prandtl, ; é o Número de Reynolds. Considerando o exposto, analise cada uma das afirmações a seguir, julgando-as como verdadeiras ou falsas e justificando sua resposta:
I - Para valores muito baixos de , pode ser obtido por , onde é o coeficiente de difusão molecular de A em uma mistura de A e B, e é o diâmetro da partícula esférica.
II - Para valores muito altos de , pode ser obtido por , onde é o coeficiente de difusão molecular de A em uma mistura de A e B, é o diâmetro da partícula esférica, é a viscosidade cinemática do fluido em escoamento e a velocidade no seio do fluido.
III - , que representa a razão entre as difusividades inercial (momentum) e molecular (de massa), pode ter unidades de .
IV – As melhores estimativas teóricas para provêm da teoria da camada limite.
V – A analogia de Chilton-Colburn pode ser encarada com uma extensão da analogia de Reynolds para , sendo considerada a mais adequada para a previsão de em fenômenos descritos pela teoria da camada limite.
Passo 1
Fala aí!! Partiu encarar esse desafio juntos! Precisamos verificar cada uma dessas opções e dizer se elas são verdadeiras ou falsas, ok?
Vamos começar com a primeira, ela diz que se tivermos valores muito baixos de Reynolds, então o pode calculado por essa fórmula aqui: … Bom, pra começo de conversa vamos reescrever a equação de transferência de calor dada no enunciado, na forma de equação de transferência de massa, baseado nas informações que o problema nos deu, ok?
Vamos lembrar lá da nossa teoria, que essa equação só pode ser aplicada se essas condições forem respeitadas: e , belezinha?
Bom, mas essa opção tá falando do coeficiente convectivo… relembrando que podemos usar a relação, para placa plana, onde:
Arrumando e substituindo o comprimento da placa pelo diâmetro da partícula esférica, vamos ficar com:
Então essa opção está dizendo que para valores de Reynolds muito baixos, vamos ter que:
E sendo assim, acabamos de verificar que essa opção está correta!
Passo 2
Agora vamos para a segunda opção! Ela diz que para valores muito altos de , pode ser obtido por , vamos verificar, sendo:
E substituindo a equação de Sherwood , vamos ter:
Substituindo o número de Reynolds, como sendo:
Vamos ter:
E substituindo também o número de Schmidt:
Ficamos com:
Arrumando essa bagunça toda, ficamos com:
Então nossa segunda alternativa também está correta!
Passo 3
Essa terceira está mais para uma pegadinha, né? Olha só, ela tá dizendo que o número de Schmidt, , pode ter unidades de … Maaaasss a gente sabe que o número de Schmidt é adimensional! Logo ele não tem unidades! E essa opção é falsa!
Passo 4
Agora a nossa quarta opção. Ela diz que as melhores estimativas teóricas para provêm da teoria da camada limite… E essa é uma afirmação que vemos na prática que é verdade! Pois a teoria da camada limite, respeitando as formas de cada escoamento, é uma ótima maneira de encontrar o se a gente não tiver trabalhando com dados experimentais!
Passo 5
Pra fechar, vamos para a última opção! Ela nos afirma que a analogia de Chilton-Colburn pode ser uma extensão da analogia de Reynolds para , sendo considerada a mais adequada para a previsão de em fenômenos descritos pela teoria da camada limite.
Bom, a primeira parte dela a gente sabe de cara que está correta, porque aprendemos isso em teorias anteriores, né? Beleza! Sabemos que sim a analogia de Chilton-Colburn é uma extensão da analogia de Reynolds, mas considerando . Mas agora ela diz que ela representa melhor a teoria da camada limite… hummm… Vamos observar essa imagem aqui:
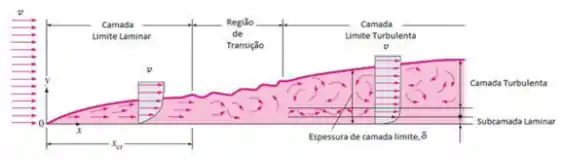
Ela mostra representa a teoria da camada limite e mostra pra gente que temos uma camada laminar, uma região de transição e uma camada turbulenta, bom a analogia de Reynolds não considera, justamente, essa região de transição, enquanto que a analogia de Chilton-Colburn considera. Então, essa afirmação é verdadeira sim!
Resposta
- Verdadeiro
- Verdadeiro
- Falso
- Verdadeiro
- Verdadeiro
Exercício Resolvido #5
Adaptado de Apostila de transferência de massa - Samuel Luporini
Uma coluna de parede molhada de 2 cm de diâmetro, está sendo utilizada para absorver um fluido a partir de uma solução aquosa por uma corrente de ar escoando a 2,5 ft/s. Determinar o coeficiente de transferência de massa na fase gasosa. A coluna é operada a 10 atm e 25°C.
Dados: ; ; ; .
Passo 1
Chegou aquela hora que a gente ama! Fazer mais exercícios!!! haha
Vamos lá! Nosso enunciado está pedindo pra gente determinar o coeficiente de massa na fase gasosa, e deu pra gente um problema onde trabalhamos com uma parede molhada.... Esse é um típico escoamento através de canos!
Como o coeficiente que ele está pedindo é na fase gasosa, a correlação que podemos utilizar é a de Gilliland e Sherwood, dá só uma olhadinha:
Para tudo! Antes de começar as contas precisamos verificar se realmente podemos usar essa correlação… Para isso vamos verificar a seguinte condição dela:
e
Passo 2
Calculando primeiro o número de Reynolds, temos que:
Bom, nós temos todos esses termos, certo? Então vamos a continha!
Opa! Nosso Reynolds está dentro da faixa! Agora falta verificar o número de Schmidt, vamos nessa!
Temos todos os termos, então vamos substituir!
Show! Chegou perto do limite, mas ainda está dentro da faixa de utilização, partiu continhas!!
Passo 3
Vamos então, substituir nossos dados na equação do passo 1, e encontrar o coeficiente convectivo!
Prontinho!
Resposta
Exercício Resolvido #6
Elaboração própria.
Um fluido está escoando em um cilindro de 5 cm de diâmetro na direção do seu eixo, com uma velocidade de 1,5 m/s. O cilindro se encontra a 5 atm e 30°C. Sendo o coeficiente de difusão do fluido na água dado por 0,0016 mm²/s. Determine a velocidade superficial molar desse sistema.
Dados: ; ; ; .
Passo 1
Olha só, o enunciado está dizendo que temos um escoamento em um cilindro… opa! Podemos usar a correlação para esse caso, olha ela aí:
E ele tá pedindo pra gente determinar a velocidade superficial molar do sistema… hummm… lembra dela? É esse que aparece na correlação!
Mas antes de começar as contas precisamos verificar se realmente podemos usar essa correlação… Para isso vamos verificar a condição dela:
e
Passo 2
Calculando o número de Reynolds, temos:
Substituindo nossos dados, ficamos com:
Show! Nosso Reynolds está dentro da condição! Agora vamos verificar o número de Schmidt:
Temos todos os termos, então vamos substituir!
Beleza!
Passo 3
Vamos encontrar a velocidade superficial molar do sistema:
Isolando o , temos:
Substituindo nossos dados ficamos com:
Tranquilo?
Resposta
Exercício Resolvido #7
Adaptado de Apostila de transferência de massa - Samuel Luporini
Uma placa de silício de 10 cm é posicionada a 4 cm a partir de uma placa quente. A temperatura do processo é 800 K e a pressão do sistema é 101,3 KPa. Considerando o caso limitante onde o escoamento do gás rico em está a uma velocidade média de 100 cm/s. Determinar o coeficiente de transferência de massa global, no centro da placa.
Dados: ; ; .
Passo 1
Fala aí! Vamos de exercício! O enunciado já tá dizendo que estamos trabalhando com uma placa plana… Aí a gente lendo o problemas, meio que se prepara para usar essa correlação de placa plana aqui:
Ops! Mas o que ele está pedindo não aparece nessa correlação! Mas calma! Olha com calma! Essa correlação entrega pra gente o número de Sherwood, né?
E com esse número representa? Humm… Ele tem uma equação básica que diz que:
Olha aí!! O coeficiente de transferência de massa global apareceu! Então é só a gente seguir essa ideia, acha o Sherwood e depois acha o coeficiente!
Passo 2
Nessa equação, precisamos do número de Reynolds, então vamos encontrá-lo:
Substituindo nossos dados, ficamos com:
Show! Agora precisamos do número de Schmidt:
Temos todos os termos, então vamos substituir!
Beleza!
Passo 3
Agora vamos encontrar o número de Sherwood!
Agora partiu encontrar o coeficiente que o enunciado pediu! Isolando quem a gente quer na equação, ficamos com:
Substituindo os valores:
Prontinho!
Resposta
Exercício Resolvido #8
Adaptado de Apostila de transferência de massa - Samuel Luporini
Estimar a distância de percurso de uma gota esférica de água em escoamento, com 1,0 mm em diâmetro, em ar seco imóvel a 323 K. Considerando um balanço de força na partícula esférica no meio do fluido, podemos mostrar que a velocidade terminal é:
Dados: ; ; ; .
Passo 1
Vamos de exercício! Estamos trabalhando com uma gota esférica, o enunciado deu pra gente uma maneira de calcular a velocidade terminal e nos pediu a distância de percurso… Vamos pensar, baseado nas nossas informações, qual equação que relaciona velocidade terminal com a distância?
Bingo! O número de Reynolds! Dá só uma olhada nele aqui:
Show! Então já sabemos o que fazer… Partiu!!
Passo 2
Começamos calculando a velocidade terminal, usando a equação dada, ok?
Bom, temos o diâmetro da partícula, as densidades e sabemos a gravidade… Mas quem é esse ? Esse cara aí é o coeficiente de arraste, ele é uma função de Reynolds e da esfericidade, mas sempre que a gente trabalhar com uma partícula esférica podemos considerar ele como 1!
Então vamos as contas:
Passo 3
Agora partiu encontrar a distância usando o número de Reynolds!
Isolando , temos:
Não esqueça que aqui estamos trabalhando com o escoamento da água no ar seco, isso quer dizer que as propriedades que vamos colocar na equação são as da água, beleza?
Encontramos o comprimento do escoamento!