Difusão sem Reação Química
Produzido por Giovanna RonzéTeoria
Aqui a gente vai ver como que a gente pode modelar alguns sistemas onde tá acontecendo transporte de massa. Isso vai servir pra gente encontrar:
- O fluxo ou a taxa de transferência de massa;
- A concentração em um determinado ponto do sistema;
- Em qual ponto do sistema se tem uma concentração específica;
- A difusividade de uma espécie naquele sistema.
Nesse tópico aqui, a gente vai ver especificamente pra quando não tiver acontecendo reação no meio, beleza? Então bora lá ver que tipo de situação a gente pode encontrar!
Difusão Binária Unidimensional em Gás Estagnado

Calma, vou explicar agorinha o que que é isso. Quando falamos de difusão binária, significa que só tem 2 substâncias envolvidas.
Unidimensional é porque a difusão está acontecendo em uma direção só, não tem gradiente de concentração nas outras direções.
E, gás estagnado significa que uma das substâncias (o gás) não está se misturando na outra. Ficou mais claro? Vamos ver como que esse experimento é feito na prática, ele é chamado de célula de Arnold.
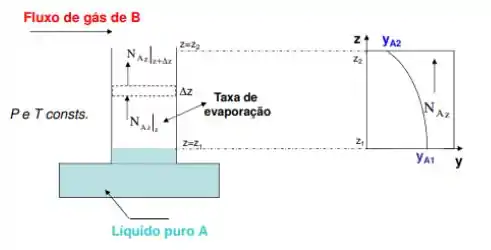
A célula de Arnold então nada mais é do que um processo de evaporação do líquido A em B, onde B é um gás estagnado, ou seja, que não se mistura e nem reage com A. Nesse caso então só existe fluxo de transferência de massa de A para B. O fluxo de transferência de massa de B pra A é !
Outra característica desse tipo de sistema também é que a altura do líquido no tubo não varia. É como se tivesse uma alimentação contínua de A.
Beleza, agora que a gente sabe a condições, vamos entender como que a gente usa o que a gente tem!
Primeiro, se a gente fizer um balanço de massa num espacinho bem pequenininho dentro da extensão do nosso tubo (que nem ali na figura), a gente vai ver que tudo que tá entrando de A nesse voluminho de controle é igual a tudo que está saindo.
Isso quer dizer que o fluxo de massa de A no sistema é constante ao longo do eixo z!
Beleza, mas como eu acho o fluxo?
Em um sistema binário, o fluxo em z é dado pela expressão:
Como a gente viu que o fluxo de z é nulo, a gente pode reescrever essa relação assim:
Passando esse dz pro outro lado e integrando chegamos numa expressão real pro fluxo!
E se a gente quiser construir um perfil de concentração?
A gente precisaria avaliar de pedacinho em pedacinho dentro do tubo, e a gente consegue resolver isso matematicamente já que sabemos que a derivada do fluxo é igual 0 e a gente tem a expressão do fluxo.
Juntando as duas equações temos que:
Tirandos as constantes e resolvendo as duas derivações chegamos na seguinte expressão:
Usando uma condição de contorno genérica:
Finalmente temos que:
Como estamos falando de um sistema binário:
Para cálculos de engenharia, as vezes é mais interessante saber uma concentração média ao invés do perfil de concentração completo.
Que nem lá em transcal, define-se então uma média logarítmica de concentração:
Em termos de B:
Em termos de A:
Essa média também pode ser expressa em termos da pressão parcial quando tiver falando de gás!
Substituindo em :
Contradifusão Equimolar
Nesse caso aqui, diferente dos outros, o gás vai se misturar no líquido e o líquido vai evaporar pro gás, por isso contradifusão.
Equimolar vem do fato de que esses fluxos tem que ter a mesma quantidade. Então o mesmo número de mols que sai do líquido pro gás, é o número de mols que vai do gás pro líquido. Beleza?
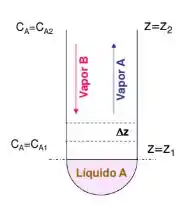
Outra situação que pode acontecer são dois reservatórios interligados, cada um com uma mistura de A e B numa proporção diferente.
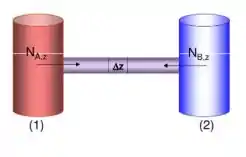
Assim que se abrir uma conexão entre os dois, pra cada mol de A que vai de 1 pra 2, vai também um mol de B de 2 pra 1. Isso até eles atingirem uma concentração igual de equilíbrio!
Então, a contradifusão equimolar vai acontecer em diversos tipos de situação e a gente vai ter que saber identificar caso o problema não diga direto pra gente, beleza?
Em todos os casos que falamos aí em cima, reina a relação:
Relembrando a equação pro fluxo em um sistema binário:
Agora sabemos que o segundo termo vai ser igual a zero, então:
Integrando dos dois lados vamos chegar em uma expressão pro fluxo!
Usando as condições de contorno:
Finalmente:
E também pode ser em função da pressão parcial quando falarmos de gases!
Nesse caso aqui, também vale que a derivada do fluxo é igual a 0, ou seja, o fluxo é uma constante!
Pra determinar o perfil de concentração juntando uma equação na outra:
Se for constante (o que geralmente é considerado):
Usando as seguintes condições de contorno:
Finalmente a expressão pro perfil de concentração:
Conceito de Filme
O conceito de filme lembra o conceito de camada limite. É como se numa camada bem fininha de espessura em cima do líquido, houvesse uma resistência à difusão pela mudança de fase.
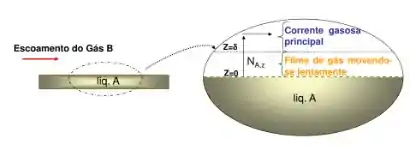
Esse conceito é usado para calcular o lá da convecção. (Relembrando )
O é o coeficiente convectivo, que é como se fosse o , mas pra quando estamos falando de convecção e não difusão. A convecção é quando temos transporte de massa pela movimentação de um fluido, na difusão a gente considera o fluido paradinho.
Basicamente a relação que encontraram é essa aqui:
E se quisermos pôr em função da pressão parcial do gás:
Show de bola, agora a gente tá munido de váaarias equações pra calcular o que a gente precisa em cada caso. Bora então exercitar!
Contradifusão Equimolar
Conceito de Filme
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Quais são as hipóteses que podemos assumir quando estamos em um processo em que a transferência de massa ocorra sem reação química, em regime permanente e com fluxo unidirecional?
Passo 1
Fala aí! Essa questão é pra saber se estamos ligados na teoria!
Quando estamos resolvendo uma questão que apresenta regime permanente, podemos assumir algumas hipóteses que auxiliam na nossa resolução, olha só:
Se estamos trabalhando com regime permanente, isso significa que:
Se não está ocorrendo reação química, isso quer dizer que:
E se o fluxo é em uma dimensão apenas, assumimos que:
∇constante
Isso faz com que a equação de fluxo, que inicialmente seria assim:
Fique com essa cara aqui:
Facilitando nossos cálculos! Show de bolinhas!
Resposta
Passo 1.
Exercício Resolvido #2
Transferência de calor e massa - Incropera
Considere a interface entre o ar atmosférico e um corpo de água, ambos a 17°C.
- Quais são as frações molar e mássica da água no lado do ar da interface? E no lado da água da interface?
- Quais são as frações molar e mássica do oxigênio no lado do ar da interface? E no lado da água da interface? O ar atmosférico pode ser considerado contendo 20,5% de oxigênio em volume.
Dados: e
Passo 1
E aí? Tudo em cima? Vamos fazer uns exercícios para fixar o conteúdo, beleza?
Esse enunciado tá dizendo pra gente que o ar e um corpo de água estão na mesma temperatura… A letra a pediu as frações molares e mássicas da água nas duas interfaces!
Pra fazer isso, vamos considerar que o ar e o vapor d’água se comportam como gás ideal, que temos equilíbrio termodinâmico na interface e o peso molecular do ar é independente da concentração… Agora sim!!
Com nossas hipóteses podemos dizer que:
Então:
E lembrando que e , temos:
E sendo:
Opa! A gente vai ter então:
Temos então que .
Passo 2
E lembrando que a fração molar é equivalente a fração volumétrica, temos:
Então vamos calcular:
Agora vamos achar a fração molar do :
Portanto a fração mássica de na água, será:
Prontinho!
Resposta
- , e .
- e .
Exercício Resolvido #3
Engenharia química Santos - SP - Lei de Fick
Em um tubo de de comprimento há difusão de amônia gasosa (A) em nitrogênio () gasoso (B) a de pressão a (). No ponto 1 a pressão é de e no ponto 2 a pressão é de , e a difusividade é .
Dado:
- Calcule o fluxo específico em estado estacionário;
- Calcule o fluxo específico em estado estacionário.
Passo 1
Vamos começar pelo começo… Partiu letra a! Precisamos do fluxo , antes de tudo vamos anotar nossos dados:
Agora usando a equação do fluxo, vamos ter:
Substituindo os valores, temos:
Passo 2
Agora é a vez da letra b! Precisamos encontrar o … Vai ser quase igual a letra a, mas agora não temos o e o , vamos achar eles antes!
Agora vamos fazer o mesmo para o :
Beleza! Agora é só usar a equação do fluxo e teremos:
Substituindo os valores, temos:
O fluxo negativo significa que ele está indo do ponto 2 para o ponto 1, ou seja, o sentido contrário ao que imaginamos!
Prontinho!
Resposta
Exercício Resolvido #4
USP - Fenômenos de transporte III - Aula 06
A pressão em uma tubulação que transporta gás hélio a uma taxa de é mantida a pela ventilação de hélio para a atmosfera através de um tubo de de diâmetro interno, que se estende no ar, como mostrado na Figura. Supondo que ambos, o hélio e o ar atmosférico, estão a , determinar:
- a vazão mássica de hélio perdido para a atmosfera através do tubo;
- a vazão e a fração mássica de ar que se infiltra na tubulação;
- a velocidade do escoamento no fundo do tubo onde este está ligado à tubulação que vai ser medida por um anemômetro em regime permanente.
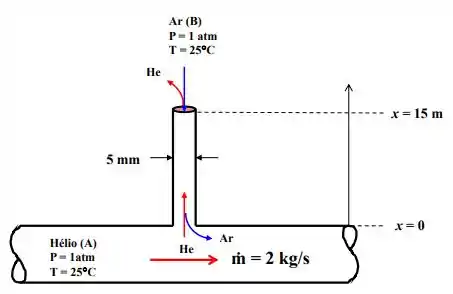
Dados: O coeficiente de difusão do hélio no ar .
A Massa molar do ar e a do hélio
A constante dos gases
Passo 1
Fala aí! Vamos começar fazendo algumas suposições que nos ajudem a resolver nosso exercício, beleza?
A primeira é que estamos trabalhando com regime permanente, o ar e o hélio nós vamos considerar como sendo gases ideias, não ocorrem reações químicas no tubo e que a concentração de ar na tubulação e de hélio na atmosfera são desprezíveis… Feito isso, agora partiu ir pra resolução!
Temos um problema com dois grandes reservatórios de misturas de gases ideais ligados entre si por um canal e as concentrações das espécies em cada reservatório permanecem constantes… Ou seja, estamos trabalhando com contradifusão equimolar!
Vamos começar resolvendo a letra a! Ela quer a vazão mássica de hélio que vai para a atmosfera… Pra começar, vamos encontrar a área do nosso escoamento:
Com o diâmetro dado, vamos ter:
Nossas condições de contorno dizem que no fundo do tubo a pressão parcial de hélio é , isso quer dizer que:
E sabendo que no topo, em , a vazão molar é:
Substituindo os dados que temos:
Então a vazão mássica será:
Substituindo nossos valores:
Show! Partiu letra b!
Passo 2
Agora precisamos da fração mássica do ar que entra na tubulação, vamos nessa!!
Lembrando que em um processo de contradifusão equimolar temos que , então:
Opa! Então vamos achar a vazão mássica dentro da tubulação:
Então podemos encontrar a fração mássica de ar na tubulação, será:
Lembrando que a massa total será A vazão mássica total menos a vazão mássica em A e em B, vamos ter:
Opa! Isso significa que o ar no interior da tubulação é desprezível, ou seja, nossa suposição inicial se confirmou!
Passo 3
Agora só falta a letra c! Precisamos encontrar a velocidade média do escoamento no fundo do tubo… Para isso, vamos começar encontrando a vazão mássica líquida através do capilar:
Como a gente está considerando o hélio e o ar como gases ideais, podemos encontrar a densidade do hélio assim:
Beleza! Com esses dados podemos encontrar a velocidade com a relação:
Show de bola! Terminamos!
Resposta
Exercício Resolvido #5
Fundamentos de transferência de massa - Marco Aurélio Cremasco
Obtenha a distribuição da fração molar do dióxido de carbono que difunde em uma película estagnada de ar seco de de profundidade a e . Essa película está num capilar, o qual contém ácido sulfúrico. O é absorvido instantaneamente ao atingir o líquido. A concentração do na boca do capilar é em mols.
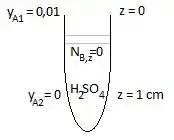
Passo 1
Vamos começar fazendo algumas suposições para facilitar a resolução do exercício, beleza?
A primeira é que estamos trabalhando com regime permanente, , além disso não ocorrem reações químicas, , e também estamos trabalhando com fluxo em uma dimensão apenas, ∇constante.
Agora partiu encontrar a distribuição da fração molar do ! Usando a equação do fluxo global em A, temos:
E sendo constantes, temos:
Se a pressão e a temperatura são constantes, então o coeficiente de difusão, também é! Logo:
Integrando duas vezes, vamos ter o seguinte:
Isolando o , vamos ter:
Passo 2
Agora vamos dar uma olhada nas nossas condições de contorno:
Em
, isso acontece porque A absorvido instantaneamente.
Usando nossas condições de contorno, nossa distribuição de fração molar do dióxido de carbono será dada por:
Conseguimos!!
Resposta
Exercício Resolvido #6
Transferência de calor e massa - Incropera
Hidrogênio a uma pressão de 2 atm escoa no interior de um tubo com 40 mm de diâmetro e espessura de parede de 0,5 mm. A superfície externa está exposta a uma corrente de gás na qual a pressão parcial do hidrogênio é de 0,1 atm. A difusividade mássica e a solubilidade do hidrogênio no material do tubo são e , respectivamente. Quando o sistema encontra-se a 500 K, qual é a taxa de transferência de hidrogênio através da parede do tubo por unidade de comprimento (kg/(s · m))?
Passo 1
Fala aí belezinha? Essa questão tá pedindo pra gente a taxa de transferência de hidrogênio através da parede do tubo… Vamos achar então! Mas antes de tudo, precisamos fazer algumas suposições:
A primeira é que estamos com difusão constante na direção radial, temos uma concentração molar total uniforme na parede, não temos reação química e estamos em um meio estacionário, show de bola? Agora vamos começar a calcular:
Para achar a transferência de massa por unidade de comprimento podemos usar a equação:
Precisamos encontrar o e o , lembrando que:
Vamos ter que:
E para o segundo:
Opa! Show de bola! Agora vamos substituir tudo na nossa equação:
Beleza pura!
Resposta
Exercício Resolvido #7
Adaptado de Fundamentos de transferência de massa - Marco Aurélio Cremasco
Dióxido de carbono difunde em uma película estagnada de ar seco de de profundidade a e . Essa película está num capilar, o qual contém ácido sulfúrico. O é absorvido instantaneamente ao atingir o líquido. A concentração do na boca do capilar é em mols. Calcule a concentração média e o fluxo global molar do absorvido na interface gás/líquido.
Dado:
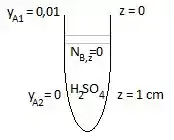
Passo 1
Fala aí! Pra começar nossa brincadeira aqui, vamos dizer que:
e
Para calcular a concentração média, vamos começar encontrando o , beleza?
E podemos encontrar o com a equação:
E sendo:
Teremos então:
Agora temos o nosso :
Beleza! Agora vamos encontrar a concentração total da mistura, considerando que o gás é ideal, vamos ter:
Sendo , , e usando , vamos ter:
Show! Temos a concentração e a fração média, então podemos encontrar a concentração média:
Prontinho! Primeira parte ok!
Passo 2
Agora precisamos encontrar o fluxo global molar do , para isso podemos usar a equação:
Opa! Temos todos os temos! Então vamos substituir na equação:
O fluxo global será:
Show de bolinhas! Tudo ok!
Resposta
Exercício Resolvido #8
Adaptado de USP - Fenômenos de transporte III - Aula 05
Um gás “A” difunde por uma película estagnada de ar (gás “B”), de de profundidade num tubo capilar que contém um determinado ácido. Na interface gás/líquido o gás “A” é absorvido instantaneamente pelo ácido. A concentração do gás na borda do recipiente é em moles e na superfície gás/líquido é nula. Considerando que o processo de transferência de massa ocorra em regime permanente e temperatura e pressão constante, determine o perfil de fração molar do soluto “A” entre a borda do tubo e a superfície gás/líquido.
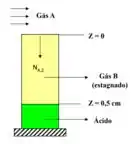
Passo 1
Assumindo as hipóteses:
- Estamos trabalhando com regime permanente, ;
- Não ocorrem reações químicas, ;
- O fluxo é em uma dimensão apenas, ∇constante.
Agora partiu encontrar o perfil da fração molar! Usando a equação do fluxo global em A, temos:
E sendo constante, temos:
Se a pressão e a temperatura são constantes, então o coeficiente de difusão, também é! Logo:
Integrando, vamos ter o seguinte:
E integrando novamente, temos:
Ficamos então com:
Passo 2
Agora vamos verificar nossas condições de contorno:
Para
Para
Usando as condições de contorno, vamos ter que:
Ficamos com:
Reorganizando nossa equação, ficamos com:
Prontinho!