Difusão com Reação Química
Produzido por Giovanna RonzéTeoria
Nesse tópico aqui, a gente vai aprender a modelar alguns sistemas onde tá acontecendo transporte de massa e as moléculas estão reagindo quimicamente. Ou seja, ou elas estão aparecendo ou desaparecendo ao longo do processo. Essas reações podem ser basicamente de 3 tipos:
Reação Heterogênea – É uma reação que acontece numa superfície apenas. Pode ser a reação entre um líquido e um sólido, em que a reação só acontece na superfície desse sólido, que é onde tem o contato entre as duas substâncias.
Reação Homogênea – É aquela reação que acontece no meio líquido de forma uniforme. Então pensa num copo cheio, que tá acontecendo uma reação lá dentro dele todo.
Reação Pseudo-Homogênea – É uma reação que acontece dentro dos poros de um catalisador, por exemplo. Onde a reação acontece, mas a substância ainda tem que se difundir pra fora desse poro.
A gente viu que o balanço diferencial pra uma espécie é descrito por essa equação aqui:
Vamos ver então como esse termo de reação fica em cada caso!
Difusão com Reação Química Heterogênea
Então, ali em cima eu falei que o termo é referente a reação no processo, mas esse termo é usado apenas pra reações homogêneas.

Pra reações heterogêneas, como ela acontece em uma superfície (em geral no limite do volume de controle), ela entra na verdade como uma das condições de contorno do problema.
Mas vamos lá!
Em vários sistemas industriais acontece de um reagente se difundir até entrar em contato com a superfície de um sólido e então reagir. A velocidade desse processo pode ser controlada pela:
- Difusão: Quando difusão é lenta e a reação é rápida. Então basicamente a velocidade pra tudo acontecer é a velocidade da difusão.
- Reação: Quando a reação é lenta e a difusão é rápida quando em comparação. Nesse caso a reação limita a transferência de massa.
Vamos pegar então um exemplo! Esse aqui é de partículas esféricas de carvão (Carbono puro) são queimadas para gerar energia:
Pela reação da combustão incompleta em estado estacionário, temos que pra cada mol de gás oxigênio chegando na superfície do carvão, teremos 2 moles de monóxido de carbono saindo.(Se não fosse estado estacionário, a quantidade de moles que chega e que sai estaria mudando ao longo do tempo)
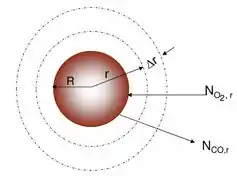
![]() Vamos avaliar primeiro o fluxo e a taxa de transferência de massa. Para isso, o balanço!
Vamos avaliar primeiro o fluxo e a taxa de transferência de massa. Para isso, o balanço!
![]()
0 (E.E.) 0 (Sem reação homogênea)
Com as simplificações e usando coordenadas esféricas temos que:
Porém, como o fluxo é radial, podemos simplificar mais uma vez e temos:
Disso, podemos concluir que:
Como o raio não é constante, porque a esfera vai diminuindo conforme o carbono é consumido, logo o fluxo não é constante!
Mas o fluxo de que? Então, esse balanço ai vai valer tanto pro quanto pro . Pra esfera de carbono a gente diz que o fluxo de difusão é igual a zero, porque ela é sólida e vai ficar paradinha lá, então não tá acontecendo transporte de carbono puro. Beleza?
Vamos então considerar que A é então o nosso gás oxigênio. Como é que fica então a expressão pro fluxo?
A gente já viu que a expressão pro fluxo é escrita como:
Nesse caso então ela vai ficar assim:
Pela estequiometria da reação, a gente pode concluir que:
Repara que o sinal negativo aparece, porque os fluxos de massa acontecem em direções opostas!
Ai agora a gente consegue substituir e ter a expressão pro fluxo assim:
Dando uma mexidinha nos temos ela fica com essa cara:
Para nossas condições de contorno temos que:
Multiplicando o lado esquerdo por conseguimos integrar e obter finalmente o fluxo:
Com o fluxo podemos então calcular a taxa de transferência de massa ():
Agora vamos avaliar a variação do raio da esfera de carbono em função do tempo!
Pra isso vamos precisar fazer um balanço integral na esfera em relação ao Carbono , pois assim avaliamos o volume como um todo!
Esse balanço tá dizendo pra gente que a variação da massa do Carbono na esfera (termo do lado esquerdo) é igual à tudo que saiu de massa de Carbono à partir da superfície, já que a reação é na superfície.
Esse fluxo de massa de carbono que a gente colocou no lado direito vem da estequiometria, já que já sabemos o fluxo pro !
Como o volume da esfera é descrito por , onde é uma função do tempo, temos que:
Passando dt pro outro lado e integrando temos finalmente que:
Onde é o raio inicial da esfera!
Difusão com Reação Química Homogênea
Existem várias situações onde as reações industriais acontecem todas em uma fase só, seja ela líquida ou gasosa.
A absorção, por exemplo, é uma operação de separação em que você dissolve uma das espécies de uma mistura gasosa em um líquido que tem afinidade por essa molécula. Ai dependendo, essas moléculas podem reagir ou não.
Vamos então analisar um exemplo de absorção:
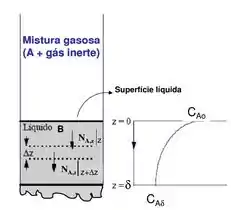
Vamos considerar que:
- Na superfície líquida a concentração de A é
- A altura do líquido é e no fundo , ou seja, não tem componente A no fundo
- Não há movimentação no fluido, ou seja, sem convecção
- Estado estacionário
- Difusão unidimensional, ou seja, variação na concentração apena no eixo vertical
- A cinética da reação é de primeira ordem :
Montando o balanço:
Aplicando agora as simplificações:
Analisando a expressão do fluxo:
Aplicando as simplificações:
Juntando uma com a outra temos que:
Isso ai tem cara de EDO, e a solução geral dela é essa aqui:
A gente vai ter como condições de contorno:
Com isso a gente vai encontrar como constantes:
Finalmente nossa expressão pra concentração em função de z é:
O fluxo mássico que é determinado por:
Vai ficar então, quando z=0:
Repara que quando a reação for muito rápida e :
Ou seja, não importa porque a reação é tão rápida que A não chega até o fundo.
Difusão com Reação Química Pseudo-Homogênea
Um sólido poroso tem uma área superficial interna gigante, e em toda essa área é possível que a reação aconteça.
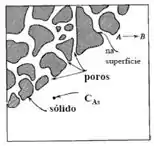
Agora vamo pensar aqui comigo, é muito mais provável que a reação aconteça logo no comecinho do que lá dentro do poro. Então o que rola é que acaba fazendo um gradiente de concentração em direção ao centro da partícula.
Repara que pela imagem já dá pra ter uma ideia de que é difícil pra caramba descrever a difusão dentro dos poros. Então o método que costuma ser usado nesses casos é considerar:
- A geometria esférica da partícula em função do raio R;
- A reação química irreversível homogênea;
- A concentração na superfície igual a concentração no meio do fluido;
- Difusividade efetiva da difusividade em sólidos.
As únicas diferenças então pro que a gente viu no caso anterior é que o coeficiente de difusão vai ser calculado pela difusividade efetiva em sólidos porosos.
E quando a gente for avaliar a taxa de reação, a gente vai multiplicar a constande k pela razão a:
Então pra uma reação de primeira ordem vai ficar assim:
Ufa, acabou! Bora então praticar!
Difusão com Reação Química Homogênea
Difusão com Reação Química Pseudo-Homogênea
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Quais os três tipos de reação que podemos encontrar em processos de difusão? Dê as características de cada uma delas.
Passo 1
Uma questãozinha teórica para aquecer os tamborins, ok? Vamos lá!
Bom, nós podemos encontra processos de difusão com reação homogênea, reação heterogênea e reação pseudo-homogênea.
Vamos agora escrever as características de cada uma, beleza?
A reação heterogênea é aquela que acontece em apenas uma superfície. Pode ser entre um líquido e um sólido, em que a reação só acontece na superfície deste sólido, onde teremos o contato entre as duas substâncias.
Já a reação homogênea, acontece no meio líquido de forma uniforme. Se tivermos um copo cheio de água, esse tipo de reação vai acontecer no interior do copo.
E por último, mas não menos importante, temos a reação pseudo-homogênea, que acontece dentro de poros e ainda vai se difundir para fora dele, é o exemplo de reações que acontecem dentro dos poros de um catalisador.
Belezinha? Tudo ok então!
Resposta
Passo 1.
Exercício Resolvido #2
USP - Fenômenos de Transporte III - Professor Gerônimo
Considere um reator catalítico onde se realiza uma reação irreversível do tipo:
Imagine que a partícula catalítica esteja rodeada por uma película gasosa através do qual difunde o reagente A até alcançar a superfície não-porosa do catalisador. Suponhamos que a reação ocorra instantaneamente sobre a superfície do catalisador e que o produto “B” difunda no sentido contrário do reagente “A”. Considerando o processo de transferência de massa em regime permanente e a T e P constantes e que a reação ocorra sobre uma superfície plana do catalisador, determine o perfil da fração molar e o fluxo molar do soluto “A” em função da espessura da película gasosa “”.
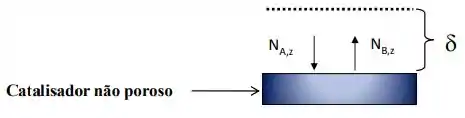
Passo 1
Show de bolinhas! Então nós temos uma superfície catalítica, estilo plana plana, onde ocorre a reação:
Certo? E nosso enunciado pede pra gente o perfil da fração molar e o fluxo molar, sendo a pressão e a temperatura constantes… Humm… Nossa solução então deve obedecer a seguinte equação:
Mas tá enorme isso aí, né? Vamos fazer algumas considerações, beleza?
A primeira é que estamos trabalhando em regime permanente, então: ;
A segunda é que o fluxo de , vai ser apenas na direção , então: ∇;
E a terceira é que não temos reação química homogênea, logo:
Com essas considerações nossa equação, vai ficar com essa cara aqui:
Teremos assim, um fluxo total até a superfície do catalisador, igual a:
E pela estequiometria da nossa reação, temos:
E substituindo isso ali em cima, vamos ter:
Arrumando essa equação, teremos:
Ficamos então com:
E como vimos que , ficamos com:
E como nosso enunciado disse que temos pressão e temperatura constantes, nosso e , também vão ser constantes, logo:
Integrando isso aí, vamos ficar com:
E integrando novamente:
Ficaremos então, com:
Passo 2
Agora vamos aplicar algumas condições de contorno! A primeira é que:
Em:
Opa! Então vamos ter que:
Vamos ter então:
E usando a segunda condição de contorno, devido a reação ser instantânea, temos que:
Em:
Isso quer dizer que:
Substituindo o que já encontramos, ficaremos com:
Agora vamos substituir e na equação que a gente tinha antes, teremos então:
Vamos dividir todos os termos por 2 para simplificar, ok?
E pela “regra do peteleco”:
Show! Vamos ficar então:
Opa! Já encontramos a expressão para o perfil da fração molar! Agora falta o fluxo … Vamos nessa!
Passo 3
Se a gente considerar um fluxo constante sobre a superfície do catalisador, vamos ter:
contante
Integrando a gente vai ficar com:
Nosso fluxo, será então:
Conseguimos!!
Resposta
Perfil da fração molar:
Fluxo de :
Exercício Resolvido #3
USP - Fenômenos de Transporte III - Professor Gerônimo
Um reator catalítico é usado para transformar água () em água pesada (). Supondo que o processo possa ser simplificado para o estudo da transformação de em no reator catalítico, onde na superfície do catalisador em ocorre uma reação instantânea e irreversível do tipo:
Encontre uma expressão para o perfil da fração molar em função da espessura e do fluxo molar do reagente na superfície do catalisador em . Suponha que em a fração molar do reagente ( ) seja igual a e em seja nula. Considere que a reação ocorra sobre uma superfície plana do catalisador e que o processo de transferência de massa ocorra em regime permanente e que o reator esteja operando a T e P constante.
Passo 1
Vamos começar fazendo algumas considerações, beleza?
A primeira é que estamos trabalhando em regime permanente, então: ;
A segunda é que o fluxo de , vai ser apenas na direção , então: ∇;
E a terceira é que não temos reação química homogênea, logo:
Com essas considerações, vamos ter que a equação:
Vai ficar com essa cara aqui:
Teremos assim, um fluxo total até a superfície do catalisador, igual a:
E pela estequiometria da nossa reação, temos:
E substituindo isso ali em cima, vamos ter:
E organizando teremos:
E como vimos que , ficamos com:
Como a gente tem pressão e temperatura constantes, nosso e , também vão ser, então podemos escrever assim:
Integrando isso aí, vamos ficar com:
E novamente:
Ficaremos então, com:
Passo 2
Agora vamos aplicar as condições de contorno do enunciado! A primeira dia que:
Sendo assim:
Vamos ter então:
E usando a segunda condição de contorno, que diz que:
Temos que:
Ficaremos então com:
Agora vamos substituir e na equação que a gente tinha antes, teremos:
Organizando isso tudo aí, vamos ficar com:
Beleza pura! Encontramos a expressão para o perfil da fração molar!
Resposta
Exercício Resolvido #4
USP - Fenômenos de Transporte III - Professor Gerônimo
O soluto-reagente decompõe-se na superfície de uma lâmina catalítica sólida não-porosa segundo a reação irreversível de primeira ordem . O composto faz parte de uma mistura gasosa estagnada de espessura em volta da placa. Estabeleça as equações para o fluxo na superfície da partícula quando:
- A difusão do soluto controla o fluxo de matéria;
- A reação química na superfície da partícula controla o fluxo de matéria.
Passo 1
Fala aí! Partiu resolver essa questão juntinhos? Vamos lá!
Bom, o enunciado dá pra gente algumas informações importantes. Ele diz que estamos trabalhando com uma difusão com reação química heterogênea e ela ocorre na superfície de uma lâmina catalítica não-porosa, certo?
E o que ele pede é a difusão quando o soluto controla o fluxo de matéria, né? E a gente pode usar essa equação aqui:
E se a gente levar em conta as condições de contorno, vamos ter que o fluxo global de , será:
E considerando que estamos trabalhando com , teremos:
E ainda podemos separar esse nosso logaritmo, ficando com a equação assim:
Passo 2
A equação química que foi dada pra gente é:
Então nossos coeficientes estequiométricos são:
Opa! Já podemos encontrar o nosso , ele vai ser:
Substituindo:
Agora voltando na nossa equação, vamos ficar com:
Opa! Então teremos:
Vish! Deu zero para tudo que é lado! Mas não pode, porque temos indeterminações, né? Partiu usar L'Hôpital então pra mudar isso aí, ficaremos com:
Como, na letra a, é a difusão que controla o fluxo, então:
E sendo assim nossa equação vai ficar:
Terminamos a letra a, show de bola?
Passo 3
Agora na letra b, temos o caso em que a equação química da superfície é que controla a difusão, certo?
Opa! Isso quer dizer que , mas se for assim, vamos ter que:
Peraí! Se , isso quer dizer que não temos uma reação química!!!

Calma aí! Nós temos reação química sim! É que a gente não pode esquecer que nesse caso o efeito do fenômeno difusivo vai ser desprezível, então, levando em conta a continuidade de matéria, vamos ter que na verdade a difusão será dada pela resistência, assim:
E isso quer dizer que:
Arrasamos! Conseguimos terminar as duas letras!
Resposta
Exercício Resolvido #5
Adaptado de USP - Fenômenos de Transporte III - Professor Gerônimo
Considere um reator catalítico onde se realiza uma reação irreversível do tipo:
Imagine que a partícula catalítica esteja rodeada por uma película gasosa através do qual difunde o reagente A até alcançar a superfície não-porosa do catalisador. Suponhamos que a velocidade com que o reagente A desaparece na superfície catalítica seja dada por:
Considerando o processo de transferência de massa em regime permanente e a T e P constantes e que a reação ocorra sobre uma superfície plana do catalisador, determine o perfil da fração molar e o fluxo molar do soluto “A” em função da espessura da película gasosa “”.
Passo 1
Temos uma superfície catalítica, estilo plana plana, onde ocorre a reação:
E essa reação não é instantânea, nosso enunciado pede pra gente o perfil da fração molar e o fluxo molar, sendo a pressão e a temperatura constantes. Nossa solução deve obedecer a seguinte equação:
Fazendo as considerações necessária, vamos ter:
Como estamos trabalhando em regime permanente, então: ;
O fluxo de , vai ser apenas na direção , então: ∇;
E como não temos reação química homogênea, logo:
Com essas considerações nossa equação, vai ficar com essa cara aqui:
Logo, o fluxo total até a superfície do catalisador fica:
E pela estequiometria da nossa reação, temos:
E substituindo isso ali em cima, vamos ter:
Arrumando essa equação, teremos:
Ficamos então com:
E como vimos que , ficamos com:
E como nosso enunciado disse que temos pressão e temperatura constantes, nosso e , também vão ser constantes, logo:
Integrando isso aí, vamos ficar com:
E integrando novamente:
Ficaremos então, com:
Passo 2
Até aqui nada era muito novo porque a gente já tinha visto nos outros exercícios, né? Mas agora nossas condições de contorno mudaram… Vamos lá ver o que vai acontecer de diferente!
A nossa primeira condição de contorno é que:
Em:
Temos então:
Sendo assim:
E usando a segunda condição de contorno, como não temos uma reação instantânea, será:
Em:
Isso quer dizer que:
Substituindo o que já encontramos, ficaremos com:
O será então:
Agora vamos substituir e na equação que a gente tinha antes, ficaremos com:
Dividindo todos os termos por 2 e rearranjando, temos:
E multiplicando por , para trocar o sinal de todo mundo:
Aplicando agora a regra de logaritmos nessas subtrações:
E aplicando a regra do peteleco, ficamos com:
Tirando os logaritmos da jogada, teremos finalmente, o perfil da fração molar, sendo ele:
Agora partiu achar o fluxo !
Passo 3
Se a gente considerar um fluxo constante sobre a superfície do catalisador, vamos ter:
contante
Integrando a gente vai ficar com:
Nosso fluxo, será então:
Tranquilo? Arrasamos!
Resposta
Perfil da fração molar:
Fluxo de :
Exercício Resolvido #6
USP - Fenômenos de Transporte III - Professor Gerônimo
Uma partícula de carbono em forma de esfera queima no ar através da seguinte reação química:
A reação na superfície do carbono é descrita como sendo irreversível e de primeira ordem:
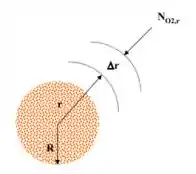
Considerando que o processo de transferência de massa ocorra em regime permanente e a e constante, determine o perfil de fração molar do oxigênio em função do raio da partícula esférica e o fluxo molar do oxigênio na superfície da partícula de carbono.
Passo 1
Bom, como a nós temos uma partícula que é esférica vamos usar a equação em coordenadas esféricas, ok? Olha ela aqui:
Fazendo algumas considerações…
Como estamos trabalhando em regime permanente, então: ;
O fluxo é radial e unidirecional, então: ∇;
E como temos um meio difusivo e não reacional:
Com essas considerações nossa equação, vai ficar com essa cara aqui:
A equação reacional é:
![]()
Temos então:
Como C é sólido, então:
E tendo a partícula estagnada, então:
Sendo assim, ficamos com:
Logo, o fluxo total de , em meio gasoso, fica:
E se , então ficamos com:
E substituindo isso ali em cima, vamos ter:
Como o enunciado disse pra gente que estamos trabalhando com pressão e temperatura constantes, então sabemos que e também são constantes, a equação vai fica então:
Integrando isso aí, vamos ficar com:
E integrando novamente:
Ficaremos então, com:
Passo 2
Agora é a hora de estabelecer nossas condições de contorno, pra que a gente descubra quem são e …
A nossa primeira condição de contorno é que:
Em:
Temos então:
Sendo assim:
E usando a segunda condição de contorno:
Em:
Isso quer dizer que:
Substituindo o que já encontramos, ficaremos com:
O será então:
Agora vamos substituir e na equação que a gente tinha antes, ficaremos com:
Rearranjando, temos:
O perfil da fração molar, será então:
Agora partiu achar o fluxo !
Passo 3
Se a gente considerar um fluxo total constante em , vamos ter:
constante
Sendo a área da esfera, ficaremos com:
constante
Agora vamos multiplicar a equação que a gente tinha antes pela área da esfera:
Ficaremos com:
Integrando a gente vai ficar com:
Nosso fluxo, será então:
Show de bola! E a gente ainda pode substituir o fluxo no perfil de fração molar e ficar com:
Reorganizando e fazendo as simplificações necessárias, ficamos com:
Logo, nosso perfil de fração molar ficará:
Prontinhos! Terminamos!
Resposta
Perfil da fração molar:
Fluxo:
Exercício Resolvido #7
USP - Fenômenos de Transporte III - Professor Gerônimo
Uma corrente gasosa contendo um reagente “A” entra em contato com um catalisador de geometria esférica de raio R. Esta partícula está dentro de um reator catalítico. Nas imediações da partícula catalítica, a concentração do reagente “A” é (moles/cm3 ). A espécie “A” difunde através dos poros existentes no catalisador e converte no produto “B” através de uma reação irreversível e de primeira ordem no sítio ativo do mesmo. O produto “B” difunde no sentido contrário do reagente “A”. Determine o perfil de concentração do reagente “A” em função do raio da partícula considerando que o processo de transferência de massa ocorra em regime permanente e a temperatura e pressão constante.
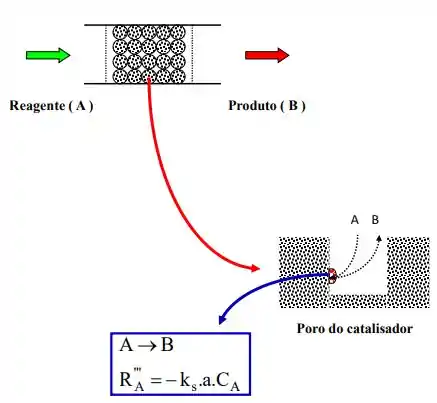
Sendo:
área da superfície catalítica por unidade de volume do catalisador
constante de velocidade
concentração do reagente
Passo 1
Mais uma vez vamos trabalhar com a equação em coordenadas esféricas:
Fazendo nossas considerações…
Como estamos trabalhando em regime permanente, então: ;
O fluxo é radial e unidirecional, então: ∇;
E considerando que a reação acontece dentro do poro do catalisador, temos que:
Sendo assim nossa equação, fica:
O fluxo molar no interior da parte porosa, levando em conta o coeficiente de difusão efetiva, , será:
Sendo:
Onde porosidade do catalisador e tortuosidade do catalisador.
E sendo , nossa equação será:
Agora substituindo isso na equação ali de cima, vamos ter:
Como o enunciado disse pra gente que estamos trabalhando com pressão e temperatura constantes, então sabemos que também é constante, ficamos então com:
Chamando , teremos:
Precisamos encontrar um jeito de melhor essa equação, porque esse vai nos atrapalhar nas integrações, ok? Vamos fazer o seguinte então:
Teremos então que:
Substituindo isso na nossa equação, ficaremos com:
Integrando isso aí, duas vezes, vamos ficar com:
Agora voltando com o , vamos ter:
Passo 2
Agora é a hora de estabelecer nossas condições de contorno, pra que a gente descubra quem são e …
A nossa primeira condição de contorno, se refere a entrada do poro, onde:
Temos então:
E usando a segunda condição de contorno, que se refere ao centro da partícula catalítica, temos:
Isso quer dizer que temos:
O será então:
Agora vamos substituir lá na primeira condição de contorno, beleza?
Logo, o vai ser:
Agora substituindo e na equação que a gente tinha antes, ficaremos com:
Por fim, rearranjando essa galera, o perfil de concentração do reagente “A” em função do raio da partícula será:
Uhull! Conseguimos!
Resposta
O perfil de concentração do reagente “A” em função do raio da partícula:
Exercício Resolvido #8
USP - Fenômenos de Transporte III - Professor Gerônimo
Um certo gás é dissolvido em um líquido B contido em uma proveta. Na medida em que A difunde ele sofre reação química na forma , até desaparecer completamente depois de penetrar a uma distância desde a interface gás/líquido. Considerando:
- a cinética de reação é de ordem zero com respeito a A;
- reação química lenta ;
- a concentração do gás A dissolvido é pequena se comparada ao do líquido B;
- o produto da reação L é altamente solúvel no líquido, o que leva a não influenciar na difusão do soluto A; obtenha expressões para:
- A distribuição da concentração molar de A;
- O fluxo global molar de A na interface gás/líquido;
- A concentração média molar de A.
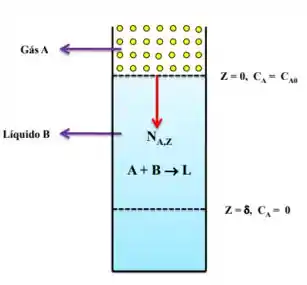
Passo 1
Precisamos calcular a concentração molar de em função de … A equação será:
Fazendo nossas considerações…
Como estamos trabalhando em regime permanente, então: ;
O fluxo é radial e unidirecional, então: ∇;
E considerando que a reação acontece dentro do poro do catalisador, temos que:
Sendo assim nossa equação, fica:
O fluxo total até a superfície do catalisador fica:
Se a gente considerar que a concentração do reagente A, é muito pequena em relação ao reagente B no meio reacional, podemos desprezar a parte convectiva do fluxo molar, ficando com:
E substituindo isso lá na nossa primeira equação, vamos ter:
E sendo a pressão e temperatura constantes, nosso , também vai ser constante, logo:
Chamando , teremos:
Integrando isso aí, vamos ficar com:
E integrando novamente:
Ficaremos então, com:
Passo 2
Agora é a hora de estabelecer nossas condições de contorno, pra que a gente descubra quem são e …
A nossa primeira condição de contorno, será na interface gás/líquido, onde:
Temos então:
Isso nos diz que:
E usando a segunda condição de contorno, que é quando o soluto é totalmente consumido, temos:
Isso quer dizer que temos:
Substituindo o , vamos ter:
O será então:
Agora substituindo e na equação que a gente tinha antes, ficaremos com:
Por fim, como estamos trabalhando com uma reação química lenta, então , e rearranjando essa galera, a distribuição da concentração molar do reagente “A” será:
Passo 3
Partiu encontrar o fluxo molar! Ele vai ser dado pela equação:
E se a gente voltar lá na equação:
E derivar ela em função de , vamos ter:
E como estamos buscando o fluxo na interface gás/líquido, , temos:
E substituindo isso na equação do fluxo, vamos ficar com:
E como , por ser uma reação lenta, temos que o fluxo molar será:
Passo 4
Só falta a gente encontrar a concentração média molar… Temos que:
Substituindo a nossa equação , vamos ter:
Isso nos dá:
E como a gente já falou antes, , logo a concentração média molar é:
Arrasamos! Foi grande, mas conseguimos!
Resposta
A distribuição da concentração molar do reagente “A”:
O fluxo molar:
A concentração média molar: