Exercícios de Diagrama de Moody e fator de atrito - Lista de Exercícios Resolvida

Sobre o Diagrama de Moody, analise as seguintes afirmações e afirme se são verdadeiras ou falsas.

I – O Diagrama de Moody é útil para a estimação do fator de atrito a partir do número de Reynolds e da rugosidade relativa tanto para escoamentos laminares como para escoamentos turbulentos.

II – Considerando dois escoamentos em tubos com o mesmo número de Reynolds, aquele com maior rugosidade relativa terá maior fator de atrito.

III – Em tubos lisos, o fator de atrito é zero, pois a rugosidade relativa é nula.

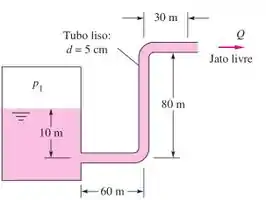
O escoamento no tubo da Figura é produzido pelo ar pressurizado no reservatório. Que pressão manométrica é necessária para fornecer uma vazão de água a 20°C?

Água a 20°C escoa por 10 m de tubo liso de 0,05 m de diâmetro a uma velocidade média de 8 m/s. Calcule a perda de carga em metros.

Querosene a é bombeado apor de tubo horizontal de ferro fundido de de diâmetro. Calcule a potência necessária de entrada em , se as bombas têm de rendimento.

O escoamento de água a 20°C ocorre em regime de turbulência completa em um tubo de 0,02 m de diâmetro de aço inoxidável novo. Calcule o fator de atrito.

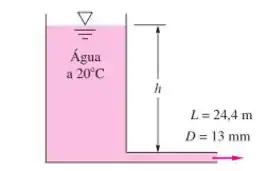
Qual nível deve ser mantido na Figura para fornecer uma vazão de pelo tubo de aço comercial de de diâmetro?

Mercúrio a escoa por de tubo de vidro dede diâmetro a uma velocidade média de . Calcule a perda de carga em metros e a queda de pressão em .

Os dados a seguir foram obtidos para o escoamento de de água a por um tubo com forte corrosão, de de diâmetro, que está inclinado para baixo a um ângulo de : , , , . Calcule (a) a rugosidade relativa do tubo e (b) a variação percentual na perda de carga se o tubo fosse liso e a vazão a mesma.