Introdução aos Fluidos
Produzido por Raphael EloiTeoria
O que é fluido?
De maneira simples e direta, podemos dizer que a matéria pode estar no estado sólido, no estado líquido ou no estado gasoso e que esses dois últimos são fluidos. Então fluido é meio que o contrário de sólido, beleza? Existem também outros estados da matéria, umas paradas mais complicadas, tipo o plasma, mas não vamos falar disso aqui ok?
Agora eu te pergunto: você saberia explicar o que é um líquido ou um gás? E o que diferencia um deles de um sólido?
“Ah, fácil, fluido é tudo que não é sólido!” ou “é aquilo que assume a forma do recipiente em que está”. Será?
E aquelas geleias que as crianças brincam: são fluido ou sólido?

Aí a pergunta já não é tão trivial, né? Por isso vamos estabelecer alguns conceitos básicos e definições.
Quando a gente fala que aquele jogo, aquela prova, ou aquele papo fluiu, é uma coisa boa, né? Aqui em MecFlu, fluir é sinônimo de escoar. Então um fluido é algo que escoa!
Agora pensa numa gota de óleo sobre uma superfície horizontal. Ela não tá escoando. Você inclina um pouco a superfície e ele segue parada. Inclina mais e nada. Mais um pouco. Mais um pouco... e de repente a gota começa a escoar.
O que isso significa? Quando ela tava parada ela era sólido e com um plano bem inclinado ela virou fluido? Não né! Mas isso nos mostra que precisamos de uma definição mais específica do escoamento do fluido. Como ele acontece? Precisa aplicar uma força? Quão forte? Sólidos não vão escoer?
Quando questionamos as definições mais básicas, as coisas que pareciam óbvias começam a ficar bem menos bobas! Eu também senti isso. Mas fica tranquilo e vem comigo, porque já já você vai conhecer melhor os fluidos que estamos estudando.
Então, um fluido é toda matéria que ao receber a ação de uma tensão cisalhante (traduzindo: uma tensão que atua paralelamente ao movimento) irá escoar continuamente, até que a resultante dessa tensão volte a ser zero. Não importando o quão pequena seja essa tensão.

Tá vendo, sobre a ação daquele o fluido tá se deformando cada vez mais.
Agora dá uma olhada no sólido.

Pra uma dada tensão, ele se deforma e “para”. Pra deformar mais, você vai ter que aplicar mais tensão. E se você tirar essa tensão, ele volta ao estado normal dele.
Já o fluido, este vai fluir... Isso mesmo, ele irá escoar. Por que isto ocorre? Bem, a explicação disso deve-se às forças intermoleculares (Química, ame-a ou deixe-a. Foi mal a galera que gosta de química, mas eu deixei! haha)
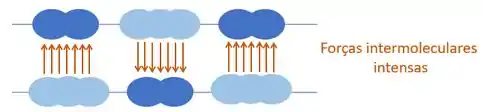
Em um sólido, as forças entre as moléculas são grandes. Por isso, quando a gente aplica uma tensão, a gente até pode deslocar uma camada de moléculas sobre a outra, mas a força intermolecular entre as camadas vai “segurar” aquela camada que a gente tá empurrando, fazendo com que o material pare de se deformar.
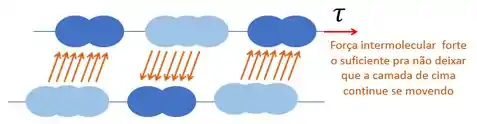
Já no fluido essa força intermolecular é fraca. Aí, quando uma camada recebe tensão, a camada seguinte não tem força para parar o movimento e, assim, aquela camada “escorrega”: o fluido escoa.
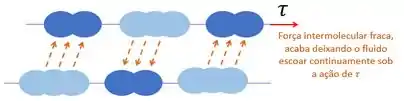
Em química a galera estuda mais a intensidade das forças intermoleculares de acordo com as substâncias e tal. Pra gente aqui, basta saber que são essas forças que fazem com que a matéria seja um sólido ou um fluido.
E em Mecânica dos Fluidos a gente estuda os fluidos (surpresaaaa) que, como a gente viu, serão gases ou líquidos.
Massa específica, Densidade, Volume específico e Viscosidade
Agora que já aprendemos o que é um fluido, vamos aprender a caracterizar esses caras.
Pra você entrar no clima, imagina que você descobriu a vocação da sua vida: fazer cerveja! No final do processo de produção de cerveja, você obteve 5 kg de cerveja e tem que colocar ela em garrafas. Mas pra saber a quantidade de garrafas que você vai precisar, não adianta nada você saber o peso de cerveja que você tem. Você precisa saber quantos litros você produziu, ou seja, o volume de cerveja produzido.

E aí, o que você faria? Como engenheiros, procuramos pela solução mais rápida e barata. Tipo uma única conta que resolva esse problema né?! Alguma coisa que relacione a massa e o volume de cerveja. Opa, parece que estamos falando de massa específica!
Massa específica ()
Massa específica de um fluido é a razão entre a massa de um fluido e o volume que ele ocupa.
Podemos definir matematicamente como:
Então agora você pode procurar na internet a massa específica da cerveja e descobrir qual o volume ocupado por 5 kg de cerveja. Seus problemas acabaram!
A massa específica é relativo à uma substância e pode variar de acordo com a temperatura e a pressão.
Densidade Relativa (d)
Por que não comparar a massa específica dos líquidos com o líquido mais famoso, a água? Ou comparar a de um gás com a do ar?
Essa comparação pode ser bem útil, porque te ajuda a visualizar o problema. Tipo assim, se eu te disser que a massa especifica do mercúrio é , talvez isso não te ajude a visualizar se ele é muito denso ou não. Mas se eu te disser que a massa especifíca do mercúrio é vezes a da água, aí você já tem um meio de comparação e consegue meio que “enxergar” que o cara é bem denso.
Por isso vamos usar a comparação e é daí que surge a densidade relativa. A densidade relativa é a comparação entre a massa específica de um fluido com a massa específica de um fluido de referência. Normalmente usamos a água como fluido de referência para líquidos e o ar como fluido de referência para gases.
Outra parada importante é que a densidade relativa é admensional. Então vai ser assim: “ a densidade do mercúrio é ”.
Normalmente usamos a massa espefícica da água igual a ou e a do ar como ou . Mas isso vai depender da temperatura e da pressão. Consequentemente, a densidade relativa também vai depender da temperatura e da pressão, falou?
Volume específico ()
Lembra que pra massa específica a gente divide massa por volume? Bem, pro volume específico a gente vai dividir volume por massa. E é só isso mesmo, o volume específico é o inverso da massa específica. Dá uma olhada aí.
O volume específico é a razão entre o volume de uma substância e a massa de substância. Ele é uma característica da substância e também depende de temperatura e pressão.
Viscosidade
Fala tu, quem é mais viscoso: o óleo ou a água?
Óleo é a resposta correta e também a mais intuitiva. É fácil “intuir” que é o óleo, mas você saberia definir porque você “escolheu” o óleo? Consegue definir viscosidade?
O óleo é mais viscoso porque ele oferece mais resistência ao escoamento.
Agora outro exemplo. Já tentou dar um soco dentro da água? E no ar? Pra qual deles você precisa fazer mais força?

Você precisa fazer mais força pra dar um soco na água porque ela tem maior resistência ao movimento do que o ar.
A essa resistência ao movimento associamos a viscosidade.
Em resumo: a viscosidade é a resistência que o fluido tem para fluir (escoar).
A viscosidade tem a ver com o atrito interno do fluido, entre as diferentes camadas de moléculas que formam ele. Se tem muito atrito, você precisa de mais força pra mover uma camada sobre a outra e o fluido se é mais viscoso.
E a viscosidade varia com a temperatura e a pressão?
Quando a temperatura e a pressão variam, o movimento relativo das moléculas e o quão “soltas/presas” elas estão umas das outras também muda. Então sim, a viscosidade varia com a temperatura e a pressão. Mas como?
A viscosidade de líquidos e gases vai variar de maneira diferente em relação à T e P.
Vamos começar pelos líquidos.
Em geral, a ação da pressão é muito pequena na viscosidade dos líquidos. Mas a temperatura tem bastante influência.
Quando aumentamos a temperatura, as moléculas do líquido passam a vibrar mais. Vão ficando mais “soltinhas” uma das outras. Assim, caso a gente aplique uma tensão, elas escoam mais facilmente. Em outras palavras: quanto maior a temperatura, menor a viscosidade.
Se você já aqueceu um pouco de óleo numa frigideira, você vai lembrar que quando a frigideira tá bem quente o óleo fica “super líquido”, bem menos viscoso.
E pros gases?
Bem, pros gases a história é outra. Nos gases as moléculas já estão super soltas no espaço. Aumentar a temperatura vai aumentar o grau de agitação médio das moléculas e, consequentemente, o número de colisão entre elas. Com mais colisões, o fluido escoa com mais dificuldade. Ou seja: fica mais viscoso.
Então, para os gases, quanto maior a temperatura, maior a viscosidade.
Agora, se aumentarmos a pressão, as moléculas do gás ficam mais juntinhas, se chocam mais e a viscosidade aumenta também.
Pra guardar no coração:
ATENÇÃO! Não pense que o atrito dos gases é maior que o dos líquidos por causa das colisões entre as moléculas, ok? Na verdade o atrito dos gases é bem menor que o dos líquidos, pelo fato de nos gases as partículas estarem “soltas”. Já nos líquidos elas estão são mais ligadas, então as camadas de moléculas estão sempre “se esfregando” umas nas outras. O “atrito interno” dos gases é bem menor do que nos líquidos e, por isso, gases são bem menos viscosos.
Viscosidade cinemática
Existem dois tipos de viscosidade, conhecidas por viscosidade dinâmica e viscosidade cinemática.
A viscosidade dinâmica também é chamada de viscosidade absoluta ou só viscosidade mesmo. Para essa daí a gente usa o (“mi”) e, no SI, usamos como unidade. Outra unidade muito usada é o Poise, indicado pela letra ou o centipoise (). Se liga aí nas conversões:
E a viscosidade cinemática nada mais é do que a viscosidade absoluta dividida pela massa específica do fluido. Nós usamos a letra grega (“ni”) para representar ela, ok?
No SI, a unidade dela é , mas a unidade mais usada é Stokes (). E pra fazer a conversão:
Vimos muita coisa, algumas novidades então nada melhor que fazermos alguns exercícios para por em prática o que aprendemos, ver se não ficou nenhuma dúvida ou mal entendido e ver algumas dicas. Que venham os exercícios então!
Massa específica, Densidade, Volume específico e Viscosidade
Massa específica ( ρ )
Densidade Relativa (d)
Volume específico ( υ )
Viscosidade
E a viscosidade varia com a temperatura e a pressão?
Viscosidade cinemática
Exercícios Resolvidos
Exercício Resolvido #1
Lista de exercícios – Fenômenos de transporte
Um cubo cuja aresta é possui massa igual a . Qual é a massa específica desse cubo?
Passo 1
A massa específica é massa sobre volume:
A massa foi dada pelo problema:
Agora precisamos calcular o volume.
Passo 2
O volume do cubo de aresta é dado por
O problema nos diz que
Logo:
Passo 3
Substituindo:
Resposta
Exercício Resolvido #2
Elaboração própria
Um óleo de densidade foi escolhido pelos estudantes de um projeto para lubrificar um motor. Qual a sua massa específica?
Passo 1
Olá! Esse é um exercício para calcular a massa específica , sendo que nossos amigos, estudantes como nós, já sabem a densidade do fluido.
Ué! Eles já sabem a densidade. Então essa já não é a massa específica?
Então! Massa específica e densidade são variáveis que tem a ver uma com a outra, mas não são exatamente a mesma coisa em MecFlu! Relaxa, no começo pode parecer confuso, mas vem comigo que agora você tira essa dúvida!

Muitas vezes usamos no nosso dia a dia o termo densidade quando na verdade queremos dizer massa específica. Tudo bem, isso é comum. Mas a dica de ouro para você não se enrolar mais com esses termos daqui para frente é:
Fica atento às unidades!
Repara que o enunciado deu a densidade e ela está sem unidade! O que isso significa? Que essa densidade é a densidade relativa, essa querida aqui:
E quem é o numerador dessa equação? Sim, a própria massa específica que queremos saber!
Então vamos substituir o que foi dado? Sabemos que
Além disso, vamos considerar que (esse valor vai andar sempre com a gente por aqui em MecFlu!). Estou usando a massa específica no Sistema Internacional, hein! A unidade é kg/m³.
Então:
Passando para o outro lado:
E encontramos a massa específica que os estudantes precisavam! Partiu próximo exercício? o/
Resposta
Exercício Resolvido #3
Elaboração própria
Uma piscina está completamente cheia de um determinado fluido. Sabe-se que a massa de fluido utilizada para enchê-la totalmente foi de . As dimensões da piscina são: . Calcule (a) a massa específica do fluido. (b) a densidade relativa do fluido. Utilize o sistema internacional.
Passo 1
Eu gosto de estudar exatas porque essa alegria de poder calcular o volume da piscina que eu vou curtir no rolê é incomparável! HAHAHA

Brincadeiras a parte, esse exercício é legal porque vai consolidar o que aprendemos dessas variáveis que vão nos acompanhar sempre em MecFlu: massa específica e densidade relativa.
É muuuito importante lembrar que são conceitos relacionados um com o outro, mas são diferentes!
Vamos começar com a massa específica. Ela é a divisão entre massa e volume. Olha aí:
A massa para preencher toda a piscina sabemos que é pelo enunciado. Então:
E quanto ao volume? Sabemos que a piscina está completamente cheia e sabemos as dimensões da piscina. Então vamos multiplicar base, largura e profundidade para encontrar o volume que esse fluido está ocupando:
Como o fluido está ocupando a piscina toda, o volume do fluido é o volume da piscina toda 😉
E assim
Opa, então voltando na definição da massa específica:
E assim encontramos a massa específica do fluido no Sistema Internacional já!
Passo 2
E como faz para encontrar a densidade relativa? Vamos lembrar de como ela foi definida:
A densidade relativa é a razão entre a massa específica do fluido e a massa específica da água. é um valor de referência e costumamos usar
E acabamos de calcular no passo anterior. Bora substituir?
As unidades em cima e embaixo são as mesmas, então fazendo as contas, encontramos:
Isso mesmo, a densidade relativa é 1,03. Sem unidades mesmo! E assim encontramos a resposta final!
A massa específica é medida em kg/m³ no Sistema Internacional e a densidade relativa não tem unidade em sistema nenhum porque não tem dimensão. 😊
Resposta
Exercício Resolvido #4
Lista de exercícios MecFlu UFJF.
(Adaptada) Qual é o valor do volume específico em , de um líquido cuja densidade vale 0,8.
Passo 1
Tá vendo que a densidade dada não tem unidade? Então essa é a nossa unidade relativa.
Então vamos precisar transformar essa densidade relativa em massa específica e depois calcular o volume específico, que nada mais é do que o inverso da massa específica. Bora então?
Passo 2
Pra densidade relativa:
Como a substância de referência não foi dada, vamos assumir que é a água. Se o fluido estudado fosse um gás, a gente ia assumir que o fluido de referência era o ar, ok?
Então fica assim:
Como queremos a resposta final em , já vamos usar a unidade certa né?
Passo 3
Com a massa específica nas mãos, fica fácil de calcular o volume específico:
Resposta
Exercício Resolvido #5
Um fluido tem viscosidade igual a e massa específica . Determinar sua viscosidade cinemática.
Passo 1
Vimos na teoria que a viscosidade cinemática é dada pela razão entre viscosidade e massa específica. Então:
Esse é o valor da viscosidade cinemática.
Antes de correr pro abraço, dá só uma confirmada nas unidades, valeu? Aqui foi de boas porque tudo já estava no SI mesmo!
Resposta
Exercício Resolvido #6
A viscosidade absoluta de um fluido é principalmente uma função da:
Massa específica
Temperatura
Pressão
Velocidade
Tensão Superficial
Passo 1
Essa é uma daquelas questões que a maioria das pessoas só sabe a resposta se já viu a questão antes. E como a gente já viu, a gente compartilha ela com você!
Bem, como o enunciado da questão anterior nos disse, a viscosidade é fixada em função do estado termodinâmico da substância.
E em termodinâmica as principais características são pressão e temperatura. Sendo a temperatura o estado que mais influencia os outros, pois ele que diz a energia e velocidade médias das moléculas.
Por isso, a viscosidade é função principalmente da temperatura.
Passo 2
Bem, mas se não soubéssemos disso teria como fazer a questão? Teríamos que ir eliminando alternativa por alternativa. Vamos então dar uma olhada em cada uma delas.
Primeiro a massa específica. A massa específica é fixa para um determinado fluido em dadas condições de T e P. E não faz sentido falar que a viscosidade é principalmente função de algo fixo.
Passo 3
Vamos pular para a velocidade. Será que se eu pegar um fluido muito viscoso e variar a velocidade de escoamento dele, a viscosidade desse cara vai mudar?
Bem, isso me parece meio controverso. Pelo menos para mim, intuitivamente, parece que é o contrário: a viscosidade que vai influenciar na velocidade de um fluido. Tipo fazer um líquido pouco viscoso escoar me parece mais fácil do que um muito viscoso.
Passo 4
Agora vamos eliminar a tensão superficial. Sempre que se fala de tensão superficial eu lembro da imagem do mosquito em cima da água. E me lembro de ouvir falar disso quando estava estudando forças intermoleculares e coisas do tipo. Não vejo como a tensão superficial iria influenciar no atrito interno de um fluido. Ao menos não como essa teria uma “influência principal”.
Passo 5
Ae seria o momento crucial: pressão ou temperatura.
Ambas são propriedades termodinâmicas e ambas podem influenciar na viscosidade.
E agora, papito? Bem, na teoria vimos falar da variação da viscosidade quanto à temperatura e muito pouco sobre a pressão. Então vamos contar um ponto para a temperatura. Além disso, pra pressão ter uma influência na viscosidade, ela tem que variar muito. Mas como eu sei disso?
Bem sabemos que quando subimos ou descemos estamos mudando a pressão, tipo a pressão no Rio de janeiro é muito maior que no Everest. Nunca fui no Everest, mas já fui em alguns lugares altos e percebi o ar mudar muito com a pressão. O mesmo vale para quando mergulhamos, a cada metro mais profundo maior é a pressão e não vejo grande variação na viscosidade.
Agora a temperatura muda muito as coisas. Quem nunca viu mel, ou algum fluido viscoso ser esquentado e depois disso fluir muito mais facilmente?
Por isso, poderíamos escolher a temperatura como principal característica.
Resposta
Alternativa
Exercício Resolvido #7
Prova CESGRANRIO 2011 para Engenheiro de Petróleo Júnior.
A viscosidade é uma propriedade dos fluidos relacionada a forças volumétricas de atrito interno que aparecem em um escoamento devido ao deslizamento das camadas fluidas, umas sobre as outras. Para um fluido newtoniano, a viscosidade é fixada em função do estado termodinâmico em que o fluido se encontra. A propriedade que mais influencia na viscosidade de líquidos e gases é a temperatura. Para a maioria dos fluidos industriais, à medida que a temperatura aumenta, a viscosidade:
dos líquidos e a dos gases aumentam.
dos líquidos e a dos gases diminuem.
dos líquidos aumenta, e a dos gases diminui.
dos líquidos diminui, e a dos gases aumenta.
dos líquidos diminui, e a dos gases não sofre alteração.
Passo 1
O próprio enunciado dá uma explicada sobre o conceito de viscosidade. Além disso, como vimos na teoria ele ainda relaciona com um atrito interno perante o deslizamento.
E na teoria vimos que, nos líquidos, ao aumentarmos a temperatura as moléculas se agitam mais, o que deixam elas mais solta e diminui atrito entre as camadas de moléculas. Ou seja, diminui a viscosidade.
Se você ainda não entendeu muito bem porque isso ocorre. Lembre do atrito estático e cinético que vimos na física. O estático é maior que o cinético. O mesmo ocorre nos líquidos, o atrito entre uma camada e outra de molécula diminui quando a vibração delas aumenta e isso ocorre quando a temperatura do líquido aumenta.
Passo 2
Só que o aumento de temperatura (aumento de vibração das moléculas) tem um efeito contrário nos gases: aumenta a viscosidade.
Pois a maior energia fornecida às moléculas vai aumentar a velocidade delas e, assim, aumentar o número de choques entre elas. E se há mais choques há mais atrito.
Resumindo então temos que, aumento de temperatura nos:
Assim escolheremos a
Resposta
Exercício Resolvido #8
A viscosidade é a propriedade associada à resistência que o fluido oferece à deformação por cisalhamento. Explique conceituando o que é viscosidade dinâmica do fluido.
Passo 1
Ih rapaz, viscosidade dinâmica?
Calma, falamos disso brevemente na teoria: dissemos que viscosidade dinâmica é a viscosidade que nos referimos normalmente.
É a mesma coisa que viscosidade absoluta ou só viscosidade que conceituamos como a resistência que o fluido tem a escoar.
Pra responder a esse exercício, vamos ter que fazer uma analogia entre a deformação dos fluidos e a dos sólidos elásticos que estudamos lááá na física. Calma aí que nós vamos fazer isso juntos!
Passo 2
Viscosidade é a relação entre a força de cisalhamento aplicada e a deformação sofrida pelo fluido.
Lembra da lei de Hooke, que nos dizia que a deformação do corpo dependia da força aplicada e da constante elástica do corpo? Assim ó:
Então a viscosidade teria um papel semelhante ao da constante elástica. Dada uma força, ela que define o quanto o fluido vai se deformar/escoar. Por analogia, podemos escrever algo como:
Onde é a tensão de cisalhamento, a viscosidade e é a taxa de deformação.
Essa equação é conhecida como lei de Newton e por isso os fluidos que respeitam ela são conhecidos como fluidos newtonianos.
Mas relaxa. Nesse início vamos focar no estudo da estática dos fluidos e a viscosidade não será estudada tão a fundo. Mais pra frente voltaremos a falar dela.
Resposta
Ei, a resposta está no passo a passo :)