Tensão cisalhante e tipos de fluidos
Produzido por Raphael EloiTeoria
A tensão de cisalhamento é uma força gerada por forças aplicadas em sentidos iguais ou opostos. Muitas vezes a gente vê a tensão de cisalhamento aplicada em objetos sólidos, mas hoje vamos ver o que acontece quando aplicamos uma tensão de cisalhamento em um fluido!
Tensão de Cisalhamento em Fluidos
A tensão de cisalhamento é a tensão gerada pela atuação de uma força paralela ao movimento em uma superfície onde temos um fluido. Então, quando o fluido é submetido a uma tensão cisalhante, por menor que ela seja, ele não resiste!

Quando a tensão cisalhante
A taxa de deformação
Mas ai você me pergunta: Existe alguma equação que rege esse movimento?
Sim! É a Lei de Newton da Viscosidade, que vamos conhecer agora!
Lei de Newton da Viscosidade
A Lei de Newton da Viscosidade nos ajuda a calcular a tensão cisalhante
Onde:
é a tensão cisalhante, medida em ; é a viscosidade em ; é a taxa de deformação.
-Beleza, mas como eu acho a taxa de deformação? A questão vai me dar?
Geralmente a questão vai te dar o perfil de velocidade
Bora ver um exemplo de como achar o perfil de velocidade?!
Exemplo: Encontre a taxa de deformação
Sabendo que o perfil de velocidade do escoamento de um fluido sobre uma superfície é dado por:
Onde
Para encontrarmos a taxa de deformação, tudo o que precisamos fazer é derivar o perfil de velocidade com relação a
Substituímos as constantes:
Organizando a casa:
Prontinho!
Fluidos Newtonianos
Os Fluidos Newtonianos são aqueles que obedecem a Lei de Newton da Viscosidade, como por exemplo a água, o álcool, a gasolina.
A gente viu, que pela lei de Newton da viscosidade, existe uma relação linear entre a tensão de deformação e a taxa de deformação do fluido. Isso significa que a medida que eu aumento a tensão, a taxa de deformação aumenta de forma linear e proporcional à viscosidade. Para um fluido ser Newtoniano ele deve ter esse comportamento!
-Mas não são todos os fluidos que se comportam dessa forma?
Na verdade não, olha só os outros tipos de fluidos que existem:
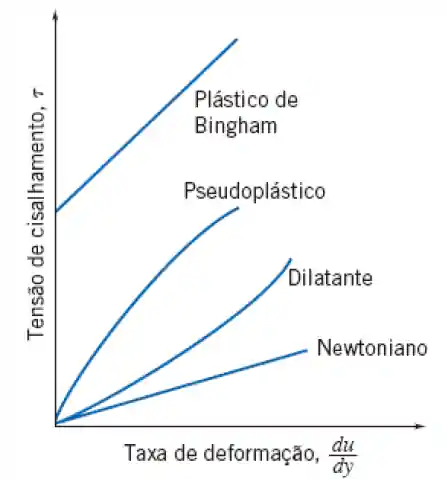
No gráfico acima podemos ver como diferentes fluidos se comportam quando aplicamos uma tensão de cisalhamento.
Existem vários fluidos não newtonianos no nosso dia a dia. Sabe quando você vai espremer um tubo de maionese, faz força, não sai nada e do nada sai um monte de maionese no seu sanduiche?
A maionese é um fluido não newtoniano, chamado de fluido de Bingham, nesse tipo de fluido você precisa aplicar uma tensão mínima pra ele começar a se mover!
Existem outros exemplos no nosso dia a dia, como a tinta que a gente usa pra pintar a parede, a pasta de dente e se você quiser fazer uma experiência em casa, mistura água com amido de milho e depois me conta o que aconteceu! 😉
Fluidos Compressíveis e Incompressíveis
Como o próprio nome sugere, o fluido compressível é o fluido que é possível comprimir, então se aplicarmos uma força nesse fluido conseguimos diminuir seu volume, certo? Isso quer dizer que sua massa específica é variável!
Agora, quando aplicamos uma pressão sob um fluido incompressível seu volume não varia, isso quer dizer que sua massa específica é constante.
É importante entendermos a diferença entre fluidos compressíveis e incompressíveis, porque aqui em MecFlu geralmente vamos considerar apenas fluidos incompressíveis, o que vai facilitar muito na hora das continhas! Mas também é importante saber quando podemos fazer essa aproximação ou não, combinado?
Agora pra fechar com chave de ouro, se liga nesse vídeo resumo sobre tensão de cisalhamento e tipos de fluidos que o Responde Aí preparou pra você!
Agora, vamos praticar com exercícios?
Fluidos Newtonianos
Fluidos Compressíveis e Incompressíveis
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Considere o gráfico de Tensão Cisalhante por taxa de deformação (taxa de cisalhamento) a seguir:
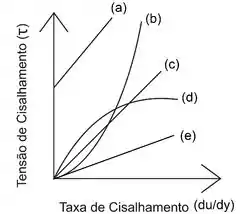
Cada curva representa um fluido diferente. Qual(is) dos fluidos são newtonianos? Por quê?
Passo 1
Opaa! Questão de gráfico! Afinal, como é que dá para saber se um fluido é newtoniano por esse gráfico aí?
Então, na teoria a gente viu que um fluido é newtoniano se ele obedece a lei de Newton da viscosidade, certo? Olha aí para gente lembrar:
No gráfico de tensão cisalhante (eixo y) por taxa de deformação (eixo x), acontece isso:
Logo, num gráfico desse tipo (como é no nosso enunciado), um fluido newtoniano seria representado por uma reta assim:
Repara que não é qualquer reta! É uma reta com coeficiente linear igual a zero, ou seja, ela começa na origem!
O próximo passo é ver quais das curvas do gráfico é descrita por uma reta
Passo 2
Lembrando do gráfico
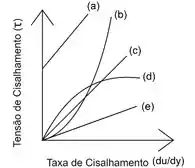
A curva (a) é uma reta, mas é uma reta com coeficiente linear diferente de zero, ou seja:
Logo, o fluido (a) não é um fluido newtoniano, pois para isso b teria que ser zero. Portanto, a curva (a) não representa um fluido newtoniano, mas sim fluido de Bingham!
Vamos falar da curva (b) agora? Essa curva não é linear! Não dá para ser descrita como uma reta... Então, o fluido (b) não é newtoniano. Esse é o tipo de curva que descreve um fluido dilatante.
E a curva (c)? Podemos ver que ela é linear, certo? Além disso, ela corta o eixo y na origem. Dá uma olhadinha! Então, por causa disso, essa curva ma-ra-vi-lho-sa pode ser descrita por uma reta do tipo
Então, o fluido (c) é newtoniano! 😉
Dá para ver que a curva (d) não é descrita por uma reta, certo? Aliás, esse tipo de curva descreve os fluidos pseudoplásticos.
E por fim, a curva (e) também é uma reta! Onde ela corta o eixo y? Na origem. Logo, é uma reta sem coeficiente linear. Então, por isso, o fluido (e) também é newtoniano!
Guarda aí: quando o gráfico da tensão cisalhante pela taxa de deformação é uma reta que passa pela origem, então o fluido é newtoniano!
Além disso, os tipos de fluido nesse gráfico são esses:

Resposta
Os fluidos newtonianos são os representados pelas curvas (c) e (e), pois obedecem à Lei de Newton da Viscosidade.
Exercício Resolvido #2
Em relação ao comportamento reológico de fluidos, analise as proposições a seguir.
A viscosidade de um fluido sempre diminui com o aumento da temperatura.
Fluidos nos quais a tensão de cisalhamento não é proporcional ao quadrado da taxa de deformação são ditos fluidos não newtonianos.
Um fluido plástico de Bingham não escoa quando submetido a uma tensão de cisalhamento inferior a um determinado valor limite.
Há fluidos não newtonianos nos quais a viscosidade aparente varia com o tempo.
São corretas APENAS as proposições
Passo 1
Vamos ter que analisar afirmativa por afirmativa.
A viscosidade de um fluido sempre diminui com o aumento da temperatura.
FALSA!
Pois vimos na teoria que isso depende se estamos falando de líquidos ou gases, que nos gases o aumento da temperatura aumenta a viscosidade.
Passo 2
Fluidos nos quais a tensão de cisalhamento não é proporcional ao quadrado da taxa de deformação são ditos fluidos não newtonianos.
FALSA. Fluidos não newtonianos são aqueles que a tensão de cisalhamento não é proporcional a deformação, ou seja, que a deformação não varia linearmente com a tensão de cisalhamento aplicada.
Passo 3
Um fluido plástico de Bingham não escoa quando submetido a uma tensão de cisalhamento inferior a um determinado valor limite.
VERDADEIRA.
Os fluidos de Bingham só escoam se sofrerem ação de uma tensão de cisalhamento maior que uma tensão de cisalhamento mínima.
Passo 4
Há fluidos não newtonianos nos quais a viscosidade aparente varia com o tempo.
Verdadeira.
Não falamos sobre isso, mas sabendo que a 3 é verdadeira e as outras não a única alternativa possível é
Mas então, existem sim fluidos em que a viscosidade varia com o tempo. Eles podem ser de dois tipos: fluidos tixotrópicos; fluidos reopéticos. Isso não cabe ao nosso estudo, mas se tiver curiosidade pesquise um pouco do comportamento deles é bem interessante.
Assim a alternativa correta é a letra
Resposta
Alternativa
Exercício Resolvido #3
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 76, ex. 2.43
(Adaptada) O perfil de velocidade de um fluido que escoa sobre uma superfície é definido por:
Sabe-se que o fluido é água a 20°C e que é a espessura do escoamento. Sendo , encontre a expressão para taxa de deformação .
Passo 1
E aí? Bora aprender a segurar esse forninho chamado perfil de velocidades?
Bem, a primeira coisa que você precisa saber para resolver esse tipo de questão é que por mais esquisito que o perfil de velocidade pareça, é a partir dele que você consegue achar a taxa de deformação.
Dica de amig@: esse perfil tem uma cara estranha, mas na verdade ele está tímido, escondendo sua tranquilidade! e são constantes. Quando substituirmos os seus valores, a equação vai ficar mais simples de se ver.
Como o fluido é a água a 20°C, sabemos que
Lembrando que:
E pelo enunciado:
Substituindo esses valores no perfil de velocidade:
O perfil de velocidade é um polinômio de segundo grau do bem. 😊
Passo 2
Para encontrar a taxa de deformação , precisamos derivar nosso perfil de velocidade em relação a y.
Derivando:
E assim encontramos a expressão para taxa de deformação! :D
Resposta
Exercício Resolvido #4
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 76, ex. 2.40
(Adaptada) A distribuição de velocidade para o escoamento laminar desenvolvido entre placas paralelas é dada por
em que é a distância separando as placas e a origem está situada na linha mediana entre as placas. Considere um escoamento de água a 20°C, com e . Calcule a tensão de cisalhamento na placa superior e dê o seu sentido.
Passo 1
Eu sei... esse enunciado pode parecer um pouco assustador de primeira, mas eu te trago ótimas notícias:
Finalmente chegou a sua hora de brilhar e calcular a tensão de cisalhamento! =D Tamo junto nessa!
E qual o segredo? Bem, para esse primeiro momento, vamos precisar da tensão cisalhante, da viscosidade e da taxa de deformação. Como se trata da água, que é fluido newtoniano, vale a Lei de Newton da Viscosidade:
Vejamos... a viscosidade da água a 20°C tem um valor certo. Além disso, o enunciado deu o perfil de velocidade. Então, para achar a tensão cisalhante, precisamos derivar esse perfil de velocidade aí em relação a y. Bora?
Passo 2
Vamos encontrar a taxa de deformação . Para isso, vamos derivar o perfil de velocidade, esse cara aqui:
Vamos derivar esse perfil em relação a . Mas antes vamos dar uma organizada nessa equação aí:
Agora sim! Lembrando que é a velocidade máxima e é uma constante. é a distância que separa as duas placas, então também é uma constante. Então, derivando u em relação a y:
Organizando melhor:
Bem, então se a gente souber o valor dessas constantes e , vamos finalmente conhecer a taxa de deformação . A boa notícia é: o enunciado já deu esses valores! São e .
Para substituir, precisamos passar tudo para o Sistema Internacional. A velocidade já está em metros por segundo. Só falta colocar a altura em metros:
Substituindo:
Opa! Encontramos a taxa de deformação!
Passo 3
Para achar a tensão cisalhante, vamos substituir a expressão que encontramos para a taxa de deformação na Lei de Newton da Viscosidade:
Substituindo:
Lembrando que a viscosidade da água é
Encontramos então uma expressão para a tensão cisalhante.
Passo 4
Calculamos a tensão cisalhante. Tá faltando alguma coisa? Repara que o enunciado pediu para calcular a tensão cisalhante na placa superior. Ou seja, precisamos substituir o que corresponde à posição da placa superior nessa expressão de que encontramos no passo 3.
Em matematiquês:
E quem é o ?
Voltando ao enunciado, lá diz que a “origem está na linha mediana entre as placas”. E lembrando que a distância entre as placas é . A figura ilustra a situação:

Repara que a gente definiu como “positivo” pra cima e pra direita 😉
Substituindo
Encontramos o que o exercício pediu! A tensão de cisalhamento na placa superior é .
Na figura vemos que o sentido positivo é para a direita. Como encontramos a tensão com sinal negativo, podemos concluir que o sentido da tensão é para a esquerda. Eu não falei que era seu momento de brilhar?

Resposta
Sentido: da direita para a esquerda
Exercício Resolvido #5
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 76, ex. 2.41
A distribuição de velocidade para o escoamento laminar desenvolvido entre placas paralelas é dada por
em que é a distância separando as duas placas; a origem está situada na linha mediana entre as placas. Considere o escoamento de água a 20°C com velocidade máxima de e . Calcule a força sobre uma seção de 1m² da placa inferior e dê o seu sentido.
Passo 1
Esse exercício tem o enunciado parecido com o anterior. Mas tem duas diferenças principais!
A primeira é que agora o exercício está pedindo a força ao invés da tensão de cisalhamento. Além disso, o valor da velocidade máxima mudou, agora é
Como resolver então? A estratégia vai ser parecida com a do exercício anterior, porém teremos mais um passo.
Primeiro, precisamos encontrar a taxa de deformação derivando o perfil de velocidade.
Depois, usando a Lei de Newton da Viscosidade (já que o fluido é newtoniano), vamos calcular a tensão cisalhante.
E como tensão é força sobre área, no último passo vamos calcular a força com essa fórmula:
Então vamos nessa!
Passo 2
Para encontrar a taxa de deformação , vamos derivar o perfil de velocidade dado no enunciado:
Organizando a equação:
Como e são constantes, podemos derivar u em relação a y:
Organizando:
Substituindo e
Opa! Encontramos a taxa de deformação!
Passo 3
Para achar a tensão cisalhante, vamos substituir a expressão que encontramos para a taxa de deformação na Lei de Newton da Viscosidade:
Substituindo:
Lembrando que a viscosidade da água é
Expressão para tensão cisalhante encontrada!
Passo 4
Agora, precisamos encontrar a tensão cisalhante na placa inferior, que é onde o enunciado quer saber a força, lembra?
Para isso, precisamos saber qual é o
A figura desse exercício é a mesma do anterior. Só que agora, queremos achar a tensão na placa de baixo.

Substituindo
Opa! Agora estamos quase lá. Lembra que esse exercício pediu a força e não a tensão. Então, vamos para o próximo passo!
Passo 5
Aprendemos na teoria que uma tensão é a razão entre força e área, certo?
Então, isolando a força:
E enunciado pede o valor da força numa seção de área igual a 1m² da placa inferior. Ou seja,
Então:
Substituindo:
Opa, encontramos a força! E qual é seu sentido? Como o resultado deu positivo e definimos na figura positivo sendo da esquerda para a direita. Então o sentido da Força é da esquerda para a direita.
Resposta
Sentido: da esquerda para a direita
Exercício Resolvido #6
Fox, McDonald, Pritchard, Introdução à Mecânica dos Fluidos, 8ª ed.Gen LTC, 2014, pp. 78, ex. 2.56
(Adaptada) Entre duas placas paralelas de área cada, estão contidos dois fluidos imiscíveis com viscosidades e conforme mostra a figura. As espessuras das camadas de líquido são e , respectivamente. a) Determine a força para fazer com que a placa superior se mova a uma velocidade de . b) Qual é a velocidade do fluido na interface entre os dois fluidos?
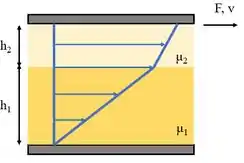
Passo 1
Fala aí, jovem padawan! Ansioso para lição Jedi de hoje? Vamos aprender a usar a famosa Tensão Cisalhante.
“Ué, mas o enunciado não tá pedindo a Força? Que mané Tensão Cisalhante!”
Olha, como se trata de fluidos, a tensão cisalhante é o caminho para achar a força. Lembra que a tensão é a força sobre a área? Então...
Como o enunciado está pedindo a força para fazer com que a placa se mova, então já conhecemos a área! É a área da placa, cujo valor é . Para achar a força, falta encontrar a tensão cisalhante. É justamente ela que vamos buscar agora.
Passo 2
Para fluidos newtonianos, sabemos que essa fórmula aqui é válida (e se chama Lei de Newton da Viscosidade).
A viscosidade de cada fluido foi dada pelo enunciado. Já temos esses valores. Show!
Agora vou te mostrar como calcular esse . A boa notícia é que não é cabuloso (ufa!). Na figura podemos ver que os perfis de velocidade de cada fluido são retas (estão em azul). Repare que são duas retas diferentes, uma para cada fluido. As velocidades nas placas e na interface estão destacadas na figura. é a velocidade na interface.
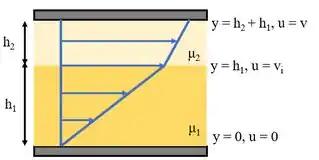
Então para achar esse de cada fluido, vamos fazer assim:
Como o enunciado diz os valores das alturas e , só vamos nos preocupar em colocar no sistema internacional. Logo: e . Além disso, queremos que a velocidade da placa superior seja , isto é, . Com isso, só falta descobrir para encontrar .
Passo 3
Aí que surge a sacada do exercício! A tensão do fluido 1 possui o mesmo valor em módulo da tensão do fluido 2 na interface. Ou seja, vamos igualar:
Substituindo e e as expressões que encontramos no Passo 2:
Lembrando que e e :
Reorganizando:
Encontramos a velocidade dos fluidos na interface!
Passo 4
E a força, jovem padawan?

Agora que sabemos quem é , nós vamos conseguir calcular . E, com isso, achamos a tensão cisalhante e, logo, a força!
Então, vamos lá, lembrando a equação que achamos:
A tensão cisalhante vai ser então:
Agora sim, podemos calcular a força
Resposta
Exercício Resolvido #7
Para o campo de tensão bidimensional da figura abaixo sabe-se que:
Encontre as tensões de cisalhamento e normal que atuam sobre o plano de corte AA no elemento, a um ângulo de como mostra a figura.
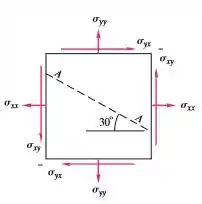
Passo 1
Queremos as tensões que irão atuar no elemento no plano de corte , então a primeira coisa que vamos fazer é desenhar o elemento cortado.
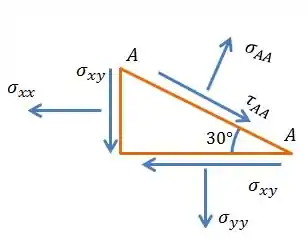
Para que o elemento não saia andando perdido pelo mundo o somatório de tensões deve ser zero, certo?
Bem, podemos fazer isso de duas formas, uma seria decompor as forças na direção do corte e a outra seria decompor as tensões na direção .
O mais fácil é decompor no plano do corte, assim podemos começar a fazer o sistema de equações para resolver o problema.
Passo 2
Então agora vamos fazer o sistema de equações na direção perpendicular ao corte . O somatório de forças nessa direção tem que ser zero, e nessa direção temos a ação da força normal e das outras tensões decompostas.
Então vamos começar a decompor as tensões, assumindo que está na direção positiva.
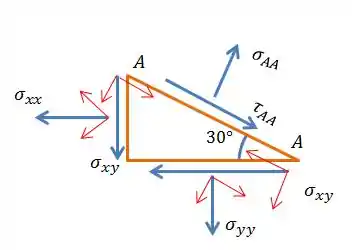
Só que a lei de Newton é sobre força e não pressão, então temos que multiplicar pelo comprimento do quadrado. O certo seria pela área, mas como a espessura é a mesma então cortamos ela e sobra só o comprimento, falou?
Confuso? Bem, olha a imagem abaixo, onde adotamos que o comprimento do corte é , assim o comprimento da lateral será e da base será .
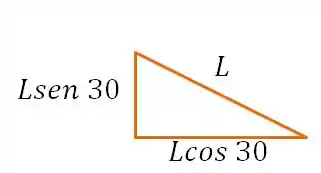
Multiplicando a tensão pelo comprimento do lado em que ela é aplicada temos:
Cortando e substituindo os valores dados no enunciado para descobrir temos:
Assim, o valor da tensão normal é:
Passo 3
Agora vamos equacionar na direção de cisalhamento:
Cortando o e substituindo os valores dados no enunciado para descobrir temos:
Resposta
Exercício Resolvido #8
Para o campo de tensão bidimensional da Figura abaixo considere que
Calcule:
a tensão de cisalhamento
a tensão de cisalhamento no plano .
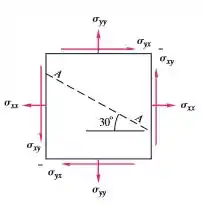
Passo 1
Como vimos na questão anterior, quando fazemos o corte temos a seguinte configuração:
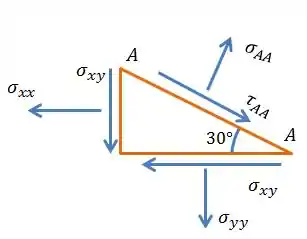
O equacionamento será feito igualzinho fizemos no exercício anterior, decompondo as tensões na direção do corte.
Repara que igualamos , porque o elemento não está sujeito à rotação.
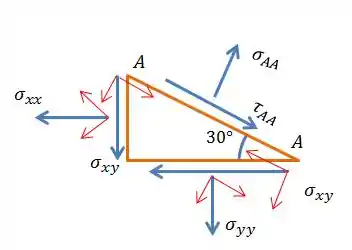
E na hora de equacionar, temos que lembrar que a lei de Newton é “somatório de forças igual a zero”, e o que temos é tensão. Pra transformar a nossa tensão em força, devemos multiplicá-la por uma área. Então consideramos a “profundidade” do elemento constante e multiplicamos as tensões pelo comprimento da “aresta” no qual cada tensão está atuando. Vamos definir o comprimento do corte como , então:
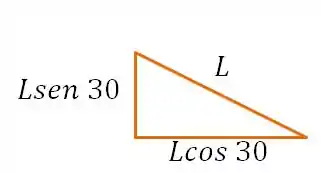
Agora vamos por todas as pressões na direção normal ao corte, multiplicando elas pelo comprimento do respectivo lado, beleza?
E assim vamos obter a seguinte equação:
Isso, nada mudou até agora em relação ao exercício anterior. O que vai mudar vai ser agora: não temos mais o valor de , mas temos o valor de .
Assim, cortando e substituindo os valores que temos, chegamos em:
Repare que todas as unidades são múltiplas de 1000. Então podemos escrever todas elas divididas por 1000 e vamos encontrar o resultado em .
Podemos isolar :
E resolvendo a equação, encontramos o valor de :
Passo 2
Bem, agora que temos a tensão , podemos igual fizemos na questão anterior resolver o problema.
Basta equacionarmos todas as pressões que atuam na direção de cisalhamento .
Cortando o e substituindo os valores dado no enunciado para descobrir temos: