Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 35

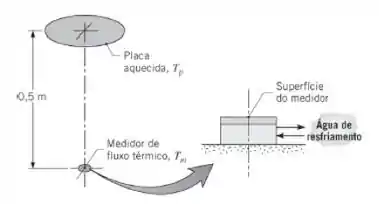
A configuração mostrada é usada para calibrar um medidor de fluxo térmico. O medidor tem uma superfície negra com 10 mm de diâmetro, que é mantida a 17°C por uma placa de suporte resfriada com água. O aquecedor, com 200 mm de diâmetro, tem uma superfície negra que é

mantida a 800 K e localizada a 0,5 m do medidor. A vizinhança e o ar estão a 27°C, e o coeficiente de transferência de calor por convecção entre o medidor e o ar é de 15 W m 2 K .

  1. Determine a troca de radiação líquida entre o aquecedor e o medidor.
  2. Determine a transferência de radiação líquida para o medidor por unidade de área do medidor.
  3. Qual é a taxa de transferência de calor líquida para o medidor por unidade de área do medidor?
  4. Se o medidor for construído de acordo com a descrição do Problema 3.107, que fluxo térmico ele indicará?

Passo 1

Vamos que vamos galerinha ?!

Bom, na letra (a) nós queremos achar a troca de radiação líquida entre o aquecedor e o medidor não é?

A fórmula vocês já sabem de cor, não é?

q a m = A a F a m σ T a 4 - T m 4 = A m F m a σ T a 4 - T m 4

Vamos ver o que temos?

σ = 5,67 × 10 - 8 W m 2 K 4

T a = 8 00   K

T m = 17 ° C + 273 = 290   K

A m = π D m 2 4 = π 0,01 2 4

A a = π D a 2 4 = π 0,2 2 4

L = 0,5   m

Bom, nós ainda não temos os fatores de forma, não é?

Mas nós temos uma fórmula para estas situações, ok?

F m a = D a 2 4 L 2 + D a 2

Substituindo:

F m a = 0,2 2 4 0,5 2 + 0,2 2 = 0,0385

Nós temos todos os dados que precisamos, então vamos substituir na igualdade:

q a m = π 0,01 2 4 . 0,0385 5,67 × 10 - 8 800 4 - 290 4

q a m = 69 × 10 - 3 W

Passo 2

Agora, a letra (b) nos pediu para achar a transferência de radiação líquida para o medidor por unidade de área do medidor.

Como o medidor recebe radiação do aquecedor e da vizinhança:

q " r a d ,   m e d i d o r = q a m A m + q v i z ,   m A m

Já sabemos q a m e A m , certo? Então só precisamos achar q v i z ,   m ! Se lembram da fórmula?

q v i z ,   m = A m F m , v i z σ T v i z 4 - T m 4

Então:

q " r a d ,   m e d i d o r = q a m A m + F m , v i z σ T v i z 4 - T m 4

Usando o somatório para a superfície do medidor:

F m , v i z + F m a = 1     ∴     F m , v i z = 1 - F m a

Substituindo:

q " r a d ,   m e d i d o r = q a m A m + σ 1 - F m a T v i z 4 - T m 4

Substituindo tudo:

q " r a d ,   m e d i d o r = 69 × 10 - 3 π 0,01 2 4 + 5,67 × 10 - 8 1 - 0,0385 300 4 - 290 4

q " r a d ,   m e d i d o r = 934,5 W m 2

Passo 3

Shoow de boola, agora vamos seguindo para a letra (c) !!

Para a letra (c) nós queremos achar a transferência de calor líquida para o medidor por unidade de área do medidor, então aqui nós temos que considerar não só a radiação, mas também a convecção !!

q " t o t a l ,   m e d i d o r = q " r a d ,   m e d i d o r + q " c o n v ,   m e d i d o r

Nós também já sabemos como se calcula o calor convectivo:

q " c o n v ,   m e d i d o r = h T v i z - T m

Então:

q " t o t a l ,   m e d i d o r = q " r a d ,   m e d i d o r + h T v i z - T m

O calor convectivo o problema já nos deu:

h = 15 W m 2 K

Substituindo:

q " t o t a l ,   m e d i d o r = 934,5 + 15 300 - 290

q " t o t a l ,   m e d i d o r = 1085 W m 2

Passo 4

A letra (d) nos pede para avaliar se o medidor for construído de acordo com a descrição do Problema 3.107, que fluxo térmico ele indicará?

No problema 3.107 nós não temos calor convectivo, só o radiante !!

Calculando o fluxo de calor radiante por unidade de área do medidor:

q " m = A m F m a σ T a 4 A m = F m a σ T a 4

Substituindo:

q " m = 0,0385 5,67 × 10 - 8 800 4

q " m = 894 W m 2

Sucessooo galerinhaa, terminamos mais umaa !!

Resposta

  1. q a m = 69 × 10 - 3 W
  2. q " m e d i d o r = 934,5 W m 2
  3. q " t o t a l ,   m e d i d o r = 1085 W m 2
  4. q " m = 894 W m 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fluido criogênico escoa por um tubo com 20 mm de diâmetro, cuja superfície externa é difusa e cinza, com uma emissividade de 0,02 e uma temperatura de 77 K. Esse tubo é concêntrico a um tubo maior,
13.55 Duas esferas concêntricas com diâmetro D1 = 0,8 m e D2 = 1,2 m estão separadas por um espaço contendo ar e têm temperaturas superficiais de T1 = 400 K e T2 = 300 K.Se as superfícies forem negras
Um aquecedor radiante é constituído por um banco de tubos cerâmicos com elementos aquecedores internos. Os tubos têm diâmetro D = 20 mm e estão separados por uma distância s = 50 mm. Uma superfície re
Revestimentos aplicados a longas tiras metálicas são curados pela instalação das tiras ao longo das paredes de um longo forno com seção transversal quadrada.As condições térmicas no interior do forno
O revestimento sobre uma superfície metálica com dimensões de 1 m por 2m é curado pela sua colocação sob uma superfície eletricamente aquecida de dimensões equivalentes, a uma distância de 0,5 m. O co