Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 56

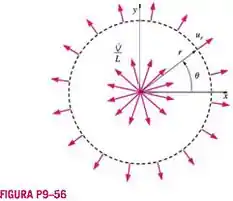
Considere o escoamento bidimensional permanente, incompressível devido a uma linha de fontes na origem (Figura P9-56). O fluido é criado na origem e se espalha rapidamente em todas as direções no plano x y . A vazão total em volume do fluido criado por unidade de largura é V ˙ / L (para dentro da página da Figura P9-56), onde L é a largura da linha de fontes entrando na página na Figura P9-56. Como a massa deve ser conservada em todos os pontos exceto na origem (um ponto de singularidade), a vazão em volume por unidade de largura através de um círculo de raio r qualquer também deve ser V ˙ / L . Se especificarmos (arbitrariamente) que a função corrente ψ seja zero ao longo do eixo x positivo θ = 0 , qual será o valor de ψ ao longo do eixo y positivo θ = 90 ° ? Qual é o valor de ψ ao longo do eixo x negativo θ = 180 ° ?

Passo 1

O problema quer saber quanto vale a função corrente ψ y + ao longo do eixo y positivo e quanto vale a função corrente ψ x - ao longo do eixo x negativo. Para calcular esses dois valores, temos que nos lembrar da equação 9-25 do livro. Ela diz que a vazão por unidade de largura V ˙ 12 L que passa entre duas linhas de correntes ψ 1 e ψ 2 , deve ser igual a ψ 2 - ψ 1 .

V ˙ 12 L = ψ 2 - ψ 1

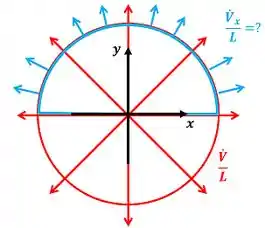
A figura abaixo mostra as linhas de corrente e a vazão por unidade de largura da nossa questão.

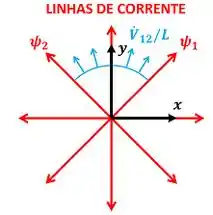
Agora nós temos que aprender a usar essa equação para calcular o que queremos.

Passo 2

Para calcular o valor da função corrente ψ y + ao longo do lado positivo do eixo y , podemos usar a equação para o escoamento entre duas linhas de corrente: a linha de corrente que está sobre o eixo x positivo (que tem o valor de função corrente igual a ψ x + = 0 segundo o enunciado) e a linha de corrente que está sobre o eixo y positivo (que tem o valor de função corrente igual a ψ y + ). Essas duas linhas de corrente estão representadas na figura abaixo.

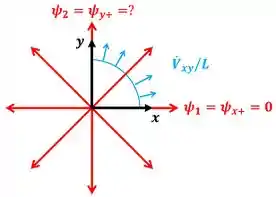
onde V ˙ x y / L é a vazão volumétrica por unidade de largura do escoamento entre as linhas de corrente sobre o eixo x positivo e sobre o eixo y positivo.

Substituindo ψ 2 por ψ y + , ψ 1 por ψ x + e V ˙ x y L por V ˙ 12 L , achamos:

V ˙ 12 L = ψ 2 - ψ 1     ⟹     V ˙ x y L = ψ y + - ψ x +     ⟹     V ˙ x y L = ψ y + - 0     ⟹     ψ y + = V ˙ x y L

A equação acima mostra que para achar ψ y + , precisamos encontrar V ˙ x y L .

Passo 3

V ˙ x y L pode ser calculado usando regra de três e lembrando que V ˙ L é a vazão por unidade de largura que atravessa todo o perímetro do círculo. Como V ˙ x y L é a vazão por unidade de largura que passa por 1 / 4 do perímetro do círculo, podemos formular a seguinte pergunta: se a vazão por unidade de largura que atravessa todo o perímetro do círculo vale V ˙ L , quanto vale a vazão por unidade de largura V ˙ x y L que atravessa 1 / 4 do perímetro do círculo?

A vazão por unidade de largura V ˙ x y L de 1 / 4 do perímetro total do círculo vale 1 / 4 da vazão total por unidade de largura V ˙ L .

V ˙ x y L = 1 4 V ˙ L

Substituindo isso na equação de ψ y + , achamamos:

ψ y + = V ˙ x y L       ⟹       ψ y + = 1 4 V ˙ L

Passo 4

Podemos repetir o mesmo processo para calcular o valor da função corrente ψ x - da linha de corrente que está sobre o eixo x negativo. Só que agora, vamos usar a equação para o escoamento entre outras duas linhas de corrente: a linha de corrente que está sobre o eixo x positivo (que tem o valor de função corrente igual a ψ x + = 0 segundo o enunciado) e a linha de corrente que está sobre o eixo x negativo (que tem o valor de função corrente igual a ψ x - ). Essas duas linhas de corrente estão representadas na figura abaixo.

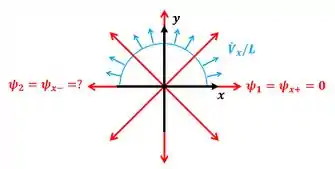
onde V ˙ x / L é a vazão volumétrica por unidade de largura do escoamento entre as linhas de corrente sobre o eixo x positivo e sobre o eixo x negativo.

Substituindo ψ 2 por ψ x - , ψ 1 por ψ x + e V ˙ x L por V ˙ 12 L , achamos:

V ˙ 12 L = ψ 2 - ψ 1     ⟹     V ˙ x L = ψ x - - ψ x +     ⟹     V ˙ x L = ψ x - - 0     ⟹     ψ x - = V ˙ x L

A equação acima mostra que para achar ψ x - , precisamos encontrar V ˙ x L .

Passo 5

V ˙ x L também pode ser calculado usando regra de três e lembrando que V ˙ L é a vazão por unidade de largura que atravessa todo o perímetro do círculo. Como V ˙ x L é a vazão por unidade de largura que passa por 1 / 2 do perímetro do círculo, podemos formular a seguinte pergunta: se a vazão por unidade de largura que atravessa todo o perímetro do círculo vale V ˙ L , quanto vale a vazão por unidade de largura V ˙ x L que atravessa 1 / 2 do perímetro do círculo?

A vazão por unidade de largura V ˙ x L de 1 / 2 do perímetro total do círculo vale 1 / 2 da vazão total por unidade de largura V ˙ L .

V ˙ x y L = 1 2 V ˙ L

Substituindo isso na equação de ψ x - , achamamos:

ψ x - = V ˙ x L       ⟹       ψ x - = 1 2 V ˙ L

Resposta

a   ψ y + = 1 4 V ˙ L

b   ψ x - = 1 2 V ˙ L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Neste capítulo mencionamos rapidamente a função corrente compressível ψ p , definida em coordenadas cartesianas ρ u = ∂ ψ p / ∂ y e ρ v = - ∂ ψ p / ∂ x . Quais são as dimensões primárias de ψ p ? Escr
No Exemplo 9-2 nós fornecemos expressões para u , v e ρ para escoamento através de um duto compressível convergente.Encontre uma expressão para a função corrente compressível ψ p que descreve esse cam
No Problema 9-20 desenvolvemos expressões para u , v e ρ para escoamento através de um túnel de vento de alta velocidade. Encontre uma expressão para a função corrente compressível ψ p que descreva es
A equação geral do volume de controle para a conservação do momento linear é: ∫ V C ρ g → d V + ∫ S C σ i j ∙ n →d A = ∫ V C ∂ ∂ t ρ V → d V + ∫ S C ρ V → V → ∙ n →d A Discuta o significado de cada te
A média no tempo de um escoamento bidimensional turbulento, incompressível, sobre um bloco quadrado de dimensão h = 1 m é modelado com um aplicativo comercial de dinâmica dos fluido computacional (CFD