Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 67
Uma parede plana composta e unidimensional tem espessura global igual a . O Material está no domínio e há no seu interior uma reação química exotérmica que ocasiona uma taxa de geração volumétrica uniforme . O Material está no domínio e há no seu interior uma reação química endotérmica que ocasiona uma taxa de geração volumétrica uniforme . As superfícies em estão isoladas termicamente. Esboce as distribuições, em regime estacionário, de temperaturas e de fluxos térmicos, e , respectivamente, no domínio para , e . Aponte as características importantes das distribuições que você desenhou. Se , você pode esboçar a distribuição de temperaturas no regime estacionário?
Passo 1
Vamos lá! primeiro vamos entender nosso problema, o problema diz que se trata de dois materiais em contato um com o outro mas isolados termicamente do meio, um sofre um processo exotérmico (libera calor) e o outro passa por um processo endotérmico (absorve calor), pra deixar isso mais claro vamos analisar um esquema gráfico do nosso sistema
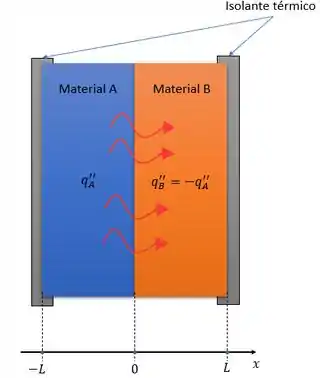
Origem e sentido da geração de calor e da dissipação.
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
Tendo tudo isso em mente vamos escrever nossa lei de Fourier pra podermos analisar a dinâmica do problema.
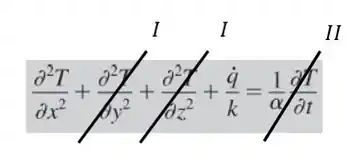
Como nossa condução é unidimensional e há geração de energia, temos:
Esse resultado nos indica que o fluxo de calor varia linearmente com , pois se integrarmos ambos os lados da equação temos:
Aplicando nossas condições de contorno, temos:
Lembrando que o fluxo pode ser dependendo do lado que estamos, o que garante nossa condição de contorno para todo o material.
Com esses dados em mãos vamos montar nosso gráfico, assim temos:
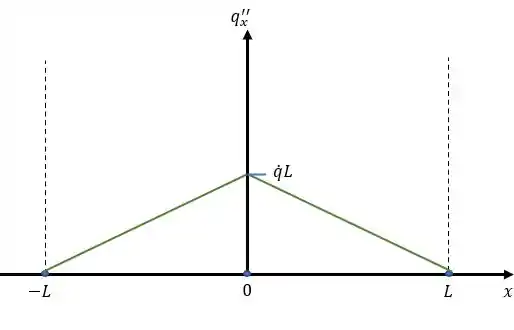
Passo 3
(b) Vamos refazer o passo anterior agora com o foco em encontrar
Integrando duas vezes temos:
Usando nossas condições de contorno temos:
Como não temos dados o suficiente para inferir uma condição de contorno para encontrarmos , vamos manter ela assim na equação, assim vamos montar nosso gráfico para
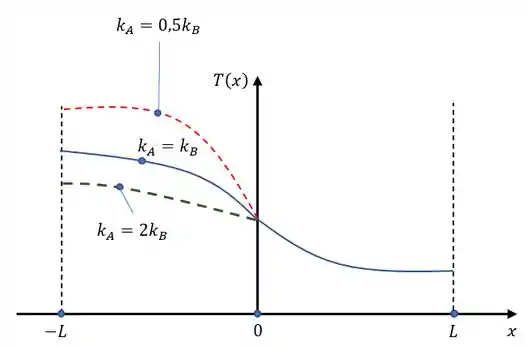
Nossa é uma equação do segundo grau, mas como o fator que o multiplica muda de sinal de acordo com o material temos uma mudança no sentido da concavidade da parábola.
Como é inversamente proporcional a nossa temperatura, da forma que mostramos na nossa equação, quanto menor for o maior será a nossa temperatura. (no caso maior será o pico da concavidade da nossa parábola.
Passo 4
Pra terminarmos de vez com nosso problema vamos fazer o balanço de energia assim.
Para temos:
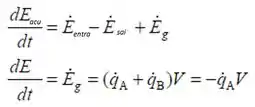
Como é o volume e a variação de energia acumulada é diferente de , logo nosso sistema não pode atingir o estado permanente tendo em vista que ele está acumulando energia constantemente enquanto os processos estão ocorrendo.
Isso é tudo pessoal! \o/
Resposta
Ei, a resposta está no passo a passo :)