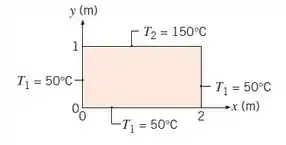
Uma placa retangular bidimensional está sujeita às condições de contorno prescritas. Usando os resultados da solução exata para a equação do calor apresentada na Seção 4.2, calcule as temperaturas ao longo do plano médio da placa () em , e considerando os primeiros cinco termos diferentes de zero da série infinita. Avalie o erro resultante do uso apenas dos três primeiros termos da série infinita.

Da Seção 4.2, a distribuição da temperatura é

Considerando agora o ponto e, portanto, , e , temos o seguinte:

Podemos perceber que quando é um numero par , o termo

Logo, os primeiro 5 termos não nulos serão quando . Substituindo, temos:

Portanto a temperatura em é .

Considerando agora o ponto e, portanto, , e , temos o seguinte:

Podemos perceber que quando é um numero par , o termo

Logo, os primeiro 5 termos não nulos serão quando . Substituindo, temos:

Portanto a temperatura em é .

Considerando agora o ponto e, portanto, , e , temos o seguinte:

Podemos perceber que quando é um numero par , o termo

Logo, os primeiro 5 termos não nulos serão quando . Substituindo, temos:

Portanto a temperatura em é .

Usando uma HP, se usarmos apenas os 3 primeiros termos do somatório, vamos encontrar as seguintes temperaturas:

Considerando agora o ponto

Considerando agora o ponto

Considerando agora o ponto

Podemos perceber que utilizando apenas 3 termos não nulos vamos encontrar valores muito próximos.