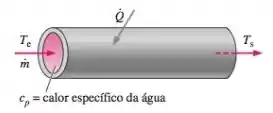
A taxa de transferência de calor para a água que escoa em um tubo foi analisada no Problema 7-20. Vamos abordar esse mesmo problema, mas agora com a análise dimensional. A água fria entra em um tubo, onde ela é aquecida por uma fonte externa de calor (Figura P7-64). As temperaturas de entrada e saída da água são e , respectivamente. Sabe-se que a taxa total de transferência de calor da vizinhança para a água do tubo é uma função da vazão de massa , do calor específico da água e da diferença de temperatura entre a água de entrada e de saída. Mostrando todo o seu trabalho, use a análise dimensional para encontrar a relação funcional entre esses parâmetros e a compare com a equação analítica dada no Problema 7-20. (Observação: estamos considerando que não conhecemos a equação analítica.)

Como temos quatro dimensões primárias, é esperado que . Assim, número de grupos esperados são:

Isso não está correto e, com isso, vamos reduzir em um:

Logo:

Assim teremos 1 número adimensional .

Vamos agora escolher três parâmetros que se repetem. Como a taxa de transferência de calor é escrita em função de três termos, escolhemos esses mesmos como parâmetros repetitivos. Assim:

Vamos obter os expoentes a, b e c comparando os expoentes de cada dimensão primária do lado esquerdo com o lado direito da relação do número

Massa:

Comprimento:

Temperatura:

A dimensão relacionada ao tempo pode ser usada para conferir que os expoentes estão corretos.

Substituindo os expoentes na relação do número adimensional temos:

Como temos somente 1 número , podemos considerá-lo como uma constante. Temos assim:

Essa relação obtida utilizando análise dimensional difere-se da equação analítica, dada por , onde temos que . No caso da análise dimensional, para que se tenha um valor para , é preciso realizar experimentos para determinar o valor da constante.