Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 45
Um tubo de 12 cm de diâmetro, contendo água escoamento a 200 N/s, sofre uma restrição por uma placa de orifício, como mostra a figura abaixo. O jato de saída tem 25 mm de diâmetro. A pressão no tubo na seção 1 é de 800 kPa (manométrica). Calcule a força F necessária para manter presa a placa de orifício.
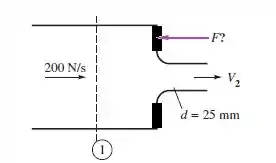
Passo 1
E aí galera, bora pra mais uma aventura de mecflu?
Vamos de início escrever nosso balanço de forças, beleza? E pra isso vamos definir nosso volume de controle como sendo mostrado abaixo:
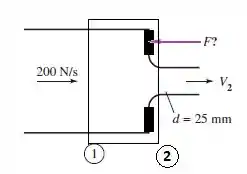
O balanço de forças vai mostrar pra gente que temos uma força de pressão contrapondo a força F e as forças causadas pelo escoamento também, certo? Então vamos escrever isso!!! Outra coisa importante é que se você adicionar a pressão atmosférica em todos os pontos (figura abaixo), perceberá que a pressão no ponto 2 deve ser igual a pressão atmosférica, então a pressão no ponto 1 deve ser ela menos a pressão atmosférica, ou seja, a própria pressão manométrica.
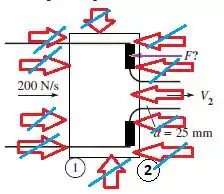
Passo 2
A vazão mássica deve ser dada pela equação abaixo e para um escoamento incompressível, sabemos que a vazão de entrada é igual a vazão de saída.
Vamos converter para vazão volumétrica, beleza?
Olha que show, agora que sabemos qual é a vazão volumétrica conseguimos determinar qual é a velocidade em cada um dos pontos.
Onde
Sabemos que e