Intensidade de Radiação
Teoria
Introdução
Vamos começar olhando para um objeto que está emitindo radiação, beleza?
Essas setinhas nos indicam o caminho que a radiação está fazendo… Mas então quer dizer que a radiação não é uniforme e atua em diferentes direções? Exatamente!!
A radiação emitida por uma superfície plana para o hemisfério acima dela depende da direção da radiação em relação a essa superfície.
Sendo assim, vamos precisar de algo que descreva a magnitude da radiação, seja emitida ou incidente sobre uma superfície, em uma determinada direção do espaço. A grandeza que irá descrever essa magnitude é justamente intensidade de radiação .
Sabe quando a gente tá com um espelhinho na mão e a luz reflete no espelhinho e aparece uma claridade em um lugar diferente dependendo do ângulo que o espelho está? É mais ou menos esse o espírito da coisa!!
Vamos dar uma olhada nesse esquema:
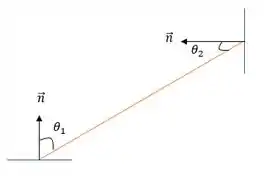
Imagina que temos dois espelhos, um na nossa mão e outro na parede e dependendo de como eu posiciono o espelho que está na minha mão eu vou ter e diferentes!
Agora vamos pegar um exemplo de radiação!! Vamos considerar uma pequena superfície com área , que emite difusamente com um poder emissivo hemisférico total de , essa superfície é representada pela estrela.
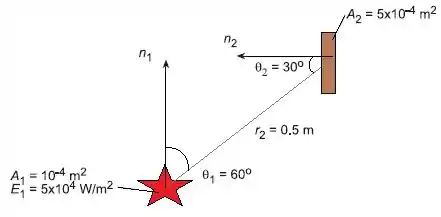
Em um mundo ideal, se todas as superfícies no mundo emitissem radiação da mesma forma em todas as direções, a potência emissiva resolveria sem muitos problemas a nossa vida, mas não é bem isso que acontece na vida real.
O que queremos saber aqui é: a que taxa essa emissão é interceptada por uma superfície com área , representada por um retângulo na figura acima?
Além disso, qual é a irradiação sobre ?
Olha só, nesse problema a gente tem a normal , fazendo um ângulo na superfície emissiva em relação a radiação que está sendo emitida, e a normal , fazendo um ângulo na superfície interceptada pela emissão… Além disso, o exemplo diz pra gente que a distância de uma superfície para a outra é de , beleza?
Bom, mas antes de qualquer coisa, vamos precisar arranjar uma forma de quantificar adequadamente a direção com que essa radiação está sendo emitida.
Ângulo Sólido
Para que a nossa vida fique mais tranquila, a melhor forma de especificar a direção com que a radiação está sendo emitida é utilizando coordenadas esféricas. Assim, a ideia é basicamente essa:
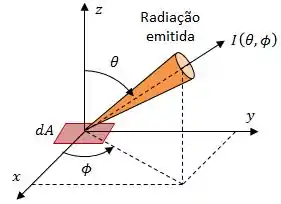
Tá lembrado de coordenadas esféricas? Observando a figura, vemos quais as coordenadas que trabalhamos nesse caso! Temos o ângulo de zênite, que varia , o ângulo de azimute, que varia e teremos a terceira coordenada que será dada pelo raio que será a distância até o centro.
Porém, só essas não são suficientes pra gente resolver os problemas de intensidade de radiação… É que estamos trabalhando com duas áreas diferentes, então precisamos que alguma ajuda que indique uma relação entre essas áreas… Adivinha só quem vai fazer esse papel?
O ângulo sólido! Ele é composto pelos ângulos (ângulo de zênite) e (ângulo de azimute) que usamos para as coordenadas esféricas!
O ângulo sólido é definido da seguinte forma:
A unidade do ângulo sólido e o “steradian” ou esfera radiano.
Pra entender melhor, vamos fazer uma comparação com o ângulo plano que estamos mais acostumados!! Se temos um ângulo a gente pode associar ele a um comprimento de arco (), certo?
Podemos dizer então que:
Então, assim como o ângulo plano está associado ao comprimento de um arco, o ângulo sólido está associado a uma área superficial sobre a qual a radiação está incidindo, beleza? Dessa forma aqui:
Bom, mas e se essa área não for exatamente perpendicular à direção radial do nosso sistema de coordenadas, fazendo um ângulo com o mesmo… Bom, aí podemos escrever que:
Voltando agora ao nosso problema, a direção normal da área está fazendo um ângulo de com a direção de emissão da radiação. Tanto como são muito pequenas em relação a entre elas, por isso podemos tratá-las como infinitesimal. Portanto vamos assumir que , que é a área que está recebendo a radiação.
Assim, o ângulo sólido será dado por:
E substituindo nossas informações:
“Beleza, mas como esse ângulo está associado com a taxa de energia de radiação que a área emite sobre a área ?”
Muito boa a pergunta!
Intensidade de Radiação
A intensidade de radiação para a radiação emitida é definida como a taxa de energia emitida por unidade de área e unidade de ângulo sólido, nesta direção:
Como não temos o valor da intensidade de radiação nem da taxa de troca de energia é necessário encontrar a intensidade de radiação a partir do poder emissivo, beleza?
O fluxo de radiação para a radiação emitida é a potência emissiva . Se observarmos o hemisfério acima da superfície plana que está emitindo radiação, essa potência emitida pode ser calculada da seguinte forma:
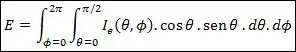
“Então vou ter sempre que calcular essa integral?”
Bom, no caso de uma superfície que tenha uma emissão difusa (como é o nosso caso), a intensidade de radiação é constante (saindo da integral), não dependendo da direção. Nesse caso, a potência emissiva será dada por:
Voltando ao nosso problema, como o mesmo já nos deu a potência emissiva, podemos calcular a intensidade da radiação emitida pela área , que será dada por:
Se usarmos a definição de intensidade de radiação, podemos calcular a taxa de energia passada da superfície 1 para superfície 2 da seguinte forma:
Substituindo os valores:
Ainda temos que falar sobre a Irradiação
Irradiação é como definimos o fluxo de radiação incidente sobre uma superfície de todas as direções.
Vamos definir a irradiação de uma forma muito semelhante a como fizemos anteriormente com o poder emissivo, a diferença é que agora vamos usar a intensidade de radiação incidente .
Dessa forma, temos que:
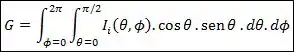
Assim, como antes, se a radiação incide na superfície difusa, podemos dizer que:
Vamos lembrar que o nosso exemplo também pediu a irradiação na superfície 2, ok? Nesse caso, as coisas vão ser mais tranquilas porque, como já calculamos a taxa de energia trocada entre as superfícies , a irradiação será dada por:
Radiosidade
Quando a radiação incide sobre uma superfície, parte dela é refletida. Dessa forma, a radiação total que deixa uma superfície é a soma das radiações emitida e refletida pela mesma… Dá uma olhadinha nesse esquema que dá pra visualizar melhor:
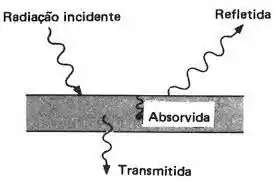
Temos uma superfície que está absorvendo e refletindo radiação ao mesmo tempo… E se a gente quantificar apenas uma energia de radiação deixando a superfície, ao invés de separar esses dois? Chegaremos assim na radiosidade , que é a taxa de energia que deixa uma unidade de área em todas as direções.
Podemos expressá-la da seguinte forma:
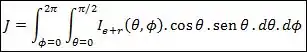
Onde é a soma das intensidades de radiação emitida e refletida. Dessa forma, se novamente tivermos uma superfície difusa que seja uma emissora e uma refletora, a radiosidade será dada por:
Agora já podemos partir pros exercícios!
Ângulo Sólido ω
Intensidade de Radiação I e
Ainda temos que falar sobre a Irradiação G
Radiosidade J
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Uma pequena superfície estacionária de área emite difusamente com uma intensidade total de .
Uma segunda superfície de área equivalente está localizada a uma distância fixa de de . A linha de conexão entre as duas superfícies permanece perpendicular a , enquanto gira a uma frequência angular .
Qual é a quantidade de energia interceptada pelos dois lados de durante uma volta completa?
Passo 1
A taxa de energia emitida por e interceptada por é dada por:
Como as dimensões das placas são muito menores do que a distância entre elas, podemos tratar o ângulo sólido da seguinte forma:
Assim, a taxa de transferência de calor será dada por:
Além disso, como a linha que liga as duas placas é perpendicular à placa , . Logo:
Passo 2
O problema nos pediu pra calcular a energia interceptada pela placa em uma volta completa.
A taxa de energia de radiação que calculamos no Passo 1 pode ser escrita como:
Substituindo a expressão que encontramos no Passo 1:
Nessa expressão, somente varia com o tempo, onde a velocidade angular é dada por:
Na hora de definir os limites de integração, temos que ter muito cuidado aqui!
Em uma volta completa, o ângulo entre a linha que liga as duas placas e a linha normal à placa 2 irá variar de a quatro vezes. Sendo assim, podemos fazer os limites integração e multiplicar a expressão inteira por 4.
Extamos fazendo isso porque, se fizermos o ângulo variando entre e , a integral será igual a zero, e serio o mesmo que dizer que nenhuma energia interceptou a placa 2, o que estaria errado.
Sendo assim:
Passo 3
Fazendo a integral:
Substituindo os valores:
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Uma fornalha com uma abertura de de diâmetro e poder emissivo de é usada para calibrar um medidor de fluxo térmico que tem uma área sensora de .
A qual distância, medida ao longo da normal a partir da abertura, o sensor deve ser posicionado para receber uma irradiação de ?
Se o sensor for inclinado para fora da normal em , qual será a sua irradiação?
Passo 1
A qual distância, medida ao longo da normal a partir da abertura, o sensor deve ser posicionado para receber uma irradiação de ?
Vamos primeiro entender o problema: repara que o sensor está posicionado de frente pra abertura da fornalha. Então a “linha” que une essas duas superfícies passa exatamente pela normal deles, de modo que .
Aí em cima indicamos também a , calculada a partir do diâmetro dado, a dada e o dado.
E a gente quer saber qual deve ser a distância entre a abertura da fornalha e o sensor para que a irradiação recebida pelo sensor seja igual a
Passo 2
Então vamos colocar isso em fórmulas.
A irradiação entre a fornalha e o sensor pode ser escrita como:
Onde a taxa de calor que sai da fornalha e atinge o sensor é dada por:
Supondo que as áreas do sensor e a abertura na fornalha sejam muito menores que a distância entre elas, o ângulo sólido pode ser calculado da seguinte forma:
Além disso, considerando que a fornalha emite calor difusamente, a intensidade de radiação será dada por:
Assim, substituindo tudo isso na expressão da taxa de energia de radiação, teremos que:
Passo 3
Reorganizando os termos da equação que encontramos no passo anterior:
Onde a taxa de energia de radiação é dada por:
Dessa forma, a distância entre as placas será:
Onde:
Substituindo os valores:
Passo 4
Se o sensor for inclinado para fora da normal em , qual será a sua irradiação?
Agora a gente já sabe a distância entre as superfícies, então só precisa girar um pouquinho o sensor assim:
Nesse caso, a irradiação será dada por:
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Uma pequena fonte de radiação emite difusamente com uma intensidade . O detector de radiação está alinhado normal à fonte a uma distância de .
Uma tela opaca está posicionada na meta de do caminho entre e para impedir que a radiação da fonte atinja o detector. A pequena superfície é um espelho difuso perfeito que permite que a radiação emitida pela fonte seja refletida para o detector.
Calcule a potência radiante incidente em devido à emissão a partir da fonte , .
Supondo que a potência radiante, seja refletida perfeita e difusamente, calcule a intensidade deixando , .
Calcule a potência radiante incidente em devida à radiação refletida deixando , .
Passo 1
Calcule a potência radiante incidente em devido à emissão a partir da fonte , .
A potência radiante que sai de e atinge é dada por:
Supondo que as áreas e sejam muito menores que a distância entre elas, o ângulo sólido pode ser calculado da seguinte forma:
Onde e .
Voltando à expressão da potência radiante:
Substituindo os valores:
Passo 2
Supondo que a potência radiante, seja refletida perfeita e difusamente, calcule a intensidade deixando , .
Se a radiação for refletida difusa e perfeitamente, a intensidade de radiação que deixará será:
Passo 3
Calcule a potência radiante incidente em devida à radiação refletida deixando , .
A potência radiante pode ser escrita da seguinte forma:
Onde o ângulo sólido pode ser aproximado por:
Assim, a potência radiante será:
Substituindo os valores:
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
De acordo com a sua distribuição direcional, a radiação solar que incide sobre a superfície terrestre pode ser dividida em duas parcelas. A parcela direta, que é constituída por raios paralelos que incidem em um ângulo fixo , e a parcela difusa, formada por radiação que pode ser aproximada como sendo distribuída de forma difusa em relação a .
Considere condições de céu claro nas quais a radiação direta incide com um ângulo , com um fluxo total (baseado na área normal aos raios) de , e a intensidade total de radiação difusa é de .
Qual é o valor da irradiação solar total na superfície terrestre?
Passo 1
A irradiação total é dada pela somas das irradiações direta e difusa, logo:
A irradiação direta é dada por:
Enquanto a irradiação difusa é dada por:
Portanto:
Passo 2
Substituindo os valores:
Resposta
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Em um dia encoberto, a distribuição direcional da radiação solar que incide na superfície terrestre pode ser aproximada por uma expressão na forma , onde é a intensidade total da radiação normal à superfície e é o ângulo de zênite.
Qual é a irradiação solar na superfície terrestre?
Passo 1
Por definição, a irradiação é dada por:
Onde . Logo:
Como os termos da integral dependem somente de , podemos resolver a integral da seguinte forma:
Passo 2
A primeira integral será igual a .
Para resolver a segunda integral, vamos fazer uma integração por substituição, onde :
Logo:
Onde , logo:
Resposta
Exercício Resolvido #6
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
A distribuição espectral da radiação emitida por uma superfície difusa pode ser aproximada como segue.
Qual é o poder emissivo total?
Qual é a intensidade total da radiação emitida na direção normal e em um ângulo de em relação à normal?
Determine a fração do poder emissivo total deixando a superfície nas direções .
Passo 1
Qual é o poder emissivo total?
Como o problema está nos dando a distribuição em função de comprimentos de onda, o poder emissivo total será dado por:
Passo 2
Qual é a intensidade total da radiação emitida na direção normal?
Tratando a superfície como difusa, a intensidade de radiação será dada por:
Passo 3
Determine a fração do poder emissivo total deixando a superfície nas direções .
O que estamos querendo calcular aqui é:
Como a intensidade de radiação é constante:
As integrais podem ser separadas em:
Onde a primeira integral será igual a e a segunda integral pode ser resolvida por substituição, onde:
Dessa forma:
Resposta
Exercício Resolvido #7
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptado) Durante o tratamento térmico por radiação de um material na forma de uma fina película hemisférica é mantida por uma pressão de ar relativamente baixa. A irradiação sobre a película é devida à emissão de um aquecedor radiante com área , que emite de forma difusa com uma intensidade .
Obtenha uma expressão para a irradiação sobre a película como um função do ângulo de zênite .
Passo 1
A irradiação sobre a superfície infinitesimal está associada com a taxa de energia por radiação da seguinte forma:
Onde a taxa de energia por radiação é dada por:
Onde o ângulo sólido é dado por:
Finalmente, a irradiação será:
Resposta
Exercício Resolvido #8
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptado) Uma pequena fonte de calor radiante com área emite difusamente com uma intensidade . Uma segunda área pequena, está localizada como mostrado no esboço a seguir.
Determine a irradiação de para .
Passo 1
A irradiação de é dada por:
Onde a taxa de calor que sai da fornalha e atinge o sensor é dada por:
Como as áreas são muito menores que a distância entre elas, o ângulo sólido pode ser calculado da seguinte forma:
Dessa forma, a irradiação será dada por:
Passo 2
Onde:
Dessa forma, a irradiação será:
