Introdução à Radiação
Teoria
Introdução
Imagine que, de alguma forma, a gente consiga colocar um objeto quente no interior de uma superfície fria, mas entre o objeto e a superfície há apenas vácuo.
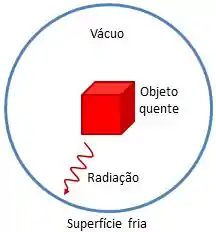
Querendo ou não o objeto irá se resfriar e a superfície irá se aquecer, isso vai ocorrer até que não haja diferença de temperatura entre os dois.
Bom, a transferência de calor entre esses dois carinhas não vai poder ocorrer nem por condução, e nem por convecção, já que não há um meio material entre esses dois caras. Essa transferência de calor vai ocorrer por radiação térmica.
A diferença da radiação para os outros dois mecanismos de transferência de calor é que a radiação não precisa de um meio material para ocorrer. Um exemplo disso é a energia do Sol que atinge a Terra, uma vez que existe vácuo entre os dois.
Justamente por se propagar no vácuo, a radiação térmica é definida com uma onda eletromagnética, mas com comprimentos de onda que variam entre e , aproximadamente.
Essa radiação térmica é emitida por todos os corpos que possuem temperatura acima do zero absoluto, ou seja, você, sua mesa, seu computador, as paredes da sua casa... todos eles emitem radiação térmica.
Pensando ainda no Sol, por exemplo, tratando-o como um corpo negro a uma temperatura efetiva de , qual é a taxa em que energia de radiação infravermelha é emitida pelo Sol?
Antes de qualquer coisa, a primeira pergunta que temos que responder é:
O que é um Corpo Negro?!
Um corpo negro é um corpo idealizado que possui as seguintes características:
- Um corpo negro absorve toda a radiação que incide sobre ele, independente do comprimento de onda e da direção;
- Um corpo negro emite radiação térmica uniformemente em todas as direções. Ou seja, o corpo negro é um emissor difuso;
- Para uma determinada temperatura e comprimento de onda, nenhuma superfície pode emitir mais energia do que um corpo negro.
A taxa de energia total emitida pelo corpo negro é dada por:
Onde é dado em , além disso:
: Temperatura absoluta da superfície ;
: Constante de Stefan-Boltzmann .
No nosso problema, como estamos considerando que o Sol tem uma temperatura de , teremos:
Embora o corpo negro seja algo idealizado, um tipo de corpo que é bem parecido com um corpo negro é uma cavidade que possui uma pequena abertura por onde entra a radiação.
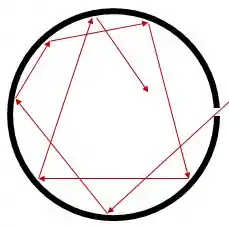
Essa radiação sofre tantas reflexões que tem boas chances de ser absorvida pelas paredes da cavidade antes de sair.
Até aqui, tudo muito lindo... já sabemos como calcular a taxa de energia emitida por um corpo negro... Mas como fazemos pra associar essa energia à frequência?!
Potência Emissiva Espectral de um Corpo Negro
Bonito o nome, hein?
Ok, voltando ao que interessa...
A ideia aqui é calcularmos a taxa de energia emitida por um corpo negro em um determinado comprimento de onda . Essa taxa de energia é dada por:
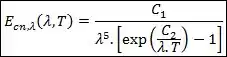
Onde as constantes e são dadas por:
Essa equação é válida para calcularmos a taxa de energia associada a um comprimento de onda, mas não resolve o nosso problema, já que estamos interessados em um intervalo de comprimento de ondas.
Nesse caso, teríamos que integrar essa expressão, usando como limites de integração os comprimentos de onda que estamos interessados.
“Não é possível! Tem que ter um caminho mais fácil!”
Sim, tem!
Função de Radiação do Corpo Negro
Essa função é definida da seguinte forma:
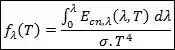
Repare que o denominador é justamente a taxa de energia total emitida por um corpo negro, que nós já calculamos.
Assim, a função de radiação é um valor tabelado que nos ajuda a calcular a taxa de energia emitida em um intervalo de comprimentos de onda de até .
Dessa forma, se quisermos calcular a taxa de energia emitida por um corpo negro entre dois comprimentos de onda e , basta fazer o seguinte:
Dessa forma:
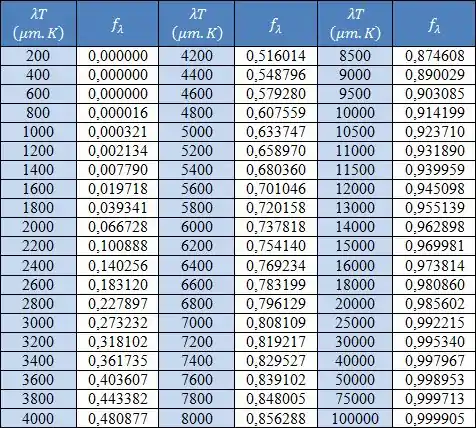
Os valores da função de radiação são dados na tabela abaixo:
Voltando ao problema...
Considerando o intervalor de comprimentos de onda de , teremos:
Olhando para a tabela, teremos:
Logo, a taxa de energia de radiação infravermelha emitida pelo Sol será:
Show de bola! Partiu fixar isso melhor nos exercícios?! Responde Aí! :)
O que é um Corpo Negro?!
Potência Emissiva Espectral de um Corpo Negro E c n , λ
Função de Radiação do Corpo Negro f λ
Voltando ao problema...
Exercícios Resolvidos
Exercício Resolvido #1
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
Considerar uma superfície a uma temperatura uniforme de . Determinar a taxa máxima de radiação térmica que pode ser emitida por esta superfície, em .
Passo 1
Como queremos calcular a taxa máxima de radiação emitida, devemos considerar essa superfície como um corpo negro, dessa forma:
Substituindo os valores, teremos:
Resposta
Exercício Resolvido #2
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
Considerar um corpo cúbico de a suspenso no ar.
Considerando que o corpo se aproxima de um corpo negro, determinar a taxa na qual o cubo emite energia por radiação, em , e a potência emissiva do corpo negro espectral no comprimento de onda de .
Passo 1
Determinar a taxa na qual o cubo emite energia por radiação, em .
A taxa de calor emitida pelo corpo é dada por:
Onde representa a área superficial total do cubo, logo:
Substituindo os valores, teremos:
Passo 2
Determinar a potência emissiva do corpo negro espectral no comprimento de onda de .
Opa! Como estamos preocupados com apenas um comprimento de onda, vamos utilizar a seguinte expressão:
Onde:
Logo:
Resposta
Exercício Resolvido #3
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
(Adaptado) A temperatura do filamento de uma lâmpada incandescente é de . Tratando o filamento como um corpo negro, determinar a fração da energia radiante emitida pelo filamento situada na faixa do visível.
Passo 1
A fração da energia radiante emitida pelo filamento corresponde justamente à função de radiação do corpo negro, definida por:
Agora temos que determinar os valores das funções de radiação.
Passo 2
Obs.: Os valores acima foram encontrados interpolando os valores da tabela na Teoria.
Dessa forma, temos que:
Resposta
Exercício Resolvido #4
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
Uma lâmpada incandescente deve emitir pelo menos 15% de sua energia em comprimentos de onda mais curtos que .
Determinar a temperatura mínima na qual o filamento da lâmpada deve ser aquecido.
Passo 1
Quando o problema nos diz que 15% da energia é emitida para comprimentos de onda menores que , ele basicamente está nos dizendo que:
Assim, se olharmos na tabela, fazendo uma interpolação, veremos que:
Passo 2
Substituindo o valor do comprimento de onda, teremos que:
Resposta
Exercício Resolvido #5
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
O vidro de uma janela de de espessura transmite 90% da radiação entre e e é essencialmente opaco à radiação em outros comprimentos de onda.
Determinar a taxa de radiação emitida através de uma janela de vidro de a partir de fontes de corpo negro a e .
Passo 1
A taxa de energia emitida através da janela é dada por:
Onde:
Logo:
Já podemos tratar de cada caso separadamente.
Passo 2
.
Nesse caso:
Logo:
Passo 3
.
Dessa forma:
Resposta
Exercício Resolvido #6
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptada) Estime a fração da emissão solar que se encontra nas seguintes regiões espectrais: ultravioleta , visível e infravermelha . Considere a temperatura do Sol como .
Passo 1
A fração da banda de emissão de uma região entre os comprimentos de onda e é dada por:
Assim, para a radiação ultravioleta :
Dessa forma:
Passo 2
Para a radiação visível :
Dessa forma:
Passo 3
Para a radiação infravermelha :
Dessa forma:
Resposta
Exercício Resolvido #7
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
O olho humano, assim como produtos químicos sensíveis à luz em filmes fotográficos coloridos, respondem de forma diferente a fontes de luz com distribuições espectrais diferentes.
A iluminação diurna corresponde à distribuição espectral do disco solar, que pode ser aproximado como sendo um corpo negro a . A iluminação incandescente das lâmpadas de bulbo caseiras comuns corresponde aproximadamente à distribuição espectral de um corpo negro a .
Calcule as frações da banda de emissão da região visível, (azul) a (vermelho), para as duas fontes de iluminação.
Passo 1
A fração da banda de emissão de uma região entre os comprimentos de onda e é dada por:
Assim, para :
Observação, para encontrar o valor de , consulte a tabela disponível na teoria.
Para , o valor de não está definido, então é preciso fazer uma correlação linear dos valores de correspondentes para e .
Dessa forma:
Passo 2
Para :
Dessa forma:
Resposta
Para :
Para :
Exercício Resolvido #8
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Câmeras de imagens térmicas têm detectores de radiação que são sensíveis a uma região espectral e fornecem imagens em preto e branco ou coloridas com sombreados para indicar diferenças relativas de temperaturas na cena.
As imagens, que possuem aparência similar às de uma câmera de vídeo portátil, têm numerosas aplicações, tais como na manutenção de equipamentos para identificar motores ou transformadores elétricos superaquecidos e no serviço de combate a incêndios para determinar a direção do espalhamento do fogo e no auxílio da procura e resgate de vítimas.
As regiões espectrais de operação mais comuns são de a e de a . A deleção de uma determinada região depende tipicamente da temperatura da cena, embora as condições atmosféricas (vapor d'água, fumaça, etc) possam também ser importantes.
Determine as frações da banda de emissão de cada uma das regiões espectrais, de a e de a , para as temperaturas de e .
Passo 1
A fração da banda de emissão de uma região entre os comprimentos de onda e é dada por:
Assim, para :
Dessa forma:
Passo 2
Para :
Dessa forma:
Resposta
Para :
Para :