Circuitos de Mais de uma Malha
Produzido por Bruno SoaresTeoria
Introdução
Até agora a gente sabe resolver circuitos de malha simples ou usando o processo da resistência equivalente para circuito com mais de uma malha.
Acontece que nem sempre usar o método da resistência equivalente vai resolver o nosso problema mais rápido. Dá uma olhadinha nesse circuito aqui:
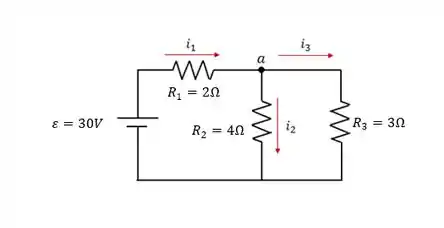
Se a nossa meta é calcular a corrente em todos os ramos, será que dá pra resolver isso rápido fazendo a resistência equivalente?

Essa parada ia demorar pra caramba, portanto vamos aprender um novo jeito de lidar com esse circuito aí, vem comigo!
Regra dos Nós (Lei dos nós de Kirchhoff)
A soma das correntes que entram no nó é igual à soma das correntes que saem do nó.
Vamos aplicar a Lei dos Nós nesse circuito:
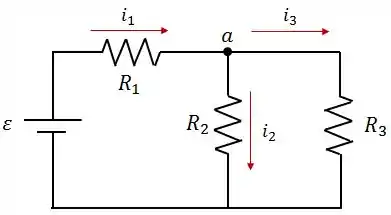
Olhando para o nó , vemos que a corrente está entrando no nó, enquanto as correntes e estão saindo, logo:
Ou você poderia ver isso desse jeito ainda:
Onde positivas são as correntes que saem do nó e negativa é a que entra no nó.
É basicamente isso. Sem muito mistério, né?!
Regra das Malhas (Lei das malhas de Kirchhoff)
Eu sei que já falamos dela em circuitos de uma malha, mas é uma boa dar uma relembrada pra sabermos como aplicar nesses casos.
A soma de todas as diferenças de potencial quando você percorre uma malha é igual a zero.
Vamos aplicar a Regra das Malhas no mesmo circuito de antes:
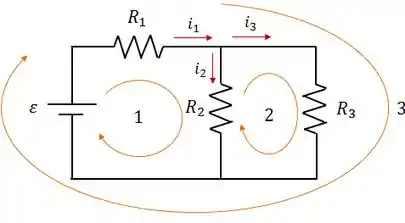
Nós podemos dividir o circuito em 3 malhas:
- Malha 1:
- Malha 2:
- Malha 3:
Substituindo nossos valores: , e temos:
Substituindo e
Substituindo os valores temos:
Em circuitos com mais de uma malha, quase sempre teremos que resolver um sistema no final das contas. Mas a Lei dos Nós já quebra um galhão porque:
Analisando as nossas equações, teremos um sistema com 3 incógnitas e 4 equações. Vamos pegar a equação 2 e usar na equação 4 e tiraremos outra relação de com .
Usando essa relação encontrada acima, na equação (3) temos:
Enfim isolando
Usando a relação de e temos:
Por fim usando a equação da lei dos nós:
Repara que todos os valores de corrente foram positivos, mas se algum valor negativo aparecer não entre em pânico. Basicamente significaria que adotamos o sentido errado na figura e aí era só indicar que o sentido é diferente.
Bora fazer uns exercícios?