Resistência em Série e em Paralelo
Produzido por Bruno SoaresTeoria
Os circuitos que vamos encontrar na prática nem sempre são simples, muitas vezes a gente vai encontrar resistores associados em série e em paralelo! Assim:
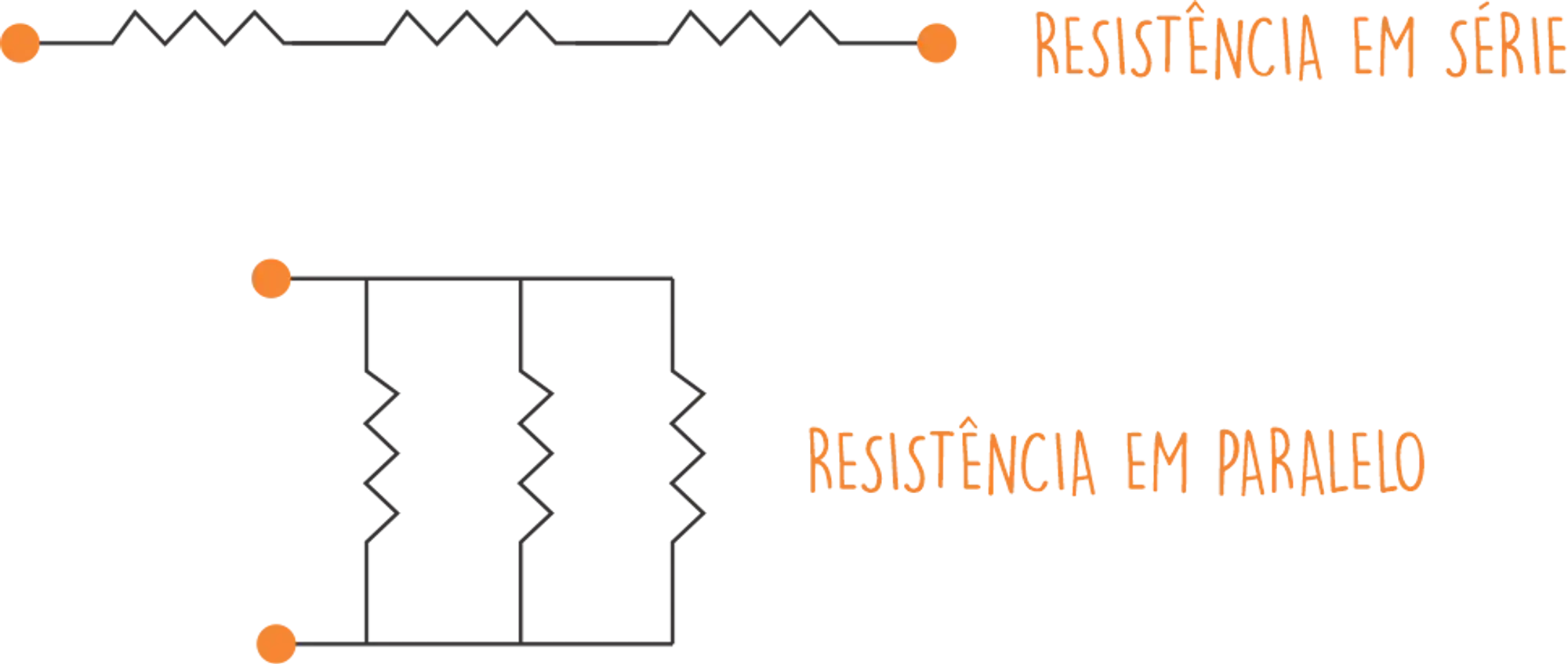
📢 Clique para ver mais:
- Resistência em Série e em Paralelo: Exercícios Resolvidos
- Fórmulas de Eletricidade
- Leis de Kirchhoff
Resistência em Série
Como a gente poderia encontrar a corrente de um circuito onde a associação dos resistores é feita em série?! Vamos olhar o circuito abaixo pra entender melhor isso.
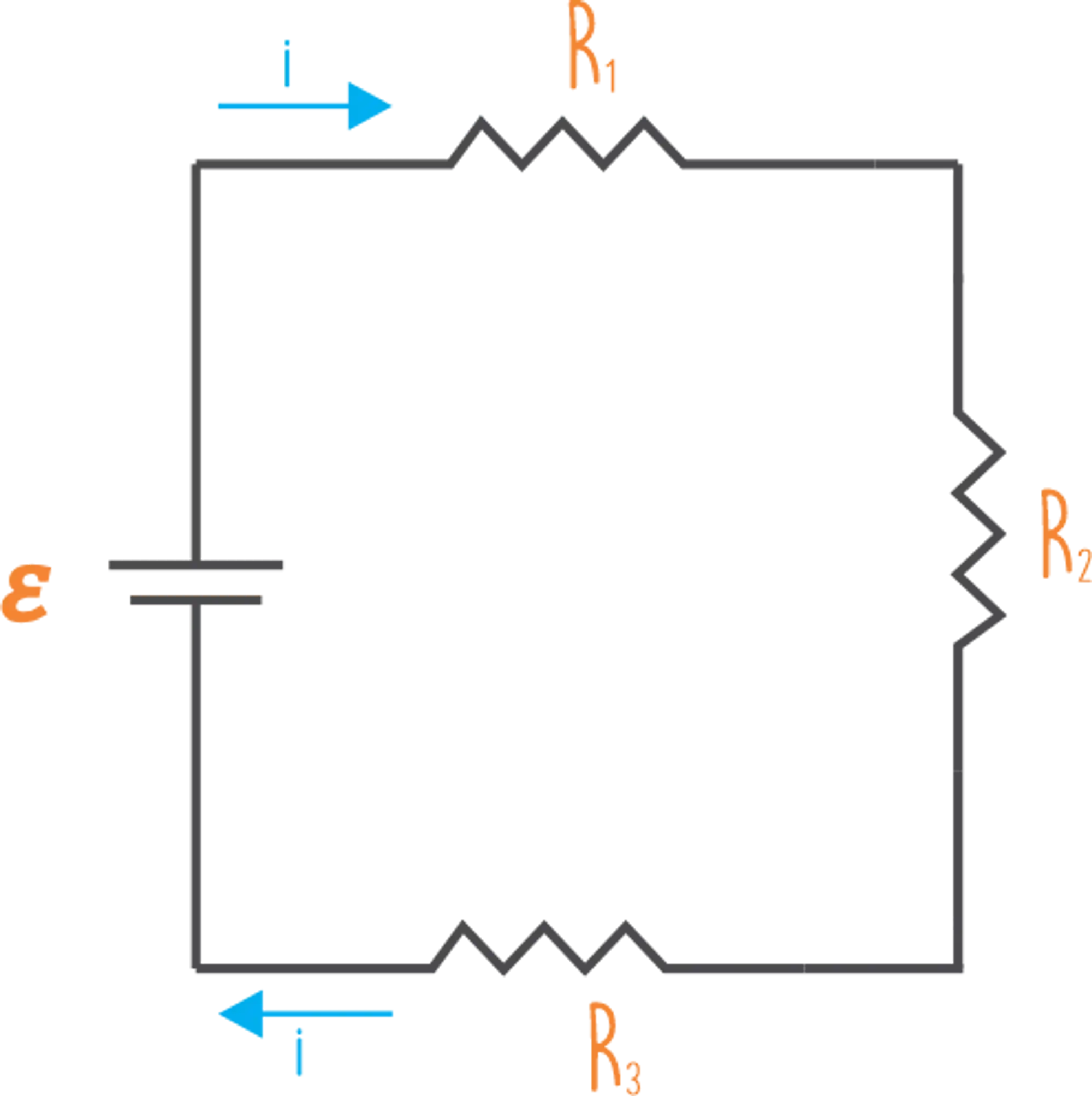
Em um circuito onde os resistores estão associados em série temos a mesma corrente percorrendo todos os resistores, então podemos dizer que:
Já a tensão é dividida entre os resistores, dessa forma temos:
Resistência em Série: Como Calcular a Resistência Equivalente
Beleza, mas como eu faço para calcular a resistência equivalente?!
Nesse caso tudo o que você tem que fazer é somar todas as resistências, assim:
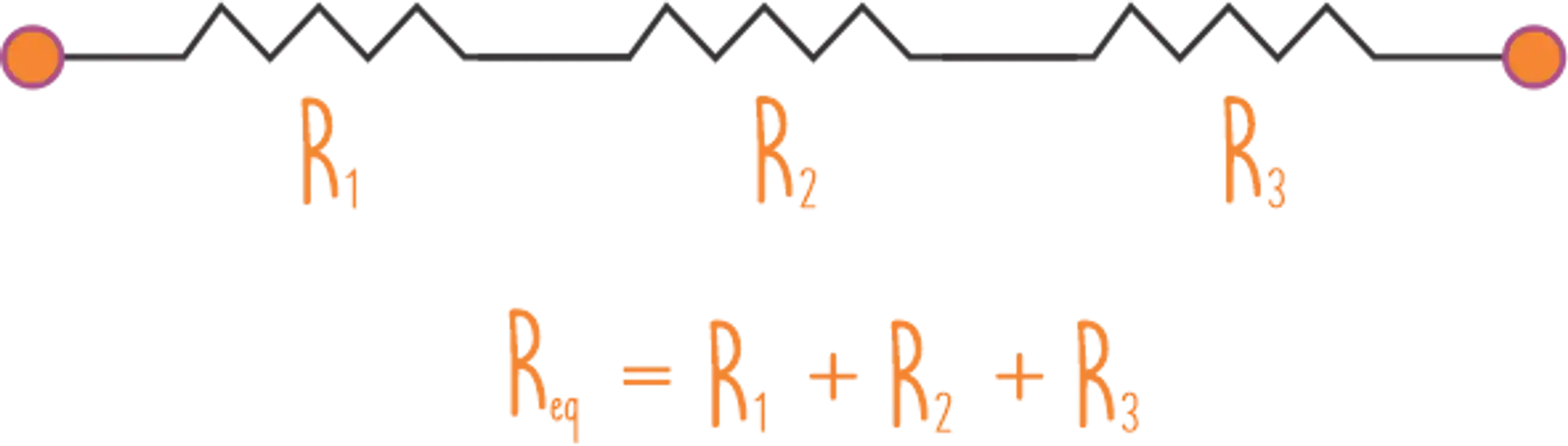
Resistência em Paralelo
Agora a gente vai analisar um circuito com resistores ligados em paralelo! Nesse caso a corrente tem vários caminhos pra percorrer, sendo assim em cada resistor ligado em paralelo tem uma corrente diferente, mas a diferença de potencial para eles é a mesma. Se liga na imagem abaixo:
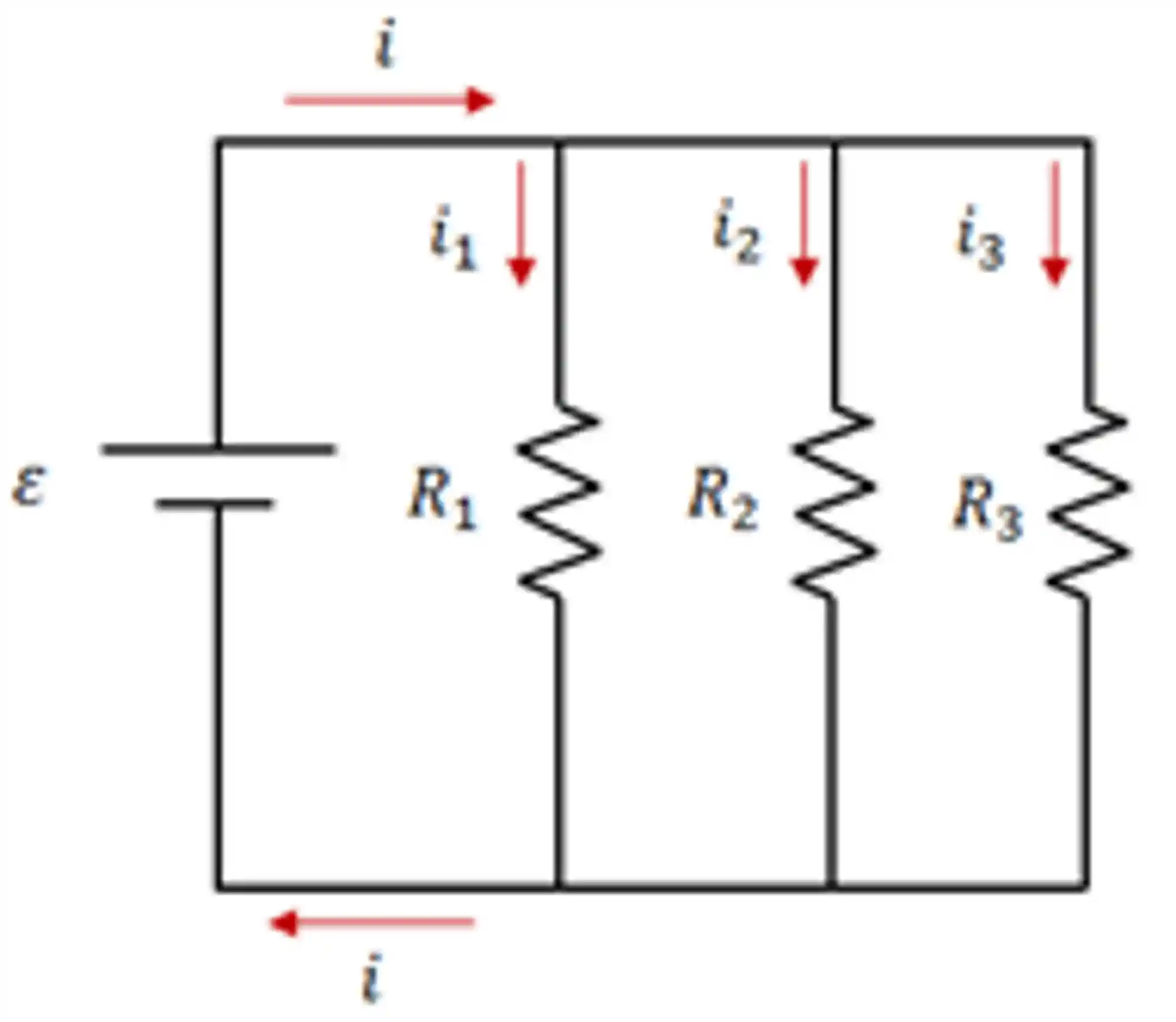
Para a resistência em paralelo podemos dizer que:
Resistência em Paralelo: Como Calcular a Resistência equivalente
Se a corrente equivalente é igual a soma de todas as correntes e a tensão equivalente é igual em todos os resistores, temos que:
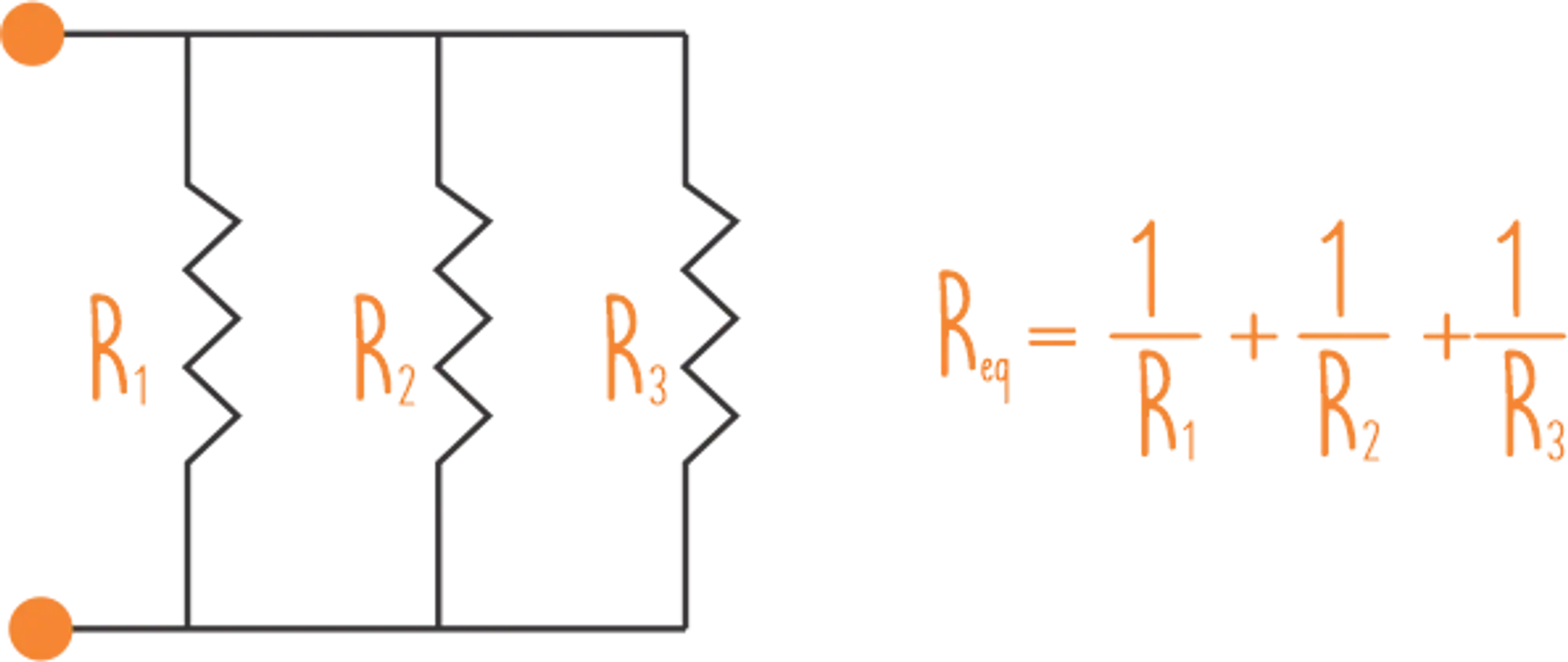
Você também pode conferir esse conteúdo em vídeo:
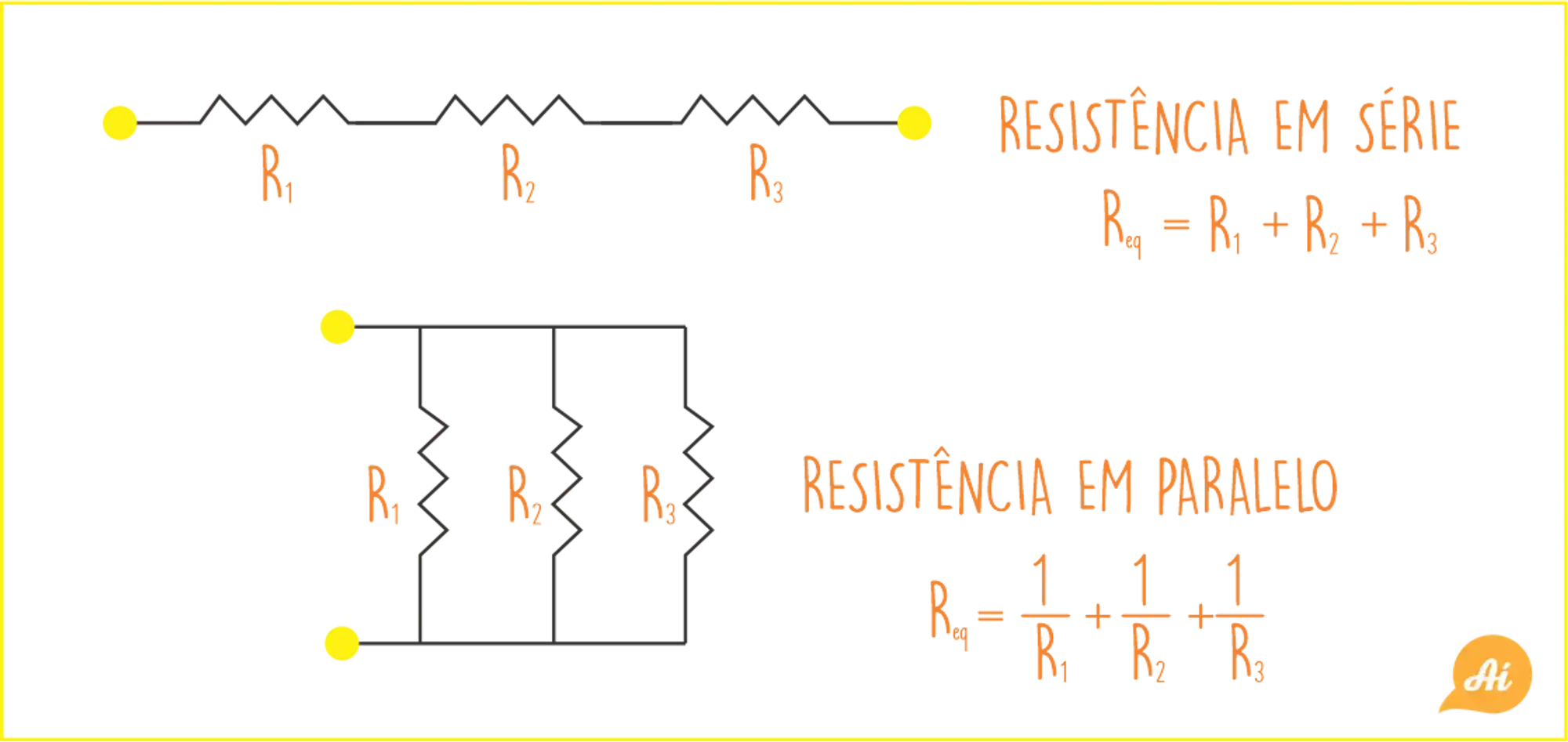
Resumo: Fórmulas das Resistências Equivalentes
Agora pra acabar, um resuminho:
Vamos praticar com exercícios?
Resistência em Paralelo
Resumo: Fórmulas das Resistências Equivalentes
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2006, pp 189-9.
Pretende-se obter uma resistência total de ligando uma resistência de valor desconhecido a uma resistência de . Qual deve ser o valor da resistência desconhecida?
Passo 1
Opa! Começando os exercícios desse tipo devemos prestar atenção em algo bem sutil aqui pra resolver essa questão.
Ele fala que e que . A resistência equivalente é menor que uma das resistências. Isso implica dizer que teremos uma ligação em paralelo com um resistor que vou chamar de , pois se a ligação fosse em série a soma seria maior que .
Passo 2
Para resistências em paralelo, teremos:
Resposta
Exercício Resolvido #2
UFF- Lista de Exercícios sobre Circuitos Elétricos- Questão n° 9.
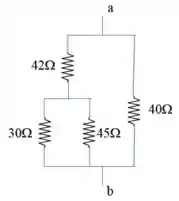
Qual é a resistência equivalente do circuito da figura?
Passo 1
Para determinar a resistência equivalente, vamos começar da parte mais “interna” que podemos resolver, nesse caso, as resistências de e que estão em paralelo. Para resistências em paralelo, temos:
Agora, temos que essa resistência equivalente está em série com a resistência de , para resistências em série, temos:
Agora, temos que essa resistência está em paralelo com a resistência de , teremos então:
Resposta
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2006, pp 197-81.
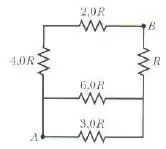
Na figura abaixo . Qual é a resistência equivalente entre os pontos e ?
Passo 1
Temos mais um circuitinho cheio de resistores meio confusos. Mas bora lá!
A primeira coisa que podemos fazer aqui, e que não é difícil de perceber é calcular a resistência equivalente nesses dois resistores abaixo. Como o resistor de e estão em paralelo, teremos:
Passo 2
Assim que a gente fez isso, vamos ter o seguinte circuito equivalente.
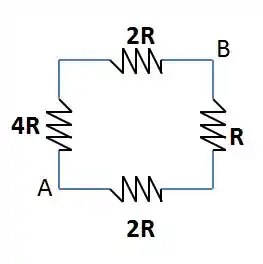
Entre o terminal A e B, pelo ramo superior vão ficar o resistor de em série com o de e no ramo inferior vai ficar em série com . Dá pra sacar, né?
Assim, poderemos escrever:
Passo 3
E vai sobrar isso aqui, oh!
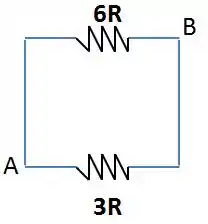
Dois resistores paralelos entre A e B. Tudo que a gente precisa pra terminar a nossa questão.
Resposta
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2006, pp 191-26. Modificada.
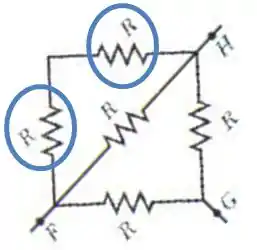
A figura abaixo mostra cinco resistores de . Determine a resistência equivalente
a) entre os pontos F e H;
b) entre os pontos F e G.
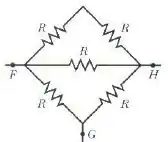
Passo 1
Vixi! Olhando assim de primeira da até uma dor de cabeça!
Mas calma, acho que tem como desenhar isso de uma forma melhor e as contas vão se simplificar. Se liga aí!
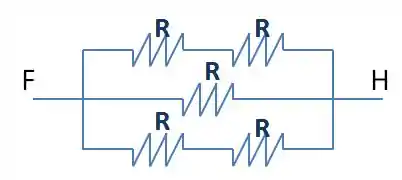
Isso aqui e a figura do enunciado são o mesmo circuito só que um pouco mais linear.
Melhorou né? Agora ficou tranquilo de calcular.
Passo 2
Para resistências em paralelo, teremos:
De onde vieram esses ? Das resistências em série que estão localizadas na parte superior e inferior dos fios.
Continuando, vai ficar:
Passo 3
b)
Aqui fica um tantinho mais complicado. Mas Keelp Calm and Vamos lá!
Primeiro de tudo vamos prestar atenção nesses dois resistores.
É fácil de ver que eles estão em série, né? Logo a ali é igual a .
Podemos perceber também que eles estão em paralelo com o resistor que está entre F e H, certo? Por conseguinte isso que sobrar está em série com o resistor que está entre G e H. A resistência equivalente de tuuudo isso estará em paralelo com o resistor entre F e G e daí acabamos a questão.
Passo 4
Ficou confuso? Vamos por partes.
O que a gente já tem é isso aqui:
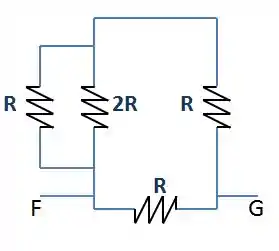
Calculando ali na esquerda esses resistores em paralelos, teremos:
Passo 5
E aí nosso circuito se tornará:
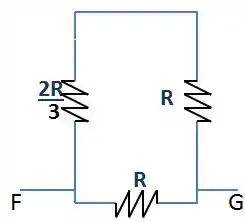
Agora, o resistor da direita com o da esquerda estão em série. Basta soma-los.
Passo 6
É. Daquele monstrão lá agora só sobrou isso aqui.
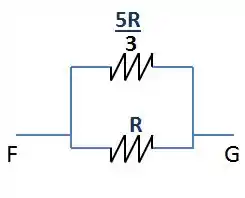
E circuitos em paralelo assim você já está careca de saber calcular.
Resposta
Exercício Resolvido #5
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2006, pp 198-88.
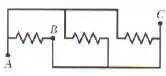
A figura abaixo mostra três resistores de . Determine a resistência equivalente
- entre os pontos A e B;
- entre os pontos A e C;
- entre os pontos B e C;
Passo 1
Essa questão é bem famosinha. Várias faculdades colocam ela em listas de exercícios. A princípio ela se parece esquisita mas jajá você vai ver que ela é simples.
Presta bem atenção!
Perceba que acima do ponto A até chegar no último resistor da direita não nada entre eles. Isso significa que eles são pontos equipotenciais, ou seja, com mesmo potencial.
A mesma coisa podemos dizer para o fio que sai de B e vai pra C. Não tem nada entre eles, então podemos dizer que o potencial de B é igual ao potencial em C.
Passo 2
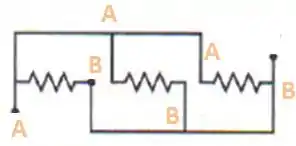
E mais,como vou mostrar na figura abaixo, a gente vai poder ver que todos os três resistores estão ligados entre A e B.
Saca só!
Passo 3
Podemos redesenhar o nosso circuito de uma forma bem melhor.
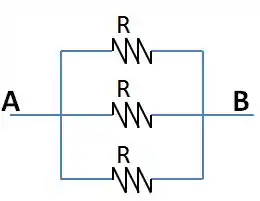
Agora ficou fácil,né?
Passo 4
b)
Como a gente já viu que o ponto B e o ponto C são os mesmo, a resistência equivalente vai ser igual, logo:
Passo 5
C)
Se o ponto B e C são os mesmos, significa dizer que não tem nenhuma resistência entre eles, logo:
Resposta
Exercício Resolvido #6
USP-P2-2012-Questão n°2
Um resistor cilíndrico de comprimento deveria ter uma seção reta ao longo de todo seu comprimento e uma resistência igual a . Devido a um erro de fabricação, metade do resistor apresenta uma seção reta , conforme a figura.
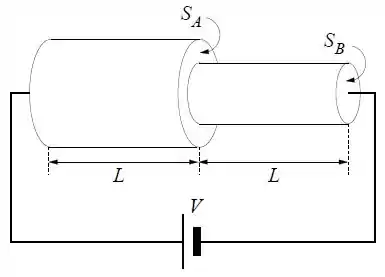
Determine a resistência do resistor em termos do valor projetado .
Aplica-se uma ddp de volts nas extremidades do resistor. Calcule os módulos dos campos elétricos e em cada um dos trechos do resistor em termos de e .
Passo 1
Determine a resistência do resistor em termos do valor projetado .
Bom, se esse cara fosse construído da mesma forma que foi planejado, com área transversal e comprimento , a sua resistência seria dada por:
Beleza! Mas alguém fez merda e o resistor saiu com essa cara...
Vamos pensar o seguinte... se vem uma corrente da esquerda para a direita, ela vai passar primeiro pela parte do resistor com área transversal e depois pela parte do resistor com área transversal , concorda?
Então seria a mesma coisa dizer que esses dois caras estão em série, conseguiu enxergar isso?
Assim, a resistência será:
O problema já nos disse que . Então voltando ao problema:
Nós já achamos ali em cima que:
E como temos que comparar com , vamos tentar dar uma arrumada no pra poder substituir o :
Passo 2
Aplica-se uma ddp de volts nas extremidades do resistor. Calcule os módulos dos campos elétricos e em cada um dos trechos do resistor em termos de e .
Quando aplicamos a ddp nas extremidades do resistor, deve ser igual à soma das ddps de cada uma das duas partes do resistor.
Além disso, podemos associar a ddp com o campo elétrico através da relação , logo:
Agora que já encontramos a relação entre , e , precisamos descobrir uma relação entre e .
Como esses dois caras estão em série, a corrente que passa pelas duas partes deve ser a mesma , assim, através da Lei de Ohm:
Novamente vamos usar a relação que o problema nos deu, :
Agora ficou fácil! Vamos substituir isso na expressão de para encontrarmos e em função de e .
Passo 3
Começando por:
Teremos:
Beleza! Para encontrar temos apenas que fazer a substituição inversa:
Portanto:
Resposta
Exercício Resolvido #7
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 26.14, pp. 194.
Considere o circuito indicado na Figura abaixo. A corrente que passa pelo resistor de é igual a no sentido indicado. Quais são as correntes que passam pelos resistores de e ?
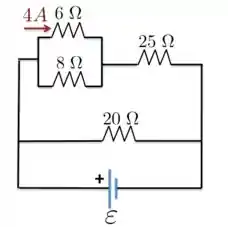
Passo 1
Para começar o exercício, dá uma olhada na Figura abaixo, e repara que a gente tem, além da corrente dada no enunciado de , as correntes e . Para começar, as correntes de e se somam no ponto para dar a corrente , isto é,
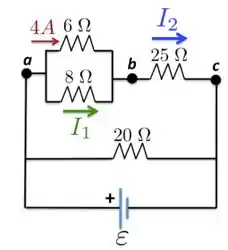
Agora, entre os pontos e , temos dois resistores em paralelo. Isso significa, como já vimos na teoria, que esses resistores estão à mesma diferença de potencial . No resistor de , a ddp é de
Portanto, como essa é também a ddp para o resistor de , então
Disso, temos que a corrente que passa no resistor de é
Passo 2
Então, para completar nossa solução do exercício, repara lá na Figura que o resistor de está à mesma diferença de potencial que tem os resistores entre os pontos e , então:
Para a gente saber que ddp é essa, podemos encontrar a resistência equivalente entre os pontos e por onde passa a corrente total . Então, os resistores de e estão em paralelo e o resultado disso está em série com o de , concorda?
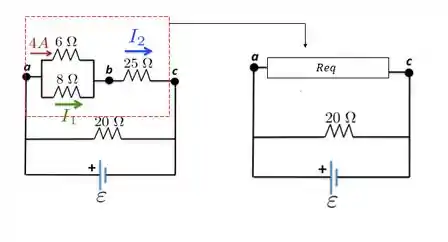
Bom, colocando isso em contas, temos
Portanto, a ddp entre as extremidades do resistor de é
Então, a corrente que passa pelo resistor de é
Resposta
No resistor de passa uma corrente de
e no de , uma de
Exercício Resolvido #8
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 26.20, pp. 194.
No circuito indicado na Figura abaixo, a taxa de dissipação da energia elétrica de é igual a .
- Determine e .
- Qual é a fem da bateria?
- Ache a corrente que passa por e pelo resistor de .
- Calcule o consumo total de energia elétrica em todos os resistores e a energia elétrica fornecida pela bateria. Mostre que seus resultados estão de acordo com a conservação de energia.
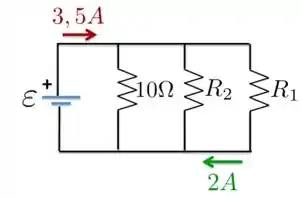
Passo 1
a) Então, vamos lá? Bom, para começar, o enunciado dá o valor da potência dissipada no resistor , que é de , e conhecemos da Figura o valor da corrente que passa nesse resistor,
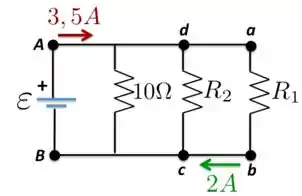
Agora que temos o valor dessa resistência, podemos encontrar o valor do potencial entre os pontos e , que a mesma ddp entre os resistores e , ambos em paralelo com . Portanto
Essa é ddp da resistência equivalente , por onde passa a corrente de mostrada na Figura. Concorda? Checa isso para ver se faz sentido....checou?
A resistência equivalente nesse caso é
Simplificando essa expressão, obtemos que
Essa resistência está submetida à uma ddp de , o que dá pra gente que
Resolvendo essa equação, temos que é
Passo 2
b) A fem da bateria é a mesma a que está a resistência equivalente que, por sua vez, é a mesma que está entre os pontos e . Então,
Passo 3
c) Como o resistor está a uma ddp de , então a corrente que passa por esse resistor é
Pelo resistor de , que também está a uma ddp de , a corrente é
Passo 4
d) A potência total fornecida pela bateria é
A potência dissipada pelo resistor é de . Já no resistor , a potência dissipada é de
No resistor de , a potência é
Se a gente soma todas as três potências dissipadas em cada resistor, teremos exatamente o valor de , que é o valor total da potência fornecida pela bateria. Isso mostra que há conservação de energia