Amperímetro e Voltímetro
Produzido por Bruno SoaresTeoria
Fala aí, você ta no Responde Aí! E aqui você vai aprender tudo que precisa sobre Amperímetro e Voltímetro
Você já pensou: Como engenheiros e cientistas fazem medidas elétricas? Pra isso precisamos de equipamentos para medir corrente e tensão elétrica.
Assim como podemos usar uma régua para medir distâncias, podemos usar o amperímetro para medir corrente elétrica, e o voltímetro para medir tensão elétrica.
Amperímetro
Um amperímetro é um aparelho que mede a corrente elétrica em um determinado ponto do circuito.
Na hora de usar o amperímetro é colocado em série com os resistores e ele vai nos dizer qual é a corrente em amperes naquele ponto.
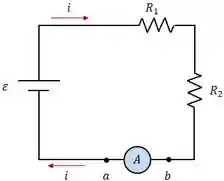
Um amperímetro ideal tem resistência zero para poder não interferir na medição da corrente e é colocado em série com o elemento de circuito que se quer estudar.
Em um amperímetro real, é essencial que a sua resistência seja muito pequena em comparação com as outras resistências do circuito.
Exemplo de questão de amperímetros
Um circuito possui dois resistores
a) Qual a corrente medida por um amperímetro ideal?
b) Qual a corrente medida por um amperímetro real com resistência de
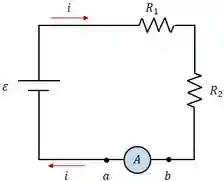
Passo 1: Vamos fazer primeiro considerando o amperímetro ideal.
Aplicando a lei das malhas, a gente gera a seguinte equação pro circuito:
Porém, a resistência de um amperímetro real é zero R_{amperimetro}=0, então:
Logo:
Passo 2: Agora vamos considerar o amperímetro real.
Novamente utilizando a lei das malhas, encontramos a mesma equação:
Porém, esse é um amperímetro real, e por isso não podemos ignorar sua resistência, então, vamos reorganizar a equação:
Como esse é um amperímetro real, nós temos que considerar sua resistência interna, logo:
Ou seja, para qualquer circuito, sempre vai existir uma diferença entre a corrente ideal e real medida pelo amperímetro!
Voltímetro
Já o voltímetro é um equipamento usado para medir a voltagem em algum ponto do circuito.
O voltímetro é colocado em paralelo com um resistor e vai funcionar como uma outra resistência em paralelo, lembra que resistores em paralelo possuem a mesma voltagem?
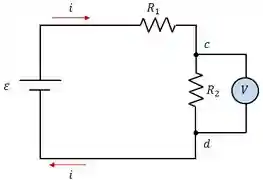
Para medir corretamente a tensão, um voltímetro ideal deve ter uma resistência infinita, para não deixar nenhuma corrente passar por dentro dele.
Mas é impossível ter resistência infinita, então um voltímetro real possui uma resistência muito mais alta que a do restante do circuito.
Exemplo de questão de voltímetro
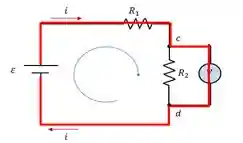
Um circuito possui dois resistores
a) Qual a tensão medida por um voltímetro ideal?
b) Qual a tensão medida por um voltímetro real com resistência de
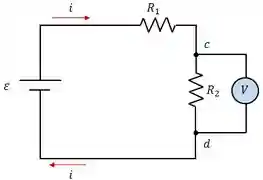
Passo 1: Vamos analisar o voltímetro real. Nesse caso a gente pode considerar que a resistência é infinita e por isso não temos nenhuma corrente passando pelo voltímetro.
Então na hora de aplicar a lei das malhas, podemos simplesmente ignorar o voltímetro ideal.
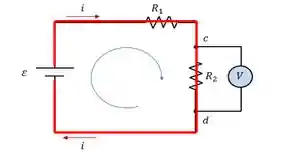
O resultado é que o circuito passa a ser em série como se não existisse o voltímetro ali
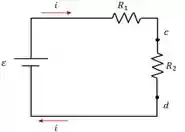
E como o voltímetro está em paralelo com a resistência
Então a tensão medida pelo voltímetro ideal é:
Passo 2: Com o voltímetro real, a coisa é um pouco diferente, pois precisamos considerar que existirá uma corrente passando pelo instrumento.
Então vamos precisar usar a lei das malhas para resolver o circuito. Primeiro, vamos considerar a malha que passa por pelo resistor
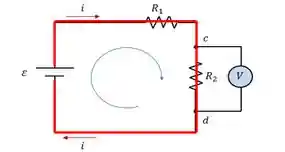
E depois consideramos a malha que passa pelo voltímetro real:
E como
Igualando as equações das duas malhas temos:
E aplicando isso na equação das correntes vamos ter:
Isolando
Show! Agora, como sabemos que a tensão sobre
Logo, a tensão medida pelo voltímetro real é:
Resumo:
- A diferença entre amperímetro e voltímetro é que o amperímetro mede corrente elétrica e o voltímetro mede tensão elétrica
- Para todos os circuitos a corrente ideal é sempre maior que a real (
), ainda que a diferença seja pequena. - Para todos os circuitos a tensão ideal é sempre maior que a real (
), ainda que a diferença seja pequena.
Videoaula
Pra garantir que você vai saber de tudo que precisa pra sua prova, da uma olhada na nossa videoaulas:
Agora rola pra baixo 👇 e vamos fazer uns exercícios!
Resistores