Cálculo do Momento de Inércia em Corpos Extensos

Teoria

Introdução:

Belezoca galerinha, até agora vimos como calcular o momento de inércia para partículas no espaço, mas agora imagine que o Dexter Pizzaiolo está querendo abrir a massa de uma pizza com um rolo de pizza:

Nesse caso o rolo pode ser considerado um cilindro, e temos que o Dexter vai abrir a massa fazendo o rolo girar em torno do eixo que passa pelo seu centro de massa:

Então nessa situação, qual seria o momento de inércia do rolo de pizza?

Bom galerinha, se o cilidro fosse uma partícula, poderíamos medir sua massa pontual e calcular a distância até o eixo de rotação, para descobrir o momento de inércia aplicando a fórmula:

MAAAASSSS, o cilindro possui dimensões como o raio e o comprimento que não nos deixa considerá-lo como uma partícula.

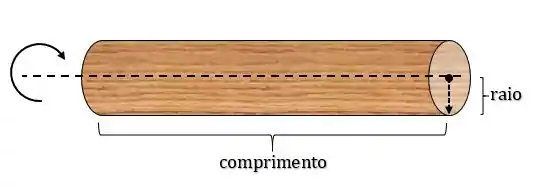
Nesse caso sua massa está distribuída por todo o corpo, com uma distância variando pra cada pedacinho de massa. Sendo assim, precisaremos tentar outra abordagem para calcular esse momento de inércia. Bora lá ver isso direitinho!!

Cálculo do Momento de Inércia de Corpos Rígidos:

Iradoso galerinha, pra gente compreender legal esses conceitos, vamos pegar um exemplo de uma barra homogênea de massa e comprimento que gira em torno de um eixo que passa pelo seu centro de massa:

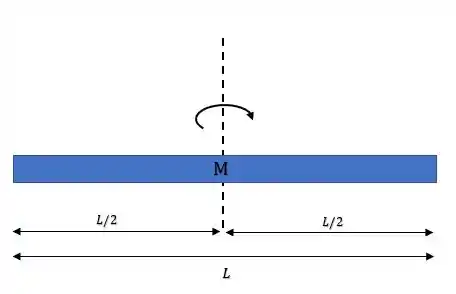
Nessa situação, temos que cada pedacinho de massa da barra, vai possuir um momento de inércia em relação ao eixo de rotação:

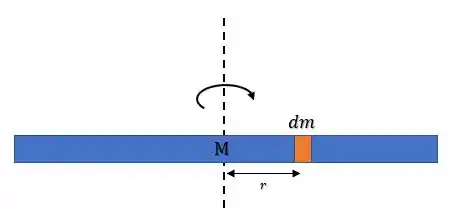
Esse momento de inércia do pedacinho pode ser escrito como:

Onde é a distância desse pedacinho até o eixo de rotação. A malandragem disso tudo, é que temos infinitos pedacinhos de massa dentro da barra, de maneira que o momento de inércia total da barra, será a soma de todos esses infinitos momentos de inércia.

Ou seja, podemos lembrar lá das aulinhas de cálculo, e usar os conceitos de integral para calcular esse momento de inércia total , de maneira que a soma de todos esses momentos de inércia menores, será dada como:

A parada importante aqui, é que sempre a gente deve tentar relacionar aquele pedacinho de massa com a distância , afinal é nossa variável na conta. Sendo assim, podemos usar o fato da barra ser homogênea, de forma que a densidade linear é igual em todos os pontos, isto é, para a dimensão da barra de massa , temos uma densidade:

Agora se a gente tem um pedacinho de massa sob um pedacinho de distância :

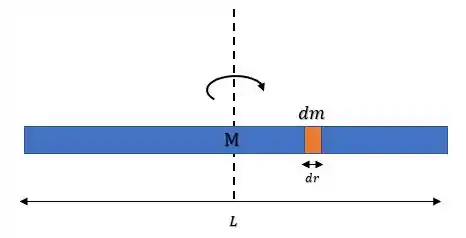
Iremos obter que a densidade linear da barra será:

Então igualando as duas expressões, obtemos que:

Então substituindo na nossa integral:

E como a distância varia no eixo como na figura abaixo:

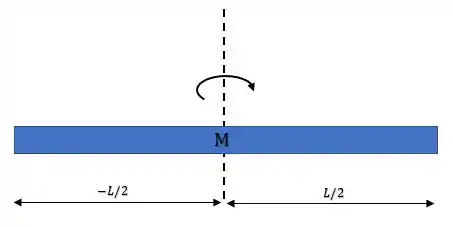
Os limites de integração será:

Resolvendo essa integral, obtemos que o momento de inércia da barra será:

Momento de Inércia Tabelados:

Parece complicado essa continha que a gente fez né?

Mas poucas vezes a gente vai precisar realizar todo esse processo, porque alguém já fez isso uma vez rsrs!

Se liga nessa tabela com os momentos de inércia das formas mais comuns.

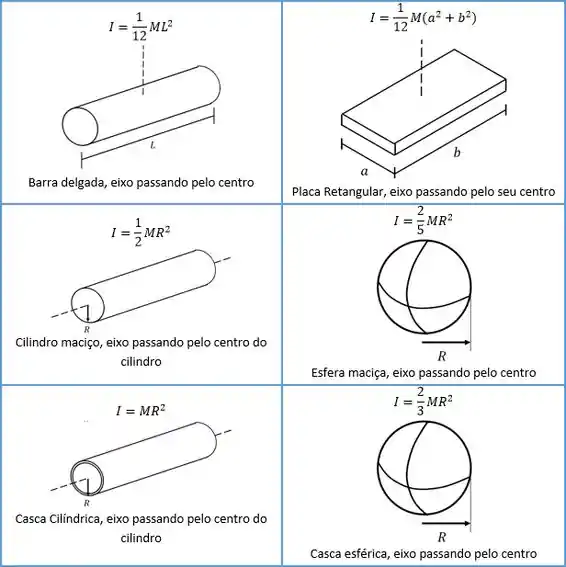
Ou seja, sempre que temos um corpo conhecido dentro dessa tabela, não precisamos calcular o momento de inércia tudo de novo, é spo a gente vir na tabelinha dar uma bizurada no momento de inércia e aplicar ele na continha hehe bem sagaz!!

Show! Bora praticar!

Cálculo do Momento de Inércia de Corpos Rígidos:

Momento de Inércia Tabelados:

Exercícios Resolvidos

Exercício Resolvido #1

Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 292-91

Mostre que o momento de inércia de um cilindro de massa e raio em relação ao eixo central é igual ao momento de inércia de um aro fino de massa e raio em relação ao eixo central. Mostre que o momento de inércia de um corpo qualquer de massa em relação à qualquer eixo é igual ao momento de inércia de um aro equivalente em torno do mesmo eixo, se o aro tiver a mesma massa e um raio dado por

O raio do aro equivalente é chamado de raio de giração do corpo.

Passo 1

Aprendemos que o cálculo do momento de inércia de corpos extensos é feito por meio de integral, então, a primeira idéia é calcular a integral:

Certo?

Desespero bateu aí né?

Relaxa que papai aqui vai te passar o bizu. O bizu do estripador.

“Estripador? Que que é isso?!”

É aquele cara que faz parte por parte, bem devagar e com calma, então vamos lá!

Passo 2

A primeira coisa a se fazer é calcular o momento de inércia do aro homogêneo de massa e raio , em relação ao eixo central do mesmo.

Aqui podemos usar a integral, pois trata-se de uma integral simples, saca só:

No aro, todas as minipartículas que o compõem estão à mesma distância do eixo de rotação, portanto:

Podemos concluir:

Passo 3

Beleza! Agora, vamos calcular o momento de inércia do cilindro em relação ao eixo central. Vamos considerar um elemento da forma de cilindro no interior do cilindro de massa , raio e comprimento . Esse elemento cilíndrico tem massa , raio e altura , como na figura abaixo.

Devemos considerar também que o cilindro possui uma densidade volumétrica uniforme, de forma que:

Assim, temos que o momento de inércia do cilindro maior pode ser obtido integrando o elemento infinitesimal para de 0 até :

Substituindo pela expressão obtida acima:

Substituindo por :

Passo 4

Agora que já temos o momento de inércia do cilindro e o momento de inércia do aro em relação ao eixo central, vamos voltar ao enunciado.

O momento de inércia de um cilindro de massa e raio é dado por:

O momento de inércia de um aro de massa e raio é dado por:

Logo, eles são iguais! :)

Passo 5

Vamos lá, estamos quase acabando!

Agora o que ele quer que a gente mostre é que o momento de inércia de um corpo de mass em relação a qualquer eixo é igual ao momento de inércia de um aro equivalente de massa e um raio ao redor desse mesmo eixo. Parece complicado, né? Vamos com calma!

Passo 6

Bom, já vimos que o momento de inércia de um aro em relação ao eixo central é dado por:

onde é o raio. Se é dado por , onde é o momento de inércia de um corpo em relação ao mesmo eixo, temos que:

Logo, mostramos que o momento de inércia de um corpo qualquer em relação a um dado eixo é igual ao momento de inércia de um aro em volta desse eixo de raio .