Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Teorema dos Eixos Paralelos

Ver Todos os Exercícios

Teoria

O Teorema dos Eixos Paralelos serve para calcular o Momento de Inércia em corpos em relação a um novo eixo de rotação, que deve ser paralelo ao centro de massa!

Por exemplo, podemos calcular o momento de inércia dessa régua abaixo, em relação à um eixo perpendicular ao centro de massa:

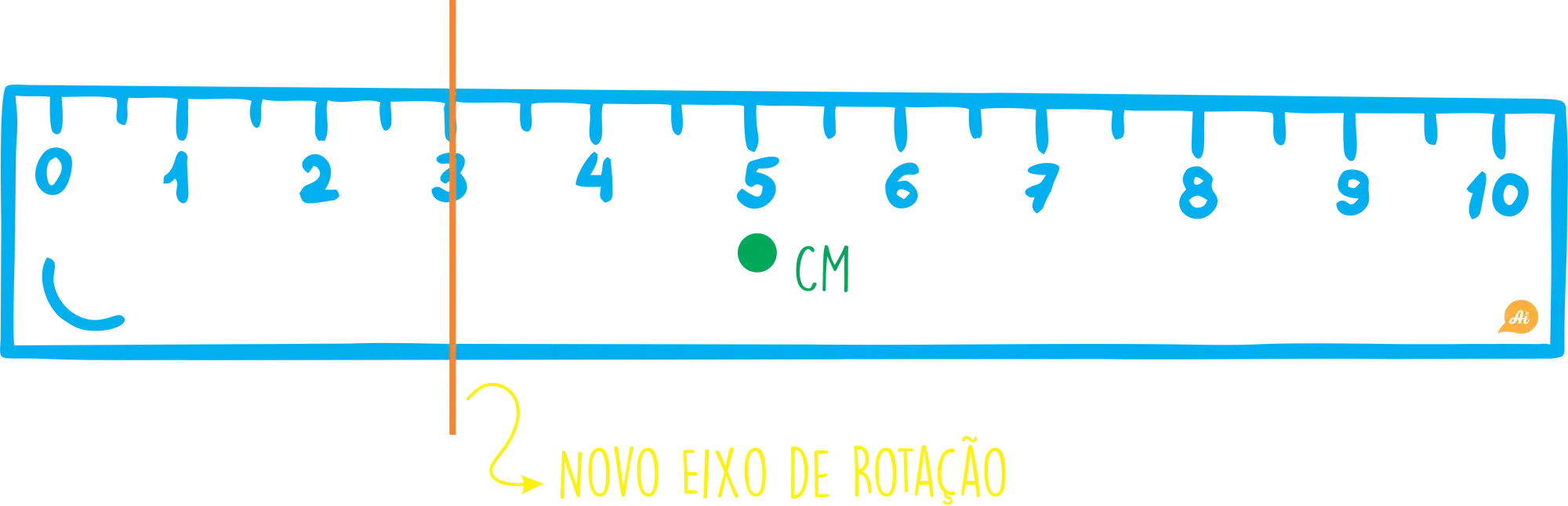
Teorema dos Eixos Paralelos: Exemplo
Teorema dos Eixos Paralelos: Exemplo

O Teorema do Eixo Paralelo diz que:

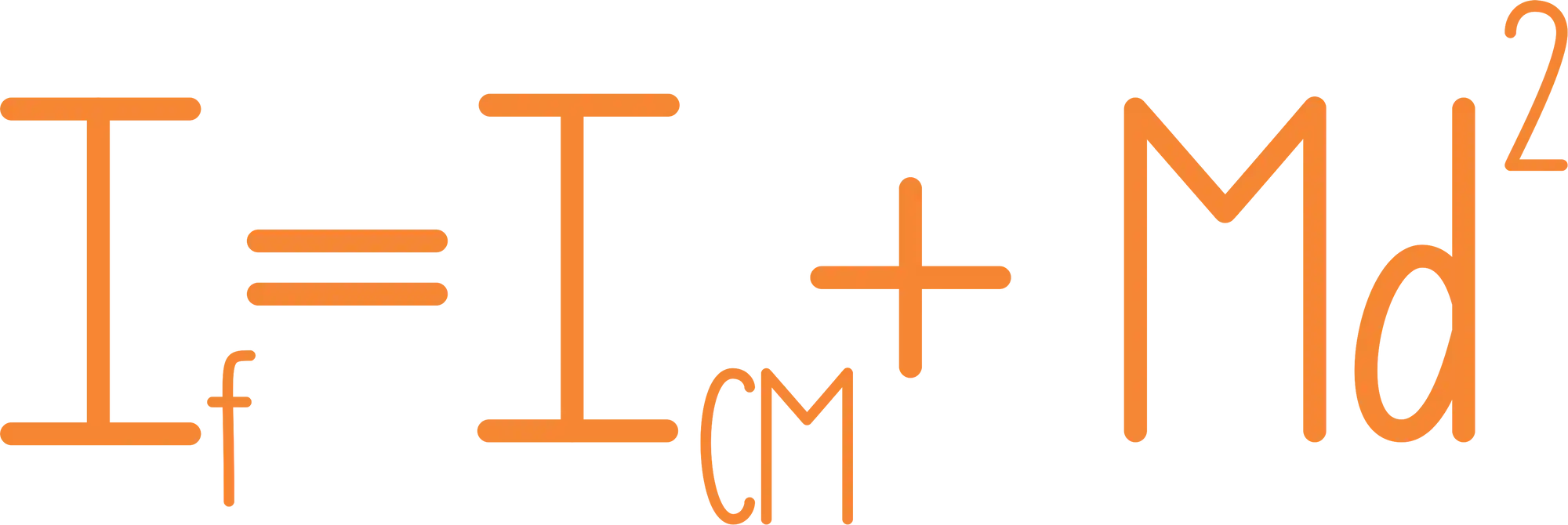
Teorema dos Eixos Paralelos
Teorema dos Eixos Paralelos

Ou seja, tudo o que temos que fazer para achar o momento de inércia em torno de um novo eixo é: Calcular o momento de inércia considerando o centro de massa como eixo de rotação e depois somar esse valor com o produto entre a massa do objeto e o quadrado da distância entre o centro de massa e o novo eixo!

Parece bem tranquilo… mas vamos fazer um exemplo pra entender melhor?!

📢 Clique para ver mais:

Como Usar o Teorema dos Eixos Paralelos para Calcular o Momento de Inércia

Vamos calcular o momento de inércia da nossa régua! Pra isso é importante sabermos que sua massa é igual a . Além disso vamos considerar a régua como uma placa regular na hora de calcularmos o momento de inércia considerando o centro de massa!


Passo 1: Identificar o Eixo de Rotação

O novo eixo deve ser paralelo ao eixo do centro de massa, como podemos observar na figura abaixo:

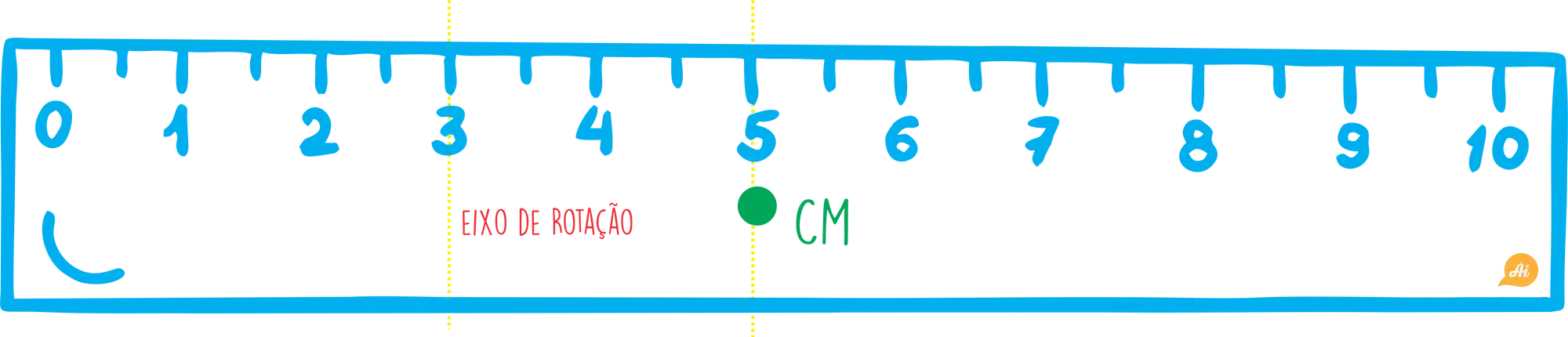
Novo eixo de rotação
Novo eixo de rotação

Passo 2: Identificar qual a distância do eixo de rotação para o eixo que passa pelo centro de massa

Distância entre o eixo de rotação e o eixo que passa pelo centro de massa
Distância entre o eixo de rotação e o eixo que passa pelo centro de massa

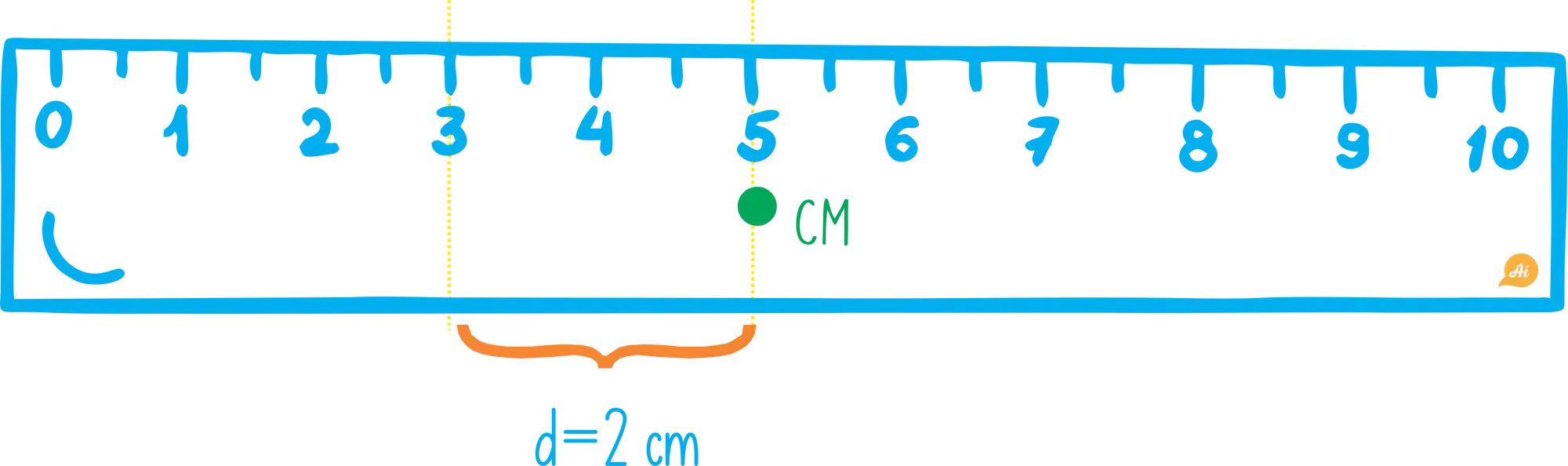
A distância será igual a !

Você também pode ver a resolução desse exemplo no vídeo abaixo:

Exercícios Resolvidos

Exercício Resolvido #1

Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, p. 287-35

Calcule o momento de inércia de uma régua de um metro, com uma massa de 0,56   k g , em relação a um eixo perpendicular à uma régua na marca de 20   c m . (Trate a régua como uma barra fina.)

Passo 1

Neste problema nos foi pedido o momento de inércia em relação a um eixo que não passa pelo centro de massa do corpo, portanto, iremos usar o teorema dos eixos paralelos.

Dá uma olhada na imagem pra facilitar a aplicação:

Passo 2

Nós sabemos que o valor do momento de inércia da régua é igual ao momento de inércia de uma barra homogênea, portanto, o seu I 0 , aquele momento de inércia calculado em relação ao eixo que passa pelo centro de massa é dado por:

I 0 = M L 2 12

Queremos o momento de inércia em relação à um eixo que, como na imagem, dista 30   c m do eixo que passa pelo centro de massa, portanto:

d = 0,3   m

E então, aplicando o teorema, temos:

I = I 0 + M d 2

I = 0,56   .   1 2 12 + 0,56   .   0,3 2

I ≅ 0,097   k g . m 2

Resposta

I ≅ 0,097   k g . m 2

Exercício Resolvido #2

Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 288-41

O bloco uniforme da Fig. 10-37 tem massa de 0,172   k g e lados a = 3,5   c m , b = 8,4   c m e c = 1,4   c m . Calcule o momento de inercia do bloco em relação a um eixo que passa por um canto e é perpendicular às faces maiores.

Passo 1

Em todos os exercícios de cálculo de momento de inércia, devemos primeiramente saber se o que foi pedido não é um resultado conhecido.

Nesse caso, é conhecido o resultado do momento de inércia de um bloco em relação ao eixo que passa pelo seu centro de massa:

I 0 = M a 2 + b 2 12

Sim, ele é o mesmo de uma placa com espessura c desprezível!

Passo 2

No entanto, nos foi pedido o momento de inércia em relação à um eixo especial. Como esse eixo é paralelo ao eixo do qual conhecemos o momento de inércia relacionado, podemos usar o teorema dos eixos paralelos.

Vamos usar uma imagem para nos ajudar no cálculo da distância d entre os eixos.

Usando Pitágoras, temos:

d 2 = a 2 2 + b 2 2

Finalmente, usando o teorema, temos:

I = I 0 + M d 2

I = M a 2 + b 2 12 + M   a 2 2 + b 2 2

Substituindo os valores:

I = 0,172 3,5 2 + 8,4 2 12 + 0,172 1,75 2 + 4,2 2

I ≅ 4,74   k g . c m 2

Resposta

I ≅ 4,74   k g . c m 2

Exercício Resolvido #3

UFRJ-P2-2014.1-M03

Uma esfera oca e rígida de massa M e raio R tem momento de inércia I c m = 2 / 3 M R 2 relativo a um eixo que passa pelo seu centro de massa. Relativamente a um eixo que tangencia a periferia da esfera e é paralelo ao eixo que passa pelo centro de massa, o momento de inércia da esfera é

  1. I c m
  2. 1 / 3 M R 2
  3. 5 / 3 M R 2
  4. 7 / 10 M R 2
  5. 2 I c m

Passo 1

Para achar esse momento de inércia vamos usar o teorema dos eixos paralelos. Faremos isso porque o enunciado nos deu o valor do momento de inércia dessa esfera em relação a um eixo e pediu em relação a um eixo paralelo.

Passo 2

Vamos ter

I ' = I c m + M d 2

A distância entre os eixos vai ser o raio da esfera.

I ' = 2 3 M R 2 + M R 2

I ' = 5 3 M R 2

Resposta

Letra C

Exercícios de Livros Relacionados

Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto
Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k
Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.