Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Momento de inércia de uma partícula

Ver Todos os Exercícios

Teoria

E aí?! Você está no Responde Aí! E aqui a gente te ensina rapidão tudo pra passar na prova.

Quando você se deparar com problemas de movimento de rotação, uma hora ou outra vai precisar calcular o momento de inércia de uma partícula

Pra calcular o momento de inércia de uma partícula a gente usa uma fórmula bem simples:

í

onde í é a massa da partícula, é a distância entre a partícula e o eixo de rotação, e é o momento de inércia da partícula

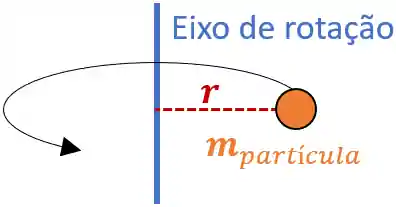
Partícula em eixo de rotação
Partícula em eixo de rotação

Mas o que é Momento de Inércia?

Quando a gente trabalha com problemas de movimento de rotação sempre existe um eixo de rotação que é fixo durante o movimento dos outros corpos.

O momento de inércia é a dificuldade que um corpo tem de rotacionar.

Vamos fazer um experimento:

Pegue uma folha solta aí qualquer, de preferência uma A4 ou perto desse tamanho. Se você tentar segurar a folha por uma aresta dela ela vai cair né? Isso porque a rigidez à rotação dela é baixa, vamos agora aumentar a rigidez dessa parada ai. Enrola a folha fazendo um cilindro, segura de novo pela ponta da folha e vê o que acontece.

AHÁ, a folha não dobra mais. Você não mudou a massa está vendo? Só mudou a forma aumentando a rigidez à rotação da folhinha de papel. Você está mudando o momento de inércia!

Momento de Inércia de um sistema de partículas:

Um sistema de partícula acontece quando temos ao menos duas partículas se movimentando ao redor de um mesmo eixo de rotação.

Quando temos um sistema de partículas podemos calcular o momento de inércia do sistema apenas somando o momento de inércia de todas as partículas:

Exemplo

Observe o sistema de duas partículas abaixo e calcule o momento de inércia de cada partícula, e o momento de inércia do sistema.

Dados: , , ,

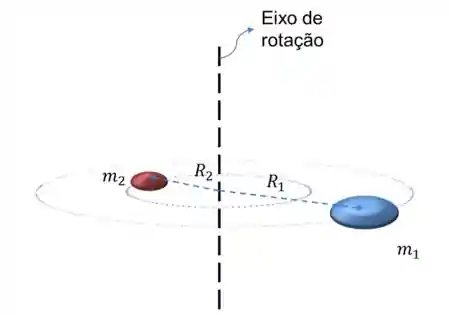
Sistema de partículas em rotação
Sistema de partículas em rotação

Passo 1: Primeiro vamos calcular o momento de inércia da partícula 1

Vamos aplicar a fórmula:

E aplicamos os valores:

Passo 2: E agora a gente calcula o momento de inércia da partícula 2:

Passo 3: E pra finalizar, a gente calcula o momento de inércia do sistema somando o momento de inércia de todas as partículas:

Prontinho! Viu como é de boas?! Agora que tal dar uma olhada nessa videoaula sobre momento de inércia de uma partícula:

Mas o que é Momento de Inércia?

Momento de Inércia de um sistema de partículas:

Exercícios Resolvidos

Exercício Resolvido #1

Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 288-44

As massas e coordenadas de quatro partículas são as seguintes:

50   g ,   x = 2,0   c m ,   y = 2,0   c m

25   g ,   x = 0 ,   y = 4,0   c m

25   g ,   x = - 3,0   c m ,   y = - 3,0   c m

30   g ,   x = - 2,0   c m ,   y = 4,0   c m

Quais são os momentos de inércia desse conjunto em relação ao eixos (a) x , (b) y e (c) z ? (d) Suponha que as respostas de (a) e (b) sejam A e B , respectivamente. Nesse caso, qual é a resposta de (c) em termos de A e B ?

Passo 1

Sabemos que:

I = ∑ I p a r t í c u l a = ∑ i 4 m i r i 2

Ou seja, vamos fazer para cada partícula:

  • Descobrir a distância até o eixo desejado
  • Elevar essa distância ao quadrado
  • Multiplicar pela massa da partícula

E depois iremos somar todos os resultados para obter o momento de inércia do conjunto em relação ao eixo.

Se desenharmos as posições dessas partículas, teremos:

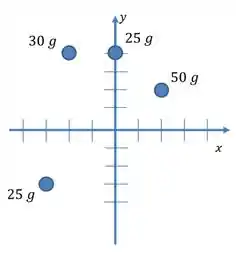
Vamos começar desenhando a distância de cada uma das partículas até o eixo x

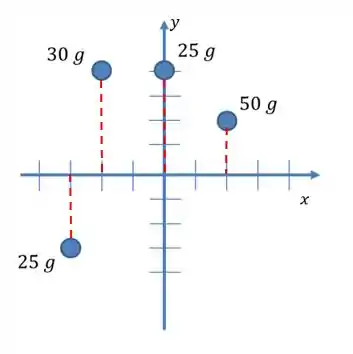
Assim o momento de inércia em relação a esse eixo será:

I x = 0,05   .   0,02 2 + 0,025   .   0,04 2 + 0,025   .   0,03 2 + 0,03   .   0,04 2

I x = 0,0001305   k g . m 2 → I x = 1,305   .   10 - 4   k g . m 2

Passo 2

Fazendo o mesmo pro eixo y :

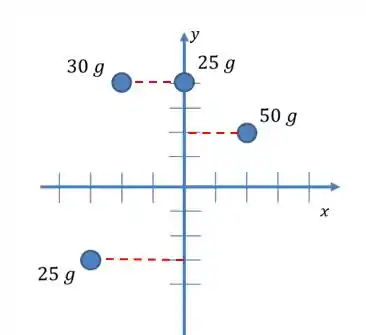
Repare que a massa de 25 g de cima está exatamente sobre o eixo y , o que significa que a sua distância até o eixo y é nula!

I y = 0,05   .   0,02 2 + 0,025   .   0 2 + 0,025   .   0,03 2 + 0,03   .   0,02 2

A segunda massa nessa equação aqui de cima tá exatamente sobre o eixo y , beleza? Isso faz com que a sua distância até o eixo y seja nula!

I y = 0,0000545   k g . m 2 → I y = 0,545   .   10 - 4   k g . m 2

Passo 3

Já para o eixo z , temos que usar o teorema de Pitágoras para achar a distância do ponto ao eixo:

d z = d x 2 + d y 2

Realizando o mesmo método:

I z = 0,05   .   ( 0,02 2 + 0,02 2 ) + 0,025   .   ( 0 2 + 0,04 2 ) + 0,03   .   0,02 2 + 0,04 2 +   0,025   .   0,03 2 + 0,03 2

I z = 0,000185 → I z = 1,85   .   10 - 4   k g . m 2

Outro jeito que a gente pode escrever é

d z 2 = d x 2 + d y 2

Ou seja

I z = ∑ m i d z i 2 = ∑ m i d x i 2 + d y i 2

E podemos dividir esse negócio em dois somatórios

I z = ∑ m i d x i 2 + ∑ m i d y i 2

Reconhece esses caras? Eles são I x e I y !!! :o

I z = I x + I y → I z = 1,305   .   10 - 4 + 0,545   .   10 - 4

I z = 1,85   .   10 - 4   k g . m 2

Resposta

  1. I x = 1,3   .   10 - 4   k g . m 2
  2. I y = 0,55   .   10 - 4   k g . m 2
  3. I z = 1,85   .   10 - 4   k g . m 2
  4. I z = I x + I y

Exercício Resolvido #2

UFRJ-P2-2012.1-ME4

Considere um corpo rígido constituído por: hastes finas, rígidas, de massa desprezível e de comprimento l e um conjunto de nove massas iguais a m (que podem ser consideradas puntiformes) conforme a figura abaixo. O momento de inércia I A B desse conjunto em torno do eixo A B é dado por:

  1. I A B = 0  
  2. I A B = m l 2
  3. I A B = 6 m l 2
  4. I A B = 9 m l 2
  5. I A B = m 4 l 2 + 4 2 l 2

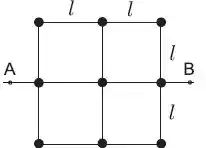
Passo 1

O momento de inércia do conjunto é a soma dos momentos de inércia de cada objeto do conjunto.

O momento de inércia de uma partícula em relação ao eixo depende da massa da partícula e da distância da partícula ao eixo. Lembra da fórmula?

I = m r 2

Onde r é a distância da partícula até o eixo.

Passo 2

Vamos ter 3 partículas no eixo, então seu momento de inércia é zero. Enquanto vamos ter 6 partículas a uma distância l do eixo todas com massa m então o momento de inércia I A B vai ser

I A B = 6 ⋅ m l 2 + 3 ⋅ 0 = 6 m l 2

Resposta

Letra C

Exercício Resolvido #3

USP-P3-2014-2 - a,b,c.

Considere um sistema de cinco objetos puntiformes dispostos em um plano de acordo com a figura a seguir. Cada um dos quatro objetos periféricos possui massa igual a m , enquanto que o quinto, localizado na origem do sistema de coordenadas indicado na figura, tem massa 2 m . Eles são unidos por hastes rígidas e de massas desprezíveis.

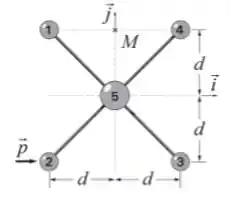
a ) Calcule o momento de inércia do sistema em relação ao eixo passando pelos objetos 2 e 3 .

b ) Calcule o momento de inércia do sistema em relação ao eixo perpendicular ao plano da figura e passando pela origem.

c ) Calcule o momento de inércia do sistema em relação ao eixo perpendicular ao plano da figura e passando pelo ponto M indicado na figura.

Passo 1

a )

O momento de inércia do sistema pode ser encontrado da seguinte forma:

I = m 1 r 1 2 + m 2 r 2 2 + m 3 r 3 2 + m 4 r 4 2 + m 5 r 5 2

I = m r 1 2 + m r 2 2 + m r 3 2 + m r 4 2 + 2 m r 5 2

Botando m em evidência

I = m r 1 2 + r 2 2 + r 3 2 + r 4 2 + 2 r 5 2

Como o eixo de rotação está passando pelos objetos 2 e 3, temos que as distâncias até o eixo de rotação serão:

r 2 = r 3 = 0

r 1 = r 4 = 2 d

r 5 = d

Logo:

I 23 = m 2 d 2 + 0 + 0 + 2 d 2 + 2 d 2

I 23 = 10 m d 2

Passo 2

b )

Temos agora o eixo passando perpendicularmente ao objeto 5. Neste caso, as distâncias dos objetos 1 ao 4 serão os comprimentos das hastes. Então os vetores posições serão agora:

r 1 = r 2 = r 3 = r 4 = d 2

r 5 = 0

I 5 = m 4 d 2 2

I 5 = 8 m d 2

Passo 3

c )

Com o eixo passando pelo ponto M , teremos as seguintes distâncias:

r 1 = r 4 = r 5 = d

Para calcular as distâncias das partículas 2 e 3 ao eixo, podemos atentar para o triângulo azul abaixo:

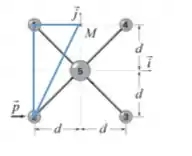
A distância r 2 (que é igual a r 3 ) é dada pela hipotenusa do triângulo! Logo, temos:

r 2 2 = d 2 + 2 d 2 = 5 d 2 → r 2 = r 3 = 5 d

Continuando, teremos:

I M = m d 2 + 5 d 2 + 5 d 2 + d 2 + 2 d 2 = 14 m d 2

Resposta

a )   I 23 = 10 m d 2

b ) I 5 = 8 m d 2

c ) I M = 14 m d 2

Exercícios de Livros Relacionados

1. O centro de massa do haltere da FIGURA Q12.1 encontra-se no ponto a, b ou c? Explique.
Uma viga de 40k g e 5,0m de comprimento é sustentada, sem estar fixada, pelas duas pilastras mostradas na FIGURA P12.64. Um garoto de 20k g começa a caminhar ao longo da viga. Quão próximo ele pode ch
Integrando diretamente, calcule o momento de inércia de uma haste delgada de Massa M e comprimento L em torno de um eixo localizado a uma distância d de uma das extremidades. Confirme se sua resposta
Uma viga rígida com 3,0m de comprimento e massa de 100k g é apoiada em cada extremidade. Um estudante de 80k g encontra-se em pé a 2,0m do suporte 1. Que valor de força cada suporte exerce sobre a vig
Para o sistema de quatro partículas da figura 9-45, (a) determine o momento de inércia I x em relação ao eixo x que passa por m 2 e m 3 e (b) determine o momento de inércia I y em relação ao eixo y qu