Exercícios de Cálculo do Momento de Inércia em Corpos Extensos - Lista de Exercícios Resolvida
Questão 1
Mostre que o momento de inércia de um cilindro de massa e raio em relação ao eixo central é igual ao momento de inércia de um aro fino de massa e raio em relação ao eixo central. Mostre que o momento de inércia de um corpo qualquer de massa em relação à qualquer eixo é igual ao momento de inércia de um aro equivalente em torno do mesmo eixo, se o aro tiver a mesma massa e um raio dado por
O raio do aro equivalente é chamado de raio de giração do corpo.
Ver solução completaQuestão 2
O momento de inércia de uma barra reta homogênea em relação a um eixo perpendicular a ela e ao plano do papel e que passa pelo seu centro de massa vale . Num dado instante a barra é dobrada em torno de seu ponto médio de maneira que assuma a forma de um “V” cujo ângulo de abertura é . O momento de inércia da barra dobrada em relação ao mesmo eixo é
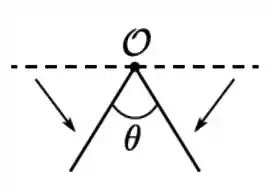
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 3
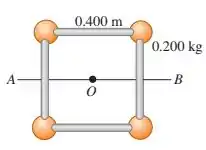
Quatro pequenas esferas, todas consideradas massas puntiformes com massa de , estão dispostas nos vértices de um quadrado de lado igual a e conectadas por hastes leves (figura abaixo). Calcule o momento de inércia do sistema em relação a um eixo:
a) perpendicular ao quadrado e passando pelo seu centro (um eixo passando pelo ponto 0 na figura);
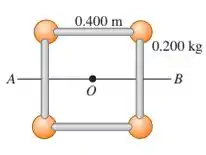
Questão 4
Quatro pequenas esferas, todas consideradas massas puntiformes com massa de , estão dispostas nos vértices de um quadrado de lado igual a e conectadas por hastes leves (figura abaixo). Calcule o momento de inércia do sistema em relação a um eixo:
b) cortando ao meio dois lados opostos do quadrado (um eixo ao longo da linha AB indicada na figura);
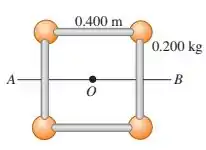
Questão 5
Duas barra idênticas de mesma massa e comprimento são usadas para desenhar um objeto com a forma de letra . O objeto pode girar em torno dos eixos indicados pela linha tracejada na figura. Para os momentos de inércia a , relacionados com a rotação em torno ao eixo indicado, pode-se afirmar que:
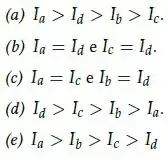
Questão 6
Um balanço de parque é formado por uma barra cilíndrica de massa , raio , e comprimento , preso por fios de massa desprezível a um eixo fixo superior, paralelo ao eixo da barra cilíndrica, conforme a figura ao lado. A barra pode girar em torno desse eixo fixo. O centro da barra está a uma distância d do eixo. O momento de inércia da barra com relação ao eixo fixo vale:
Questão 7
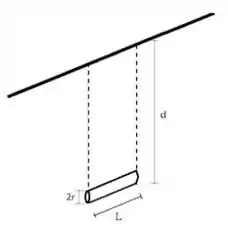
Uma barra homogênea de comprimento e massa está presa em uma de suas extremidades a uma parede vertical, conforme a figura ao lado. A barra gira sem atrito ao redor do ponto , sendo abandonada na posição horizontal com velocidade inicial nula. O momento de inércia da barra em relação ao ponto é e a aceleração da gravidade local é . No instante em que a barra faz um ângulo com a vertical, a aceleração angular da barra é:
Questão 8
Considere o carrossel, da figura abaixo, como um disco de massa e raio . As barras horizontais são finas, têm massa e comprimento . As barras verticais também são finas, possuem massa e altura . O eixo central é constituido por um cilindro de massa e raio desprezíveis.

Dados:
Disco: ;
Haste: ;
;
(a) Calcule o momento de inércia desse carrossel em relação ao eixo central vertical (CM).
Ver solução completaQuestão 9
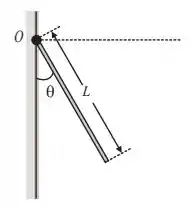
Um pêndulo (vide figura) possui uma haste de comprimento e massa . Em sua extremidade inferior há um disco de massa e raio , cuja borda está colada na extremidade inferior da haste. A extremidade superior da haste pode girar em torno de um eixo sem atrito que permite o conjunto haste-disco oscilar.
Haste: ; Disco:
a) Obtenha uma expressão literal para o momento de inércia do conjunto haste-disco em relação à extremidade superior da haste.
Ver solução completaQuestão 10
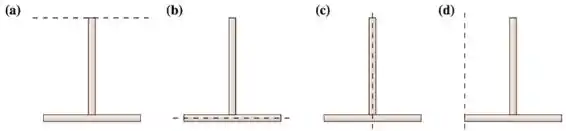
Três objetos em “T” são feitos, cada um, com duas hastes idênticas, de mesma massa e mesmo comprimento. Eles giram com velocidade angular constante em torno dos eixos tracejados. Sabendo que todas as configurações têm a mesma energia cinética de rotação, o que se pode dizer sobre o módulo da velocidade angular em cada caso?
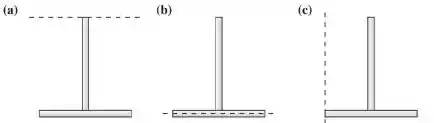
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 11
Considere uma partícula de massa girando em torno de um ponto com velocidade angular e raio , um anel de raio e massa total girando em torno de seu eixo de simetria com a mesma velocidade angular, e um disco de massa total girando em torno de seu eixo de simetria com a mesma velocidade angular. Se os momentos de inércia da partícula, do anel e do disco forem iguais a e , respectivamente, assinale a resposta certa:
A.
B.
C. .
D.
E.
Ver solução completaQuestão 12
Uma barra extremamente leve medindo 1,0 m tem uma massa de 2,0 kg conectada a uma de suas extremidades e uma massa de 3,0 kg conectada à outra extremidade. O sistema gira em torno de um eixo fixo, perpendicular ao comprimento da barra e localizado a 30 cm da extremidade onde se encontra a massa de 3,0 kg. Considerando as massas como partículas, qual é o momento de inércia desse sistema em relação ao eixo de rotação?
a) 10,2
b) 125
c) 1,20
d) 0.50
e) 1,25
Ver solução completaQuestão 14
É possível distinguir entre um ovo cru e um cozido, girando-os sobre uma mesa. Explique como. Além disso, se você parar com os dedos um ovo cru que esteja girando e o soltar rapidamente, ele voltará a girar. Por quê?
Ver solução completaQuestão 15
Se dois discos de mesma massa e espessura são feitos de metais de densidades
diferentes, qual deles possuirá a maior inércia rotacional em torno do seu eixo de
simetria?
Ver solução completaQuestão 16
(Capítulo 9.1 – Exercício 60) Uma roda de amolar está inicialmente em repouso. Um torque externo constante de é aplicado sobre a roda durante , imprimindo à pedra uma rapidez angular de . O torque externo é então retirado, e a roda atinge o repouso depois. Determine (a) o momento de inércia da roda e (b) o torque causado pelo atrito, suposto constante.
Ver solução completaQuestão 17
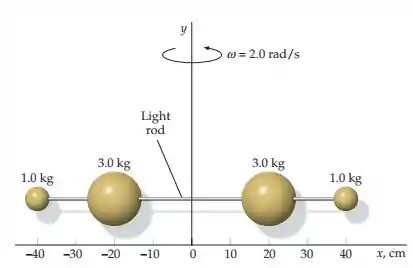
(Capítulo 9.1 – Exercício 64) As partículas da figura estão ligadas por uma barra muito leve. Elas giram em torno do eixo a . (a) Determine a rapidez de cada partícula e utilize esses valores para calcular a energia cinética do sistema diretamente a partir de . (b) Determine o momento de inérica em relação ao eixo , calcule a energia cinética a partir de e compare seu resultado com o resultado da parte (a).
Questão 18
. Complete a seguinte afirmação: "O centro de massa é ...” escolhendo uma:
“o único ponto em um objeto no qual a força gravitacional atua.";
“o ponto de um objeto que se move sob a ação de uma força externa como se toda a massa
do objeto estivesse concentrada nele.";
“o ponto no centro geométrico de um objeto.";
“a região de um objeto onde a densidade tem o maior valor.";
“a região de um objeto onde a maior parte da massa está situada.";
Ver solução completaQuestão 19
Quatro pequenas esferas, todas consideradas massas puntiformes com massa de , estão dispostas nos vértices de um quadrado de lado igual a e conectadas por hastes leves (figura abaixo). Calcule o momento de inércia do sistema em relação a um eixo:
c) passando pelo centro da esfera superior da esquerda e pelo centro da esfera inferior da direita e através do ponto 0.
Questão 20
Disco fino e uniforme de massa e raio está montado sobre um eixo passando através de seu centro e perpendicular ao plano do disco. Determine o momento de inércia sobre dois eixos paralelos e perpendiculares ao plano do disco
- O próprio eixo passando pelo centro do disco.
- Um eixo passando nas bordas do disco.
Questão 21
Uma ruela padrão tem um raio interno e um raio externo de . A ruela tem espessura de . A densidade da liga metálica da ruela é Calcule o momento de inércia da ruela para um eixo que passa pelo seu centro e perpendicular ao plano dela.
Ver solução completaQuestão 22
(Cap 10.2 – Ex. 7) A roda da Fig. 10-27 tem oito raios de igualmente espaçados, está montada em um eixo fixo e gira a . Você deseja atirar uma flecha de de comprimento paralelamente ao eixo da roda sem atingir um dos raios. Suponha que a flecha e os raios são muito finos.
(a) Qual é a menor velocidade que a flecha deve ter?
(b) O ponto entre o eixo e a borda da roda por onde a flecha passa faz alguma diferença? Caso a resposta seja afirmativa, para que ponto você deve mirar?
Ver solução completaQuestão 23
(Cap 10.6 – Ex. 33) Calcule o momento de inércia de uma roda que possui uma energia cinética de quando gira a .
Ver solução completaQuestão 24
(Cap 10 – Ex 39) Na Fig. 10-36, duas partículas, ambas de massa , estão ligadas uma à outra, e a um eixo de rotação em , por duas barras finas, ambas de comprimento e massa . O conjunto gira em orno do eixo de rotação com velocidade angular . Em relação a , quais são
a) o momento de inérica do conjunto e
b) a energia cinética do conjunto?
Ver solução completaQuestão 25
Durante uma exibição, Evgeni Plushenko, patinador artístico russo e três vezes campeão do mundo, está girando em torno de um eixo vertical com os braços estendidos horizontalmente. Em um certo instante, quando ele se aproxima os dois braços do estômago, pode-se afirmar que:


Questão 26
12) Calcule o momento de inércia de uma roda que tem uma energia de quando gira a
Ver solução completaQuestão 27
13) Calcule o momento de inércia de uma régua de um metro, com uma massa de , em relação a um eixo perpendicular à régua na marca de . Trate a régua como uma barra fina.
Ver solução completaQuestão 28
14) Dois cilindros uniformes, ambos girando em torno do eixo central (longitudinal) com uma velocidade angular de , têm a mesma massa de e raios diferentes. Qual é a energia cinética de rotação (a) do cilindro menor, de raio
Ver solução completaQuestão 29
Os corpos estão ligados por barras muito leves cujos momentos de inércia podem ser desprezados. O sistema gira em torno do eixo y com velocidade angular.
c. Determine o momento de inércia do sistema em torno do eixo y e calcule a energia cinética do sistema utilizando a relação .

Questão 30
47. Durante uma exibição, um patinador está girando em torno de um eixo vertical com os braços estendidos horizontalmente. Em um certo instante, quando ele aproxima os dois braços do estômago, pode-se afirmar que:

(a) O seu momento de inércia diminui, o seu momento angular permanece constante e sua energia mecânica aumenta.
(b) O seu momento de inércia, momento angular e energia cinética diminuem.
(c) O seu momento angular permanece constante e sua energia cinética diminui.
(d) O seu momento de inércia aumenta, e seu momento angular e energia mecânica permanecem constantes.
(e) O seu momento de inércia, momento angular e energia cinética aumentam.
Ver solução completaQuestão 31
Um objeto composto por uma haste muito fina de massa e comprimento e um aro fino de raio e massa é livre para girar em torno dos eixos e. A origem do eixo de coordenadas está no centro do aro e no centro da haste. Nos cálculos utilize 3 números significativos.
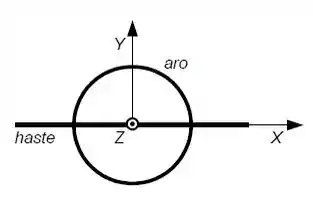
a) Calcule o momento de inércia do objeto em torno dos eixos e . Em torno de qual eixo é mais fácil girar o objeto?
b) O objeto do item anterior é acelerado em torno do eixo . Partindo do repouso, no tempo ele alcança uma velocidade angular . Determine neste instante de tempo quais são os módulos das acelerações tangencial e radial na extremidade da haste.
Ver solução completaQuestão 32
Seja um corpo na forma de um quadrado de lado composto por hastes finas com massas indicadas na figura. Na figura está também indicado o sistema de coordenadas a ser utilizado. O corpo pode girar livremente sem atrito em torno do eixo e encontra-se em repouso na posição indicada.
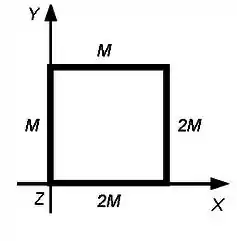
(a) Determine o momento de inércia rotacional do corpo em torno do eixo em função dos dados do problema.
Ver solução completaQuestão 33
Uma barra homogênea de comprimento é emendada a outra de mesmo comprimento, também homogênea, mas com o dobro da massa, conforme a figura.
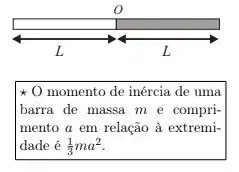
O símbolo na figura marca o ponto da emenda. Quando e representam as massas das barras, o momento de inércia e a distância do centro de massa do sistema em relação ao ponto de emenda valem, respectivamente:
Questão 34
Dois discos uniformes de mesma espessura têm a mesma massa, mas são feitos de materiais de diferentes densidades. O disco com menor momento de inércia em relação a um eixo perpendicular ao plano do disco passando pelo centro é
(A) o disco feito do material mais denso
(B) o disco feito do material menos denso
(C) nenhum dos dois, os momentos de inércia são iguais
(D) o disco com maior velocidade angular
(E) o disco com maior torque
Ver solução completa