Colisões com Rotação
Teoria
Vamos aprender aqui um tipo de questão um pouco mais complexa, que, apesar de ser parecido com o tipo relacionado lá em Dinâmica de Translação, tem suas particularidades.
Se liga nesse exemplo:
Uma barra de massa e tamanho está em repouso sobre uma mesa sem atrito, presa nessa mesa pelo seu centro de massa. Aproxima-se de uma de suas extremidades uma bolinha de massa com velocidade . Se a colisão é elástica, qual é a velocidade angular da barra após a colisão?
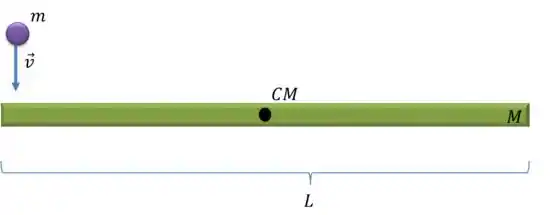
Já vimos como resolver esse problema quando a colisão é inelástica, mas, e agora?
Vamos com calma, sem desespero.
Primeiro de tudo, temos que reconhecer que essa questão vai usar conservação do momento angular, já que não há torques externos agindo, mas aqui uma diferença na situação após o choque, se liga:
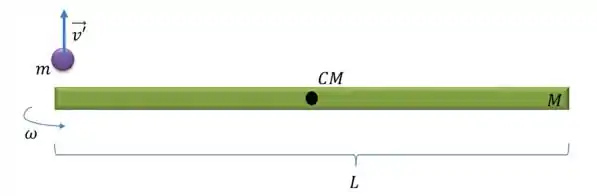
Para a situação inicial, temos a mesma coisa:
No entanto, depois do choque, temos:
Aí vem a dúvida: como achar o valor de ? Vamos ter que usar um outro conceito de conservação: o da conservação da energia.
Vamos lá então, sem choramingar:
Antes do choque, temos só a bolinha se movendo:
Beleza, a energia do sistema depois do choque vêm tanto do movimento de retorno da bolinha quanto a rotação da barra, então:
Se liga que o valor usado para a energia de rotação da barra depende da nossa incógnita principal, .
Igualando as energias, temos o valor de (em função de ):
Agora podemos voltar à nossa conservação do momento angular. Como eles tem o mesmo sentido, vou fazer as equações somente com o módulo:
Deixando o membro com raiz sozinho em um dos lados e elevando ao quadrado:
Esse tipo de questão fica meio grande quando fazemos toda ela literal, mas normalmente os professores colocam valores bonitos para as contas darem certo no final. Esse tipo de questão requer muita prática, principalmente para você não errar conta na hora da prova. Então, não deixe de fazer os exercícios!
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 322-55
Uma barra fina uniforme com de comprimento e massa pode girar em um plano horizontal em torno de um eixo vertical passando pelo centro. A barra está em repouso quando uma bala de é disparada, no plano de rotação, em direção a uma das suas extremidades. Vista de cima, a trajetória da bala faz um ângulo de com a haste (Fig. 11-52). Se a bala se aloja na barra e a velocidade angular da barra é imediatamente após a colisão, qual é a velocidade da bala imediatamente antes do impacto?
Passo 1
Se analisarmos o sistema como um todo, vemos que não há torque externo agindo no mesmo, portanto, podemos usar a conservação do momento angular!
Como a barra está em repouso antes do impacto, o momento angular inicial se dá somente pelo movimento da bala:
Substituindo os valores:
Passo 2
Após o impacto nós temos uma barra com uma bala acoplada girando com velocidade angular .
Para encontrar o momento de inércia do sistema:
E o momento angular do sistema após o impacto é dado por:
Passo 3
Agora é só igualar os momentos angulares antes e depois do impacto!
Resposta
Exercício Resolvido #2
UFRJ-P2-2012.1-Questão Discursiva n°2
Uma haste homogênea e uniforme, de espessura desprezível, com massa e comprimento , pode girar sem atrito em torno de um pino que passa por uma de suas extremidades, como mostra a figura. O movimento da haste fica restrito a um plano vertical e o módulo da aceleração local da gravidade é igual a .
- Sabendo-se que o momento de inércia da haste em relação a um eixo perpendicular à mesma, e que passe pelo seu centro de massa é igual a , calcule o momento de inércia da haste em relação ao eixo de rotação que passa pelo pino.
- Se a haste for liberada na posição horizontal, a partir do repouso, determine sua velocidade angular no instante que passa pela posição vertical.
- Calcule o momento de inércia do sistema haste-corpo após a colisão em relação ao pino.
- Qual é a velocidade angular do sistema haste-corpo de massa , imediatamente após a colisão?
Ainda em relação à situação descrita no ítem anterior, considere que ao passar pela vertical, a exterminadade livre da haste se choque com um pequeno corpo de massa , originalmente em repouso. O corpo de massa adere à haste, e o conjunto continua em movimento de rotação em torno do pino.
Passo 1
a)
Para achar o momento de inércia em relação ao eixo que ele pediu basta fazer o teorema dos eixos paralelos
Nesse caso a distancia entre os eixos vai ser
Então
Passo 2
b)
Estamos em uma situação onde a energia mecânica da barra vai ser conservada, isso porque o atrito está sendo desconsiderado.
Inicialmente vamos ter
Lembra que quando fazemos a energia potencial pegamos a altura do centro de massa ?
Então
Passo 3
A energia mecânica final vai ser
Onde
E
Usamos aqui o momento de inécia em relação ao eixo de rotação
Assim
Passo 4
Igualando as energias vamos ter
Passo 5
c)
O momento de inércia do sistema vai ser
Já sabemos o momento de inércia da barra, e o corpo é uma partícula
Com
O momento de inércia do sistema fica
Passo 6
d)
Repare que temos uma colisão onde o torque externo é zero. Então o momento angular se conserva. Vamos nos preocupar com o momento angular porque temos corpos girando. Vamos ter, antes da colisão
Passo 7
Vamos chamar de a velocidade angular após a colisão. Então, depois da colisão
Passo 8
Igualando os momentos angulares
Resposta
Exercício Resolvido #3
UFRJ-P2-2012.2-Q2
Uma barra delgada homogênea e uniforme, de massa e comprimento , é articulada num pino , que passa por uma de suas extremidades, e pode girar sem atrito num plano vertical. Liberada a partir do repouso na posição horizontal, a barra sofre uma colisão elástica com um pêndulo ao passar pela posição vertical, como representa a massa de dimensões desprezíveis presa à extremidade da haste. O pêndulo também pode oscilar em torno do pino, sem atrito, no mesmo plano vertical que a barra. Sabe-se que o pêndulo encontrava-se em repouso antes da colisão com a barra, e que o momento de inércia da barra em relação ao eixo perpenducular ao plano vertical e que passa pelo pino é
- Determine a velocidade angular da barra, , imediatamente antes da colisão com o pêndulo.
- Quais das seguintes grandezas: o momento linear e o momento angular em relação a são conservadas na colisão? Justifique a sua resposta.
- Determine a velocidade angular da barra, , imediatamente após a colisão.
- Determine o valor da razão para que a barra permaneça em repouso depois da colisão.
Passo 1
a)
Para acharmos a velocidade angular antes da colisão, vamos usar a conservação de energia mecânica. Isso é possível porque não temos forças dissipativas, tipo o atrito, atuando.
Inicialmente vamos ter
Lembra que quando fazemos a energia potencial pegamos a altura do centro de massa ?
Então
Passo 2
A energia mecânica final vai ser
Onde
E
Usamos aqui o momento de inécia em relação ao eixo de rotação
Assim
Passo 3
Igualando as energias vamos ter
Passo 4
b)
Não teremos forças externas nem torques externos atuando, isso nos diz que tanto o momento linear quanto o momento angular em relaçã a será conservado.
Passo 5
c)
Vamos nos preocupar com o momento angular porque temos corpos girando. Vamos ter, antes da colisão
Passo 6
Vamos chamar de a velocidade angular da barra após a colisão e a velocidade angular do pendulo após a colisão. Então, depois da colisão
Precisamos então achar o momento de inércia do corpo e o corpo é uma partícula, então
Com
O momento angular do sistema após a colisão fica
Passo 7
Igualando os momento angulares antes e depois da colisão, vamos deixar a velocidade angular inicial como só para facilitar as contas
Só essa equação não resolve o nosso problema.
Passo 8
O enunciado disse que a colisão é elástica, isso nos diz que a energia cinética vai ser conservada durante a colisão.
A energia cinética antes da colisão vai ser
A energia cinética depois da colisão fica
Igualando as energias
Passo 9
Temoso sistema
Que lindo esse menino né? SQN. Esse sistema é bem complicado de resolver, então vamos a “matemágica”
Vamos começar dividindo as duas equações por
Vamos ter, pela primeira equação
Na segunda equação
Substituindo a subtração vamos ter
Encontrando
Passo 10
Vamos substituir o valor de encontrado no fim do passo na primeira equação
Agora substituímos o valor de
Passo 11
d)
A barra permanecer em repouso significa que a velocidade angular depois da colisão é zero
É o mesmo que
Resposta
- Não teremos forças externas nem torques externos atuando, isso nos diz que tanto o momento linear quanto o momento angular em relaçã a será conservado.
Exercício Resolvido #4
USP-P3-2015-Questão 9
Uma pessoa está com os braços abertos sobre uma plataforma giratória (com atrito desprezível no giro) presa ao chão. Nessa posição, o momento de inércia da pessoa com a plataforma é em relação ao eixo de rotação da plataforma. Um disco uniforme de massa raio é lançado com velocidade e velocidade angular conforme a figura. O disco é agarrado pela mão e para de girar, ficando seu centro a uma distância do centro do sistema pessoa-plataforma, na altura dos braços. Determine:
a) O vetor momento angular do disco em relação ao seu centro de massa antes de ser agarrado.
b) O vetor momento angular total do disco em relação ao centro do sistema pessoa-plataforma na altura dos braços, antes de ser agarrado.
c) O momento de inércia do conjunto plataforma-pessoa-disco em relação ao eixo de rotação da plataforma, após o disco ser agarrado.
d) Qual o vetor velocidade angular do conjunto plataforma-pessoa-disco após o disco ser agarrado pela mão? Girará o conjunto no sentido horário ou anti-horário?
Passo 1
a)
Pra calcular o momento angular é tranquilinho, só utilizar a relação:
Como, nesse caso , teremos:
Substituindo os valores...
Passo 2
b)
É bom tomar bastante cuidado com os vetores aqui!!
O momento angular nesse caso será dado pela soma do momento angular do centro de massa com a definição, é uma espécie de Teorema dos Eixos Paralelos para o momento angular, saca só:
Decompondo vetorialmente, teremos:
Daí...
O que nos dá como resposta...
Passo 3
c)
Sabemos que o será a soma dos momentos de inércia, logo:
Como o disco gira em torno de um eixo distante, pelo Teorema dos Eixos Paralelos, teremos:
Passo 4
d)
Não haverá torque pois a força resultante do sistema é o peso, que passa pelo eixo de rotação, logo o momento angular se conservará. Dessa forma, escrevemos:
Isolando o :
Que é o sentido anti-horário.
Resposta
a)
b)
c)
d)