Giroscópios
Teoria
Os giroscópios são instrumentos que conservam o momento angular, o seu eixo de rotação se mantém sempre na mesma direção desde que não aja nenhuma força que o perturbe. Já parou pra pensar como a agulha da bússola aponta sempre para a mesma direção? É graças ao giroscópio!
A gente preparou um vídeo completíssimo sobre giroscópio, nele você aprende tudo o que você precisa saber sobre esse assunto para arrasar na sua prova de física! Se liga só 👇
📢 Clique para ver mais:
Celulares com Giroscópio
Talvez já tenha se deparado com o nome “giroscópio” quando você estava pesquisando pra comprar seu celular novo! Afinal essa é uma funcionalidade de muitos celulares atualmente.
No celular o giroscópio funciona como um sensor que detecta a velocidade angular do aparelho. Dessa forma se você gira seu smartfone o giroscópio consegue detectar, assim o seu aparelho sabe se você esta apontando ele pra cima ou pra baixo!
Maneiro, não é?! 😍
Momento Angular e Torque em um Giroscópio
No funcionamento do giroscópio temos a força peso e a velocidade angular, como mostrado na figura abaixo:
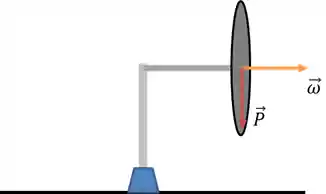
O momento angular
Já o torque
Movimento de Precessão
A precessão é a mudança do eixo de rotação de um objeto. No nosso caso temos o torque como um vetor perpendicular ao vetor do momento angular, isso significa que o torque vai alterar somente a direção do momento angular! E assim nós temos o nosso movimento de precessão.
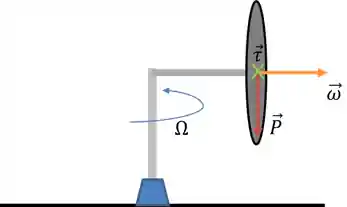
Como podemos observar na figura acima, o movimento de precessão será a rotação do eixo que segura a roda em torno do eixo vertical. Usamos normalmente a letra Ω para a velocidade angular desse movimento, que pode ser calculado por:
Agora vamos praticar com exercícios?
Momento Angular e Torque em um Giroscópio
Movimento de Precessão
Exercícios Resolvidos
Exercício Resolvido #1
USP-P3-2015-1
Um giroscópio está montado sobre um suporte vertical conforme a figura. Assinale a afirmativa incorreta:
a) Numa vista superior, o giroscópio girará no sentido anti-horário.
b) O vetor momento angular total do giroscópio em relação ao centro O é constante ao longo do tempo.
c) O torque é proporcional à massa do girocópio.
d)O movimento de um eixo de rotação ao redor de um eixo fixo devido a um torque externo é chamado de precessão.
e) Quanto mais rápido a roda do giroscópio girarem torno de seu eixo, menor será a velocidade angular de precessão.
Passo 1
a)
Fazendo a regra da mão direita, veremos que a roda girará no sentido anti-horário. A velocidade de precessão é uma velocidade que “persegue” a velocidade angular , logo ela girará no sentido anti-horário sim.
Passo 2
b)
O torque é perpendicular ao momento angular, desta forma o seu módulo não muda, apenas a direção. Logo a resposta está errada, pois o vetor não é constante e sim apenas o módulo.
Passo 3
c)
Sim!!
O torque é dado por . E como sabemos o momento de inércia depende da massa, logo o torque também.
Passo 4
d)
Verdade! Esse é justamente o conceito de precessão, uma característica dos giroscópios e também da Terra.
Passo 5
e)
A velocidade angular de precessão pode ser calculada por:
Nesse caso, quando o aumenta o diminui.
Afirmativa correta.
Resposta
b) O vetor momento angular total do giroscópio em relação ao centro O é constante ao longo do tempo.
Exercício Resolvido #2
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 324-69
Um certo giroscópio é formado por um disco uniforme com de raio montado no centro de um eixo de de comprimento e massa desprezível. O eixo está na posição horizontal, apoiado em uma das extremidades. Se o disco está girando em torno do eixo a , qual é a taxa de precessão?
Passo 1
Aqui nós temos um giroscópio clássico, portanto, está de acordo com essa imagem:
Aprendemos que a taxa de precessão pode ser calculada da seguinte maneira:
Mas sabemos que o momento de inércia de um disco é dado por:
Substituindo, temos:
O enunciado nos deu todos esses valores, então:
Resposta
Exercício Resolvido #3
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 324-68
Um pião gira a em torno de um eixo que faz um ângulo de com a vertical. A massa do pião é , e seu momento de inércia em relação ao eixo central é e seu centro de massa está a do ponto de apoio. Se a rotação é no sentido horário quando vista de cima, quais são (a) a taxa de precessão e (b) o sentido da precessão quando o pião é visto de cima?
Passo 1
a) Esse é um problema cheio de informação, vamos desenhar pra facilitar as coisas.
Da imagem, se tentarmos fazer uma analogia com o giroscópio clássico, temos que a distância do ao centro de rotação é análogo ao tamanho do braço que segurava a roda no giroscópio clássico. Portanto:
E agora temos todas as informações necessárias para encontrar o valor da taxa de precessão:
Passo 2
b) Já para este item, temos que analisar a direção do torque, pela regra da mão direita, temos:
Como o torque está saindo do papel e ele é responsável pelo movimento de precessão, se olharmos o movimento de cima, a velocidade angular da precessão estará no sentido horário.
Vale notar que o mesmo acontece se tomássemos os de inclinação para a esquerda!
Resposta
- Sentido horário