Conservação do Momento Angular
Produzido por Ludovic BeghinTeoria
O momento angular mede a quantidade de movimento de um corpo em rotação, ele é a relação entre a inércia e a velocidade angular! Agora… sabia que em determinadas situações o momento angular se conserva?!
Quando Temos a Conservação do Momento Angular?
O momento angular se conserva desde que não haja torques externos agindo no sistema. Assim:
📢 Clique para ver mais:
- Conservação do Momento Angular: Exercícios Resolvidos
- Tabela do Momento de Inércia
- Colisões com Rotação
Como Provar que um Sistema Conserva o Momento Angular
Vamos fazer um exemplo! Imagina que um menino gira uma bolinha de massa
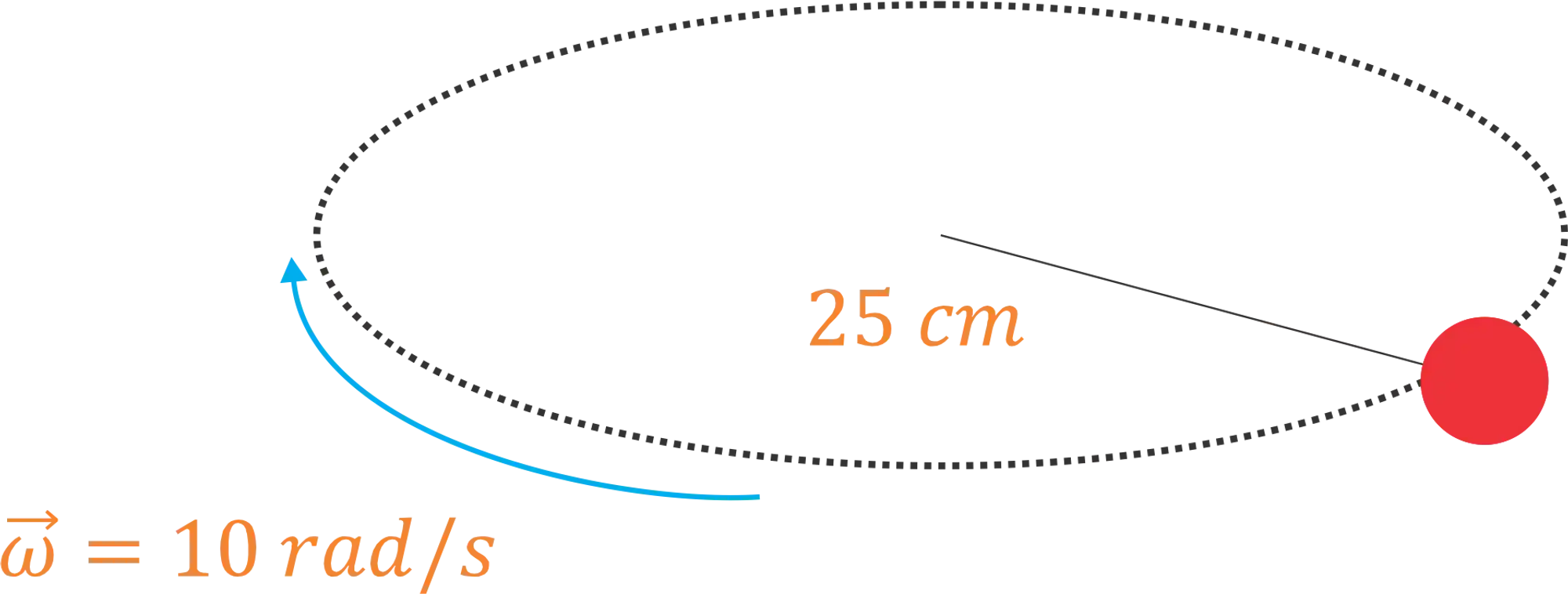
Se a trajetória aumentar, como na figura abaixo o que vai acontecer com a velocidade? Se não há torques externos no sistema é possível haver conservação de momento angular?
Se a gente analisar a bolinha em si, só teremos a força peso atuando na direção vertical e a força de tração na corda apontando para o centro do movimento.
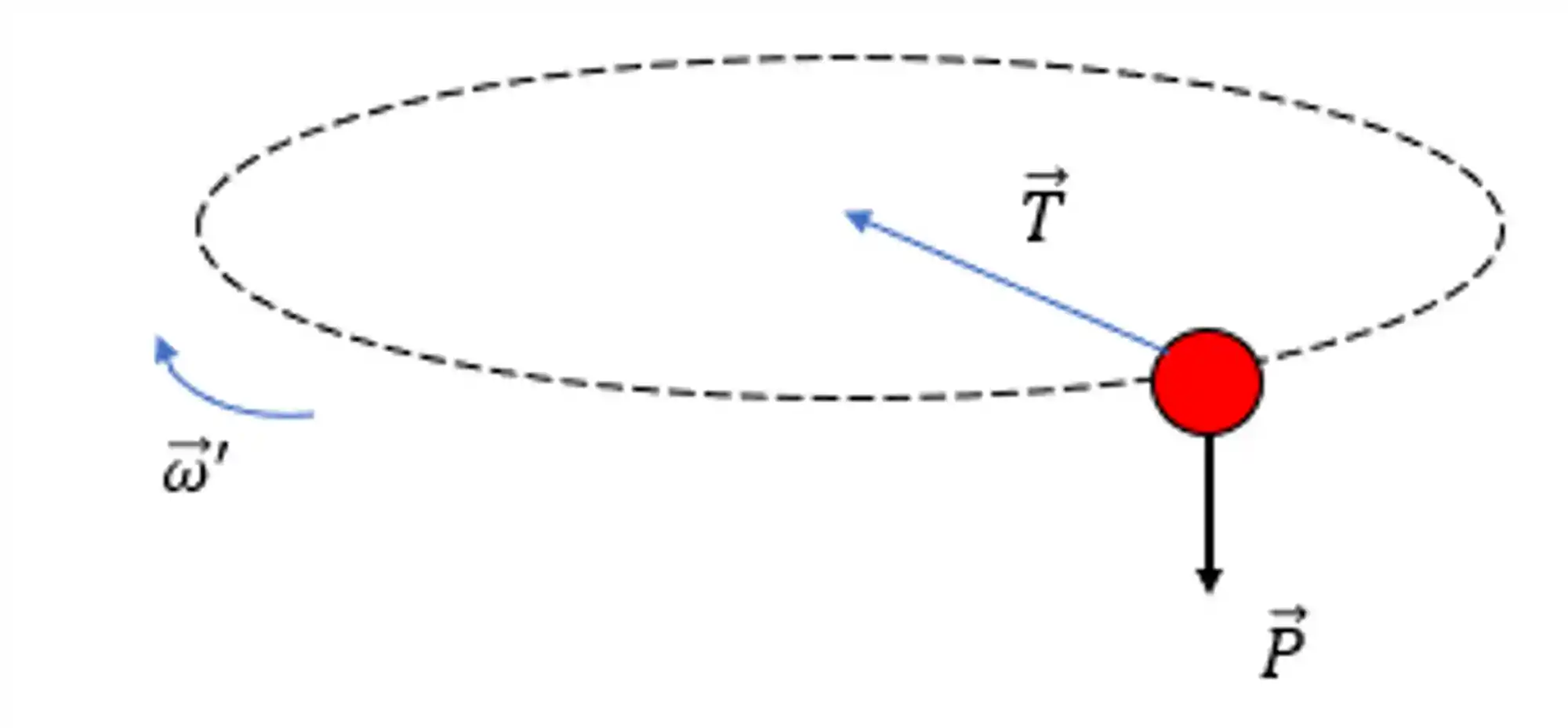
A tração, por apontar na direção do raio do movimento circular, não gera torque. A força peso até é suficiente pra gerar um torque, mas esse torque não é na direção do nosso movimento, então na nossa trajetória o momento angular se conserva.
Em corpos pontuais a gente costuma usar o momento angular da seguinte forma:
Mas como a gente tá interessado em encontrar a velocidade angular do corpo, usaremos:
Sendo assim:
O momento de inércia de um corpo pontual é dado por:
A gente pode ver pelas figuras que o menino aumentou a trajetória, aumentando assim o momento de inércia. No primeiro momento temos:
Depois do aumento no raio da trajetória, temos:
Então usando a conservação do momento angular e isolando a velocidade angular, temos:
Substituindo:
Ou seja, nesse caso o momento de inércia não se conserva!
Você também pode conferir esse conteúdo em vídeo:
Vamos praticar com exercícios?
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ-PF-2015.1-ME3
Considere as afirmativas abaixo:
(I) Em uma colisão inelástica, o momento linear do sistema nunca é conservado.
(II) A velocidade do centro de massa de um sistema de partículas é sempre constante.
(III) Forças internas nunca alteram o momento linear total de um sistema de partículas.
(IV) O momento linear e o momento angular de um sistema de partículas sempre se conservam sob a ação de um par de forças externas de mesmo módulo, direção e sentidos opostos.
São verdadeiras apenas as afirmativas:
(a) I
(b) III
(c) II e IV
(d) II e III
(e) III e IV
Passo 1
Vamos ver as afirmativas uma por uma!
Afirmativa (I):
O fato da colisão ser inelástica não muda nada! Pro momento linear ser conservado, basta não ter forças externas atuando no sistema, seja a colisão elástica, inelástica ou nenhuma das duas.
Então a afirmativa é falsa.
Passo 2
Afirmativa (II):
Essa propriedade só é válida num caso particular, se a soma das forças externas atuando no sistema é nula!
A afirmativa é falsa.
Passo 3
Afirmativa (III):
A gente sempre fala que o momento linear do sistema se conserva se não tem forças externas atuando né? Isso porque são elas que alteram o momento linear do sistema.
A gente nunca fala das forças internas porque elas não mexem no momento linear, elas justamente são as forças que não são internas.
Portanto, a afirmativa é verdadeira.
Passo 4
Afirmativa (IV):
Que nem a gente já viu algumas vezes nessa questão, pro momento linear se conservar a soma das forças externas tem que ser zero. E a soma de duas forças externas de mesmo módulo, direção e sentidos opostos dá zero, certo? Então nesse caso o momento linear se conserva.
Passo 5
Agora vamos dar uma olhada no momento angular.
Pra ele se conservar, a soma dos torques externos (em relação a um certo eixo) é que tem que dar zero. E o torque realizado por 2 forças externas de mesmo módulo, direção e sentidos opostos pode muito bem dar diferente de zero!
Saca:

As forças e realizam torque em relação ao eixo passando pelo centro de massa da barra!
Então num caso como esse o momento angular não se conserva.
Portanto, a alternativa é falsa.
Resposta
Alternativa (b)
Exercício Resolvido #2
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 321-44
O rotor de um motor elétrico tem um momento de inércia em relação ao eixo central. O motor é usado para mudar a orientação da sonda espacial no qual está montado. O eixo do motor coincide com o eixo central da sonda; a sonda possui um momento de inércia em relação a esse eixo. Calcule o número de revoluções do rotor necessárias para fazer a sonda girar em torno do eixo central.
Passo 1
Como não há torques externos ao sistema, podemos usar conservação do momento angular.
Se multiplicarmos ambos os lados por e integrarmos:
Assim como na translação, essas integrais valem a distância percorrida, nesse caso, a distância percorrida é angular.
Substituindo os valores:
Sabemos que cada revolução é igual a , então
Resposta
Exercício Resolvido #3
UFRJ-PF-2014.2-ME3
Uma nave espacial isolada tem um eixo de simetria em relação ao qual seu momento de inércia é . A nave gira em torno desse eixo com velocidade angular constante de módulo . Aciona-se um mecanismo interno da nave que reduz seu tamanho, sem perder sua simetria relativa ao eixo de rotação, de modo que ao final seu momento de inércia relativo a esse eixo se reduz a . A velocidade angular final da nave no tamanho final é dada por
(a)
(b)
(c)
(d)
(e)
Passo 1
Vejamos, a questão envolve rotação e os dados são momento de inércia e velocidade angular. Está pedindo pra gente usar a fórmula do momento angular
Por isso, vamos assumir que não há torque externo sendo realizado em relação ao eixo de rotação, assim o momento angular se conserva. (Sim, é chato ficar assumindo coisas mas quando o enunciado não tá claro é o jeito!)
Passo 2
Pronto! Isso significa que
Resposta
Alternativa (a)
Exercício Resolvido #4
UNICAMP-P3-2014.B
Um homem com os braços junto ao corpo está em cima de uma cadeira giratória que gira sem atrito. Quando o homem estende os braços:
a) A velocidade angular da cadeira aumenta
b) A velocidade angular da cadeira continua a mesma
c) O momento de inércia do homem diminui
d) A energia cinética do sistema aumenta
e) O momento angular do sistema continua o mesmo
Passo 1
Bem, lembrando dá fórmula:
Vemos que a aceleração angular é diretamente influenciada pelo momento de inércia. Ou seja, visto que estender os braços não altera o torque, podemos encarar ele como constante. Então, se aumentarmos o momento de inércia, a aceleração angular irá diminuir para manter o torque constante, e vice versa.
Como a aceleração é intimamente ligada a velocidade. Podemos afirmar a mesma coisa. Se o momento de inércia aumenta, a velocidade cai e vice versa.
Certo, já deu para perceber que só precisamos analisar o momento de inércia para acertar a questão!
A fórmula do momento de inércia é:
Ou seja, depende quadraticamente da distância ao centro de massa. Então, como ao abrir os braços o homem aumenta a distância até o centro de massa, ele também estará aumentando o momento de inércia.
Então nossa conclusão é que o momento de inércia aumenta e consequentemente a velocidade e aceleração angulares iram diminuir.
Vamos então analisar as alternativas.
Alternativa : A velocidade angular da cadeira aumenta.
Errado. Já concluímos que a velocidade angular diminui.
Alternativa : A velocidade angular da cadeira continua a mesma.
Errado. Como já dissemos, a velocidade angular diminui.
Alternativa : O momento de inércia do homem diminui.
Errado. Já vimos que o momento de inércia aumenta.
Alternativa : A energia cinética do sistema aumenta.
Errado. Se a velocidade angular diminui, a energia cinética também diminui já que possui a fórmula:
Alternativa : O momento angular do sistema continua o mesmo.
Vamos verificar. Analisando a fórmula:
Ou seja, para termos variação do momento angular, é preciso ter um torque externo. E não tem torque externo ao sistema cadeira+homem. Logo essa alternativa está correta. O momento angular se conserva.
Resposta
Alternativa
Exercício Resolvido #5
UFRJ-P2-2012.2-ME8
Um disco uniforme é montado em um eixo horizontal de massa desprezível, em torno do qual pode girar livremente, como mostra o diagrama. O momento de inércia do disco em relação ao eixo é . O disco está inicialmente girando com velocidade angular ; vide figura. O disco é movimento horizontalmente para esquerda até que sua face entre em contato com um disco idêntico, que está inicialmente em repouso. Depois de um pequeno intervalo de tempo, os dois discos acoplam-se e passa a girar juntos com uma velocidade angular final . Em relação às grandezas: velocidade angular final, energia cinética de rotação e momento angular do sistema, pode-se afirmar que ao final do processo de acoplamento:
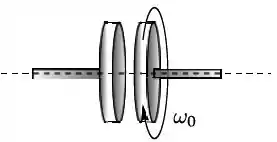
- , não é conservada, não é conservado;
- , é conservada, não é conservado;
- , é conservada, não é conservado;
- , não é conservada, é conservado;
- , é conservada, é conservado;
Passo 1
Como não temos torques externos o momento angular do sistema se conserva
Vamos ter
E
Igualando vamos ter
Passo 2
Já vimos que o momento angular é conservado vamos agora calcular a energia cinética inicial e a final, que neste caso é apenas de rotação
E
Como
Vamos ter
Então a energia cinética não se conserva.
Resposta
Letra D