Conservação de Energia
Produzido por Ludovic BeghinTeoria
Fala aí! Seja muito bem vindo ao Responde Aí! Bora bater um papo sobre Conservação de Energia?!
Princípio da Conservação de Energia
O Princípio da Conservação da Energia diz que: "A energia pode ser transformada ou transferida, mas nunca criada ou destruída".
Isso quer dizer que ao longo do tempo a energia total de um sistema será constante! Vamos ver como isso funciona?
Conservação de Energia Mecânica
A energia mecânica é a soma de todas as energias que atuam em um corpo. Para nós aqui, é plausível considerar que em um corpo atuam apenas a Energia Cinética e a Energia Potencial, então a energia mecânica será a soma dessas duas formas de energia:
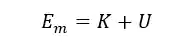
Onde:
é a energia mecânica; é a energia cinética; é a energia potencial.
Quando falamos em conservação de energia mecânica estamos querendo dizer que a energia mecânica de um corpo é a mesma em todos os instantes e em qualquer posição.
Em outras palavras, a energia de um corpo pode sofrer transformações de energia cinética para energia potencial ou o vice-versa , porém a energia mecânica total se conserva.
Dessa forma:
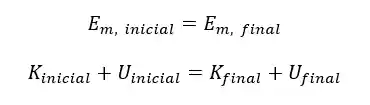
-Beleza, mas como eu posso calcular a energia cinética e a energia potencial?!
Excelente pergunta! Vamos ver isso agora 👇
Energia Cinética
A energia cinética é a energia associada ao movimento do corpo, ela pode ser calculada a partir da seguinte fórmula:
Onde:
é a energia cinética, medida em joules ; é a massa do objeto, em quilograma ; - é
a velocidade do objeto, em ;
Energia Potencial
A energia potencial que aparece na fórmula da energia mecânica ela é uma contribuição tanto da Energia Potencial Gravitacional, quanto da Energia Potencial Elástica.
A energia potencial gravitacional é a energia associada a posição do objeto em relação a um nível de referência, e sua fórmula é a seguinte:
é a energia potencial gravitacional, em Joule ; é a massa do objeto, em quilograma ; é a altura que o objeto está em relação ao nível de referência, em metros ; é a aceleração da gravidade, em .
Já a energia potencial elástica é a energia associada as propriedades elásticas de uma mola, e sua fórmula é a seguinte:
Onde:
é a energia potencial elástica, em Joule ; é a constante elástica da mola, expressa em ; é a deformação da mola, o quanto a mola foi comprimida ou esticada, expressa em .
Exemplo: Uma maçã presa em uma macieira a
A primeira coisa que precisamos ver são as forças que atuam no corpo!
Nesse caso, apenas a força peso esta atuando sobre a maça, e como a força peso é uma força conservativa, a conservação da energia mecânica pode ser aplicada.
Aplicando a conservação de energia teremos:
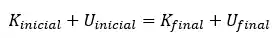
Agora, vamos analisar com calma a situação.
Inicialmente a maça está presa na árvore, ou seja, está parada, não tem movimento, então
Assim, a equação da conservação fica:
Agora, podemos utilizar a fórmula da energia cinética e potencial:
Agora, podemos isolar a velocidade final, pois é ela que queremos calcular:
Agora, precisamos substituir os valores. A altura inicial é dita no problema,
E solucionamos o problema!!
Conservação de Energia Mecânica: Vídeo Aula
Agora, pra encerrar com chave de ouro, confere essa vídeo aula super completa sobre a conservação de energia mecânica! 👇
Agora que você tá sabendo tudo sobre conservação de energia, bora praticar com exercícios?
Conservação de Energia Mecânica: Vídeo Aula
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Uma massa está suspensa no campo gravitacional por uma mola de constante elástica presa ao teto. Efeitos de atrito são desprezíveis e observa-se que o sistema oscila verticalmente em torno de sua posição de equilíbrio. A opção correta é:
- A energia mecânica do sistema não se conserva, pois alem da força gravitacional sobre a massa há, adicionalmente, a força elástica exercida pela mola.
- A energia mecânica do sistema se conserva, se considerarmos que esta é a soma das energias cinética e energia potencial gravitacional da massa.
- A energia mecânica do sistema se conserva, se considerarmos que esta é a soma das energias cinéticas e energia potencial elástica da mola.
- A energia potencial total, dada como a soma das contribuições de energia potencial gravitacional e energia potencial elástica, é conservada.
- A energia mecânica do sistema se conserva, se considerarmos que esta é a soma das energias cinética e das energias potencial gravitacional e potencial elástica da mola.
Passo 1
As forças que atuam no corpo são o peso e a força elástica, que são forças conservativas
Isso nos diz que a energia mecânica se conserva, já que só temos forças conservativas atuando. Além disso, a energia mecânica, como temos a força gravitacional agindo e uma força elástica será:
Resposta
Letra E
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 1 , 9º ed. Rio de Janeiro: LTC , 2008, pp 194-Modificado
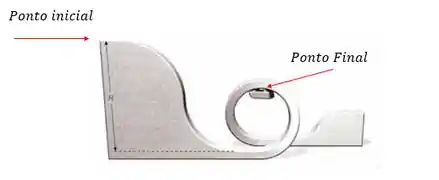
Um pequeno bloco, inicialmente em repouso, é liberado em uma rampa sem atrito a uma altura de . As alturas das elevações ao longo da rampa estão indicadas na figura. Os cumes das elevações são todos iguais, de forma circular, e o bloco não perde contato com o piso em nenhuma das elevações.
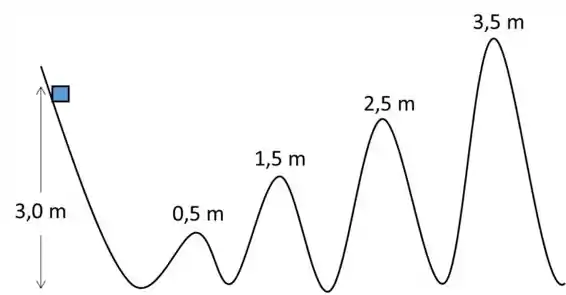
Qual é a primeira elevação que o bloco não consegue superar?
O que acontece com o bloco em seguida?
Passo 1
De acordo com a lei de conservação de energia mecânica, a energia mecânica antes tem que ser igual a energia mecânica depois.
Já que o bloco parte do repouso, ele possui apenas energia potencial. Tendo isso em vista, é impossível que ele alcance uma altura maior que a altura inicial dele ( ), pois caso isso aconteça, a energia mecânica depois será maior que a energia mecânica inicial.
Portanto, o bloco não irá conseguir superar a elevação de .
Passo 2
O bloco irá escalar o ultimo cume até a altura de e depois inverterá a direção do seu movimento e retornará a posição inicial, entrando em movimento oscilatório entre a posição de inicio e a posição de altura do último cume.
Resposta
Ele não ultrapassará o último cume.
Ele retornará a posição inicial.
Exercício Resolvido #3
TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 232 – 38.
Um bloco de desliza sobre uma superfície horizontal sem atrito com uma rapidez de . Após deslizar por uma distância de , o bloco faz uma suave transição para uma rampa sem atrito inclinada de um ângulo de com a horizontal. Qual a distância, ao longo da rampa, que o bloco percorre até atingir momentanaeamente o repouso? ()

Passo 1
É importante saber que não há nenhuma força dissipativa atuando no objeto. O que vai acontecer é que toda a energia cinética que o bloco possui será convertida em energia potencial gravitacional.
Passo 2
Calculando a energia cinética da caixa.
Passo 3
Agora vamos converter essa energia cinética em energia potencial gravitacional
Isolando o temos:
Passo 4
Apesar sabermos a altura que ele subiu na rampa, precisamos saber quanto ele anda ao longo da rampa. Aqui vai entrar uma trigonometria bem tranquila, vou até botar um desenho pra te ajudar. Botei uma caixinha de leite pra ficar mais legal, hahahaha
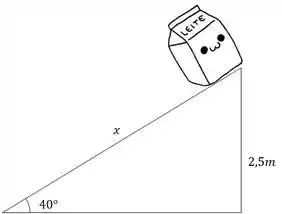
3,9m
Resposta
Exercício Resolvido #4
TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 233 – 47.
Um carrinho de montanha-russa, de , parte do repouso de uma altura acima da base de uma laço de de diâmetro. Se o atrito é desprezível, determine a força para baixo exercida pelos trilhos sobre o carrinho, quando este está no topo do laço, de cabeça para baixo.

Passo 1
O que vai acontecer aqui é o seguinte, o carrinho sai do repouso mas quando chega lá embaixo tem velocidade. Isso acontece por quê a energia mecânica envolvida no sistema se conserva e podemos usar a equação que iguala as energias inicial e final.
No looping o carrinho vai realizar um movimento circular, onde a força resultante é a força centrípeta que aponta para o centro da circunferência.
Usaremos esses dois conceitos pra resolver essa questão, a conservação de energia vai ajudar a gente a encontrar a velocidade no topo do looping e a força centrípeta pra encontrar a força que os trilhos fazem no carrinho.
Passo 2
Vamos pegar o ponto de onde o carrinho parte do repouso e o topo do looping, e fazer aqui a conservação de energia.
No ponto mais alto da montanha a energia mecânica será a inicial, e como não tem velocidade é somente a energia potencial.
No topo do laço, o carrinho terá energia cinética e potencial, nesse caso ele já perdeu alguma altura agora em relação ao chão tem altura de que é o diâmetro da trajetória.
Igualando as energias temos:
Substituindo , , e , temos:
Para descobrir a velocidade no ponto mais alto do laço, vamos usar a fórmula da energia cinética:
Passo 3
Agora que já sabemos a velocidade, podemos calcular a força que os trilhos exercem sobre o carrinho
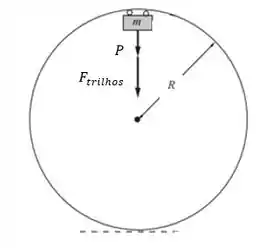
A força peso e a força dos trilhos apontam pra baixo nesse ponto, sendo assim podemos aplicar a segunda lei de newton pra relacionar a força centrípeta com as forças atuantes.
Como , temos:
Sendo assim temos:
Substituindo valores temos:
Resposta
Exercício Resolvido #5
TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 232 – 34.
Uma máquina de Atwood consiste em duas massas, e e uma polia sem massa e sem atrito. Partindo do repouso, a rapidez das duas massas chega ao final de . Neste tempo, a energia cinética do sistema atinge e cada massa terá se deslocado uma distância de . Determine os valores de e .

Passo 1
Como temos no problema duas incógnitas, e , precisamos de duas equações que as relacionem para depois descobri-las:
Passo 2
Vamos começar, relacionando as duas incógnitas, e , à energia cinética que é fornecida quando elas estão com a seguinte velocidade:
Vamos lá!
Passo 3
Como temos duas incógnitas (e ) precisamos de duas equações para montar um sistema.
Para encontrarmos essa nova equação podemos fazer de dois jeitos. Vou mostrar os dois aqui.
A primeira maneira é usando conservação da energia mecânica.
Mas o exercício diz que ambas as massas partem do repouso, então:
Além disso, o enunciado também nos diz que
Para analisarmos as energias potenciais vamos pensar no seguinte: considerando o zero de energia potencial na posição inicial de 2 e sabendo que ambas as massas se deslocam por 6 metros, temos:
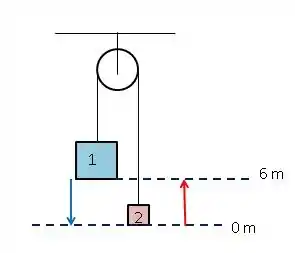
Então:
Assumimos que , então:
E
Como , temos:
Substituindo isso na equação de conservação de energia mecânica:
Mas,
Logo:
Resolvendo isso daí:
Show, temos então essas duas equações:
Resolvendo esse sistemas, encontramos:
Maravilha!! Essa foi a primeira form de acharmos as massas, vou mostrar mais uma.
Passo 4
Vamos usar a segunda lei de Newton, para achar a segunda relação que falta entre e . Sabemos que a aceleração é a mesma para os dois blocos, certo? Só que enquanto um fio sobe, o outro desce. Por isso, consideremos o sentido positivo para cima:
Temos então, o seguinte sisteminha, onde , e são respectivamente o peso do bloco de massa , a força de tração e o peso do bloco de massa .
Somando então as duas equações do nosso sistema, chegamos a:
Só que tem um porém. A questão diz que as massas chegaram a ao final de . Ou seja elas foram aceleradas. Encontramos, o meio de achar a aceleração :
Usando a fórmula da velocidade para o movimento uniformemente acelerado, partindo do repouso temos que:
Voltemos à fórmula anterior:
Tínhamos obtido antes, que:
Opa! Mas que beleza! Só susbtituir agora .
E como:
Resposta
e