Conservação de Energia no Pêndulo
Produzido por Ludovic BeghinTeoria
Esse tipo de exercício não envolve nenhuma teoria nova, ok? Só vamos aplicar o que a gente aprendeu antes, que foi a conservação da energia cinética e da energia potencial gravitacional.
“Mas, pô, se não tem teoria nova, por que eu tenho que aprender?”
O pêndulo é um caso muito comum em algumas questões, cai direto. Daí, já vamos aprendendo uns macetinhos que a gente sempre pode usar para ficar mais fácil!
Energia mecânica no pêndulo
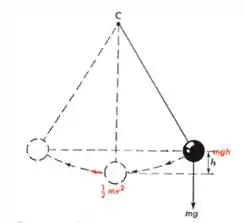
Já percebeu o que sempre ta acontecendo no pêndulo? Sempre que ele chega às extremidades ele para e começa a fazer o movimento inverso, certo? Existem dois pontos super importantes para a gente: quando ele chega as extremidades e quando ele está no ponto mais baixo da trajetória!
Extremidades: Nesse ponto a gente sabe que a velocidade dele é zero, certo? Então nesse ponto toda a energia mecânica dele vai ser a energia potencial gravitacional, pois a energia cinética é nula!
Obs: calma que a gente vai arranjar um macetinho pra esse ai.
Ponto mais baixo: Sempre que pegarmos um pêndulo o macete é adotar esse ponto aqui como sendo , mas por que?
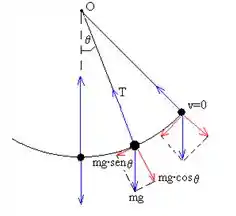
A força peso durante toda a trajetória antes de chegar a esse ponto vai acelerando a bolinha, quando chega nesse ponto a aceleração chega a zero! Assim, a velocidade nesse ponto é máxima, e como adotamos esse ponto como , vamos ter que toda a energia mecânica é a energia cinética.

Lembrando sempre que vamos adotar o ponto mais baixo do pêndulo como sendo !!!
Calculando o h
Se lembra do que a gente tinha deixado pra depois? Não deixamos ele passar não!
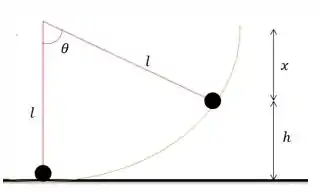
Bom, nós queremos calcular o valor de certo? A gente sabe que faz parte de , ou seja:
Pra descobrir esse vamos ter que usar esse ângulo que a corda faz com a vertical quando a altura é máxima!!! Repara só, vamos usar uma trigonometria aqui!
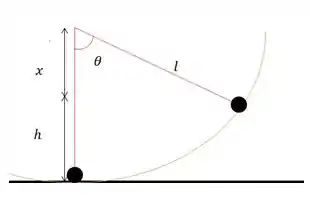
Se nós pegarmos o triângulo formado por e a corda no ponto máximo, vamos conseguir escrever o em função do !
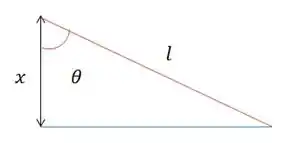
Olhando pra esse triângulo ai e achando o , vamos conseguir escrever tudo em função de e !
Como já tínhamos visto antes
Substituindo o que acabamos de encontrar:
Ângulo máximo
Mas e se ele pedir o ângulo máximo que a corda faz com a vertical? Bom, vamos usar a mesma expressão que achamos antes, só que agora vamos isolar o ângulo!
Dependendo do que o problema pedir você usa a relação certa! Conseguimos relacionar o tamanho da corda, o ângulo e a altura máxima! Quando o problema pedir alguma coisa desse tipo você já sabe o que usar!
Calculando o h
Ângulo máximo
Exercícios Resolvidos
Exercício Resolvido #1
TIPLER,P.- Física para Cientistas e Engenheiros Vol 1,6ª Edição, LTC,2009., pp 233 – 41.
Uma criança de , em um balanço de de comprimento, move-se com uma rapidez de quando o assento do balanço passa pelo seu ponto mais baixo. Qual é o ângulo que o balanço forma com a vertical quando atinge seu ponto mais alto? Despreze a resistência do ar e suponha que a criança não está forçando o balanço.
Passo 1
Vamos considerar que a criança não pega impulso quando está no balanço. O que está acontecendo com ela? Toda a energia que ela tem vai ser convertida em energia potencial gravitacional. Quando você chega no ponto mais alto no balanço, sua velocidade é zero. Vamos considerar aqui o chão como sendo o ponto mais baixo do balanço.
Passo 2
Para começar a questão, vamos calcular a energia total que ele possui. Quando ele passa pelo ponto mais baixo do balanço, sua energia cinética é máxima e ele não possui energia gravitacional, pois .
Passo 3
Assim, no ponto mais alto do balanço, toda a energia mecânica da criança irá se transformar em energia gravitacional, pois , logo, .
Passo 4
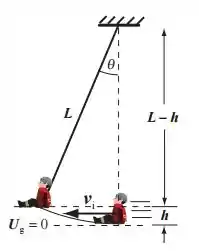
Agora que já sabemos a altura, vamos usa-la para calcular o ângulo que a corda faz no ponto mais alto. Sabendo a altura, conseguiremos descobrir o , pois sabemos a hipotenusa do ângulo, , e o cateto adjacente, .
Resposta
Exercício Resolvido #2
TIPLER, P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 234 – 52.
Um pêndulo de de comprimento, com uma bolinha de , é largado do repouso quando forma um ângulo de com a vertical. Na parte mais baixa da oscilação, a rapidez da bolinha é .
- Quanto vale ?
- Qual é o ângulo que o pêndulo forma com a vertical quando a rapidez da bolinha é ? Este ângulo é igual a ? Explique o porquê da resposta.
Passo 1
A ideia desse exercício é quase a mesma do anterior. Durante a oscilação ele não perde e nem ganha energia mecânica, pois não há nenhuma força dissipativa atuando no pêndulo. O que vai acontecer é que a energia potencial gravitacional do sistema vai ser transformada em energia cinética. Vamos achar as respostas?
Passo 2
Alternativa a)
Vamos usar dois pontos, certo? Vamos chamar de o ponto onde o pêndulo é largado do repouso e o ponto mais baixo da oscilação. Vamos considerar o ponto mais baixo da oscilação como
Calculando a energia mecânica em :
Passo 3
Agora que já sabemos a energia mecânica do sistema, podemos usa-la para achar a energia gravitacional em , já que como o pêndulo estava no repouso, ele não possui velocidade.
Passo 4
Agora que já sabemos a altura, vamos usa-la para calcular o ângulo que a corda faz no ponto mais alto. Sabendo a altura, conseguiremos descobrir o , pois sabemos a hipotenusa do ângulo, , e o cateto adjacente, .
Passo 5
Alternativa b)
O que ta acontecendo agora de diferente? Agora, ele não vai ter só energia cinética ou só energia gravitacional, ele vai ter ambas. Vamos calcular a energia cinética com a velocidade que ele deu e a energia mecânica nós já sabemos, pois ela é igual em todos os pontos!!!
Passo 6
Para calcular o ângulo vamos usar a mesma idéia:
O ângulo não é metade do ângulo inicial, pois esse ângulo é linearmente dependente da energia gravitacional, e essa energia não é linearmente depende da velocidade, por isso que não fica a metade
Resposta
Alternativa a)
Alternativa b)
Exercício Resolvido #3
UFRJ- Física 1-Prova 1- 2015.1-Discursiva n°1
Uma partícula de massa está presa a um fio ideal de comprimento cuja outra extremidade está fixada a um ponto A no teto.
A partícula é largada do repouso quando o fio faz um ângulo com a vertical. Ao passar pelo ponto mais baixo de sua trajetória, o fio se rompe. Utilize o sistema de coordenadas indicado na figura e despreze todas as resistências.
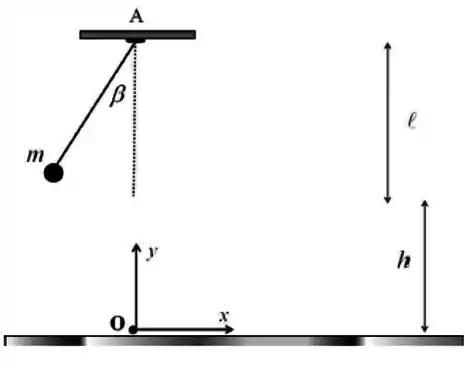
a) Faça um diagrama das forças que atuam sobre a partícula no momento imediatamente anterior ao rompimento do fio.
b) Calcule o vetor velocidade da partícula neste momento, justificando seus cálculos.
c) Calcule o módulo da tensão no fio no instante imediatamente anterior ao seu rompimento.
d) Sendo a altura que a partícula se encontra no momento do rompimento do fio, medida a partir do chão, obtenha a distância horizontal percorrida por ele desde o instante do rompimento do fio até o instante em que ele atinge o chão.
Passo 1
a)
As únicas forças atuando na partícula nesse momento são a força peso e a força de tensão do fio (ou tração, tanto faz). Então o diagrama é:

Passo 2
b)
Queremos a velocidade da partícula logo antes do fio romper, sendo que ela partiu do repouso. Então parece uma boa aplicar a conservação da energia mecânica.
Vejamos, a força peso é conservativa. E a força de tensão é sempre perpendicular ao movimento da partícula, então ela não realiza trabalho. Ou seja, não tem nenhuma força não-conservativa realizando trabalho.
Beleza, podemos aplicar a conservação da energia mecânica! A energia mecânica inicial é igual à energia mecânica final :
Passo 3
Sendo a energia cinética e a energia potencial gravitacional, a equação fica:
A partícula sai do repouso, então .
A energia potencial gravitacional é relativa, então vamos considerar que vai facilitar bastante as nossas contas. Ou seja:
sendo a altura inicial da partícula.
Passo 4
Então só precisamos da altura . Pra isso vamos ter que aplicar uma trigonometriazinha. Dá uma olhada nessa figura:
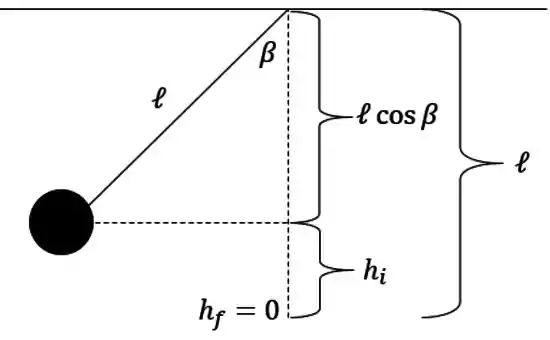
Podemos ver que
Passo 5
Show! Então o módulo da velocidade final que a gente queria é:
Mas ele pediu o vetor velocidade, então temos que ver pra onde ele aponta.
Até logo antes do fio se romper, a partícula está seguindo um movimento circular, então o vetor velocidade é tangente à trajetória. O fio, quando se rompe, está na vertical, então o vetor velocidade está na horizontal, apontando pra direita:
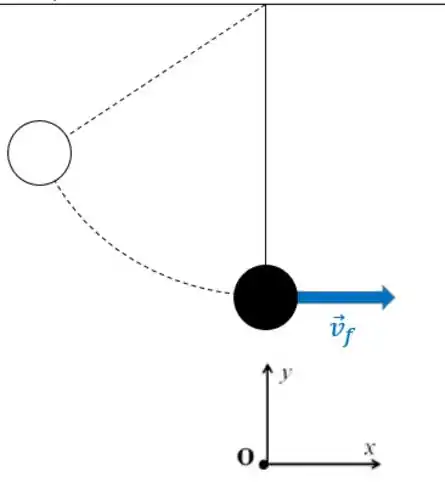
Sendo o vetor unitário do eixo , o vetor velocidade vai ser:
Passo 6
c)
A força resultante atuando na partícula logo antes do fio se romper é:
E pela 2ª lei de Newton,
Logo,
Como a força de tensão aponta pra cima, no sentido do eixo , e a força peso pra baixo, em módulo isso dá:
Passo 7
E essa aceleração a gente consegue achar!
Que nem eu falei antes, logo antes do fio se romper a partícula está seguindo um movimento circular. Na parte mais baixa da trajetória, que é onde o fio se rompe, a sua aceleração é puramente centrípeta!
E a aceleração centrípeta é:
A velocidade a gente já calculou, é , e o raio seria o comprimento do fio , ou seja:
Passo 8
Voltando ao que achamos antes:
Passo 9
d)
Quando o fio se rompe, a tração some então a força resultante sobre a partícula é a força peso:
Então, pela 2ª lei de Newton, vamos ter
Agora a partícula está em queda livre! Mas ela não deixa de ter um movimento horizontal, devido à velocidade que ela tinha quando o fio se rompeu, beleza?
Passo 10
Então o que queremos achar é o alcance da partícula, sabendo que ela foi lançado de uma altura com uma velocidade , e somente sob ação da gravidade.
Vamos separar o movimento em uma componente horizontal e uma vertical, ok?
Passo 11
Começando pela componente horizontal:
A gravidade só age no eixo , no eixo não tem nenhuma força agindo! Ou seja, no eixo a partícula segue um MRU com velocidade .
Então no eixo as equações do movimento são:
Passo 12
Agora vamos ver a componente vertical.
Como já vimos, na vertical o movimento é de queda livre, um MRUV com aceleração . A velocidade da partícula quando o fio se rompe é somente horizontal, no eixo ela é nula.
Então no eixo as equações do movimento são:
Passo 13
Quando a partícula chega no chão, seu deslocamento vertical é nulo. Então digamos que é o tempo no qual a partícula toca o chão. Isso significa que:
Passo 14
No tempo o deslocamento horizontal da partícula é justamente o alcance que queremos achar. Vamos chamar esse alcance de . Então temos
Resposta
a)

b)
c)
d)
Exercício Resolvido #4
TIPLER, Física, Vol 1,6ª Edição, LTC,2009., pp 238 – ex101
Um pêndulo consiste em uma pequena bola de massa presa a um fio de comprimento . A bola é segurada lateralmente, com o fio na horizontal. Então, ela é largada do repouso. No ponto mais baixo da trajetória, o fio se prende a um pequeno prego, a uma distância acima desse ponto. Mostre que deve ser menor do que para que o fio permaneça tenso enquanto a bola completa uma volta inteira em torno do prego.

Passo 1
Bom, vamos lá, pra começar, ele fala que o fio tem que estar tensionado ali, certo? Pra ele estar esticado, tem que ter uma forcinha fazer a bolinha girar, que vai ser a força centrípeta da parada.
Vamos começar a calcular?
Passo 2
Para essa força ser mínima e o fio continuar esticado, a força centrípeta vai ter que ser igual ao peso
Assim temos
Se a velocidade dele for maior, é melhor, que ai a corda fica mais tensionada. Como quanto maior o maior a velocidade, sabemos que vamos encontrar o valor mínimo dele.
Passo 3
Agora que a gente já sabe a velocidade dele quando ele ta rodando, vamos conservar a energia mecânica nos pontos que a gente sabe.
Como consideramos a altura medida a partir do ponto mais baixo (com nesse ponto), então a altura que o pêndulo atinge é . Agora desenvolvendo a equação:
Resposta
Ei, a resposta está no passo a passo :)