Trabalho da Força Gravitacional

Teoria

Fala meu jovem, preparado para aprender de uma vez por todas sobre o trabalho da força gravitacional?

Então vem comigo!

Por definição, o trabalho de uma força é dado pelo produto escalar entre o vetor força e o vetor deslocamento:

Abrindo esse produto escalar temos o seguinte:

Sendo assim, para calcularmos o trabalho de uma força precisamos do módulo do vetor força, do módulo do vetor deslocamento e do cosseno do ângulo que esses dois vetores fazem entre si.

Vamos então aplicar isso para a força gravitacional, ou também conhcida como força peso.

A força gravitacional é um força que atua em todos os corpos, devido a ação da gravidade, sempre na direção vertical e no sentido de cima para baixo. É representada pela letra e seu módulo é o que segue:

Sendo:

a massa do corpo sob o qual a força está atuando, e;
a aceleração da gravidade dada por

Agora vamos imaginar duas situações em que um corpo se desloca em uma distância :

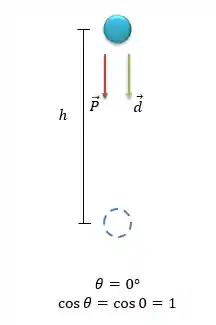
CORPO DESCENDO - Nesse caso, o corpo começa em uma altura e termina em uma altura zero. O vetor deslocamento e a força peso são paralelas, formando um ângulo

Nesse contexto, o trabalho da força gravitacional será o seguinte:

Então, para um corpo descendo, o trabalho da força peso é dado por POSITIVO.

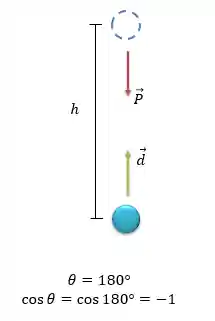
CORPO SUBINDO - Nesse caso o corpo começa em uma altura zero e chega a uma altura . O vetor deslocamento e a força peso são antiparalelas, ou seja, formam um ângulo

Já nesse outro contexto, o trabalho da força gravitacional será o seguinte:

Então, para um corpo subindo, o trabalho da força peso é dado por NEGATIVO.

E é isso que você precisa saber por agora. Vamos fazer exercícios para fixar? 😉

Exercícios Resolvidos

Exercício Resolvido #1

TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 191 – 24.

Uma caixa de é levantada de uma altura de , a partir do repouso, por uma força aplicada vertical de . Encontre o trabalho realizado sobre a caixa pela gravidade

Passo 1

Bom, vamos continuar usando a mesma definição de trabalho

Passo 2

Primeiro, vamos achar a força da gravidade:

Passo 3

Como já sabemos o deslocamente :

Resposta

Exercício Resolvido #2

TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 194 – 58.

Um dos mais potentes guindastes do mundo está em operação na Suiça. Ele pode, lentamente, elevar uma carga de até uma altura de . Qual é o trabalho realizado pelo guinsdaste durante esta tarefa?

Passo 1

Se liga na palavrinha que ele mandou ali: lentamente. Quando ele fala isso, quer dizer que ela subiu muitooooo devagarrrr, ou seja, a gente pode considerar essa força sendo igual a força da gravidade, só que agora vamos considerar que ela tem sentido oposto, né? Ta subindo!

Bom, vamos continuar usando a mesma definição de trabalho

Passo 2

Primeiro, vamos achar a força da gravidade:

Passo 3

Como já sabemos o deslocamente :

Como sabemos que

Resposta

Exercícios de Livros Relacionados

Em cada um dos Problemas de 69 a 72, é fornecida uma ou mais equações para resolver um problema. Em cada um deles, você deve a. Redigir um problema realista para o qual a(s) equação(ções) seja(m) apro

Na Fig. 7-32, uma força horizontal F de módulo 20,0 N é aplicada a um livro de psicologia de 3,00 k g enquanto o livro escorrega por uma distância d = 0,500 m ao longo de uma rampa de incl

(a) Em 1975, o teto do velódromo de Montreal, com um peso de 360k N , foi levantado 10c m para que pudesse ser centralizado. Que trabalho foi realizado sobre o teto pelas forças que o ergueram? (b) Em

Para empurrar um engradado de 25,0k g para cima em um plano inclinado de 25 ° em relação à horizontal, um operário exerce uma força de 209N paralela ao plano inclinado. Quando o engradado percorre 1,5

Um bloco de gelo de 45k g desliza para baixo em um plano inclinado sem atrito de 1,5m de comprimento e 0,91m de altura. Um operário empurra o bloco para cima com uma força paralela ao plano inclinado,