Equilíbrio Estático em Cordas
Produzido por Ludovic BeghinTeoria
Introdução
Já sabemos que uma das condições necessária para o equilíbrio estático é o somatório das forças externas ser zero.
Na maior parte das questões de equilíbrio estático em cordas, basta aplicar essa condição. A diferença aqui é que não vamos aplicar só nos blocos, mas também nos nós das cordas. Também temos que nos atentar a decomposição de vetores que vai estar muito presente.
Equilíbrio Estático em Cordas
Então para as cordas estarem em equilíbrio os seus nós precisam estar em equilíbrio, o melhor jeito da gente entender como isso vai funcionar é na prática, portanto vamos olhar esse probleminha aqui pra entender como funciona.
Imagina que esse bloco está suspenso por essas duas cordas que são fixas às paredes e são inextensíveis, a massa do bloco é . Como encontrar a tensão em cada cabo?
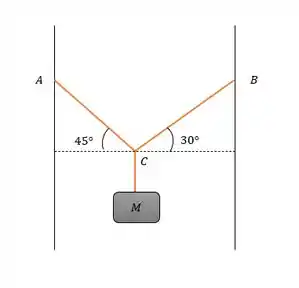
Pra gente encontrar as tensões no cabo vamos precisar respeitar as equações de equilíbrio no nó C e a partir delas tiraremos relações entre as forças.
Já aviso pra vocês que a primeira coisa que a gente tem que fazer sempre é o DCL. Com ele vai ficar muito mais fácil de enxergar as forças atuantes e como decompor elas. Lembrando só que o peso do bloco vai ser dado por:
Vamos de baixo pra cima, começando pelo diagrama de corpo livre do bloco.
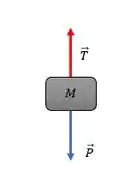
Pelo equilíbrio das forças a gente vê que:
E agora vamos ao DCL da corda, pra analisar o que vai rolar com o nó. Lembrando que transferimos o força de tração no bloco com o sentido invertido pra corda.
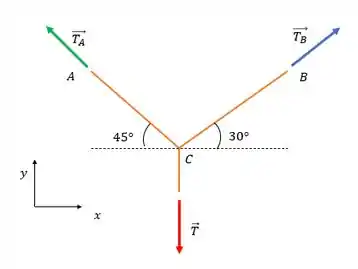
A ideia aqui é decompor as forças nas duas direções e montar um sistema ou encontrar uma relação e substituir numa outra equação, a gente sabe quem é vamos encontrar e . Pra isso vamos primeiro decompor as forças e analisar a situação do nó C.
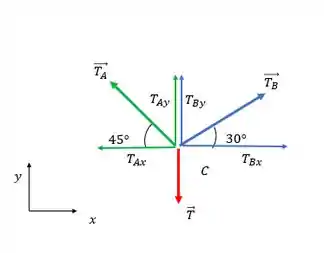
Com a figura a gente pode ver as seguintes decomposições:
Para montar o nosso sistema vamos começar pelo eixo que relaciona e que é o eixo horizontal, e aqui aplicar a equação de equilíbrio no nó C. Você pode arbitrar um sentido, eu vou escolher positivo para a direita e se no fim o sinal der negativo basta indicarmos outro sentido na figura.
Então:
E enfim relacionamos as tensões nos cabos A e B.
Encontrada uma relação entre esses caras a gente pode partir pra outra equação, olhando o que acontece na vertical.
Substituindo os valores encontrados na decomposição das forças temos:
Usando a equação 1, na equação 2 teremos:
Substituindo
E por fim da equação 1 temos:
E aqui é o seguinte, a gente escolheu fazer a horizontal primeiro pela quantidade de incógnitas, mas você poderia ter montado um sistema de equações e resolvido. O importante é entender que vamos aplicar sempre as equações de equilíbrio nos nós e decompor as forças pra encontrar relações entre elas.
Partiu exercícios??
Exercícios Resolvidos
Exercício Resolvido #1
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 12, pp 18-12
O sistema da figura abaixo está em equilíbrio, com a corda do centro exatamente na horizontal. O bloco A pesa 40 N, o bloco B pesa 50 N e o ângulo é 35°.
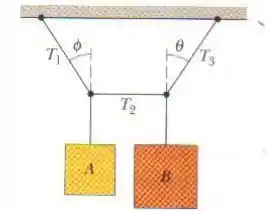
Determine:
- A tensão ,
- A tensão ,
- A tensão ,
- O ângulo .
Passo 1
a)
Analisando as forças no bloco A, montamos o seguinte diagrama:
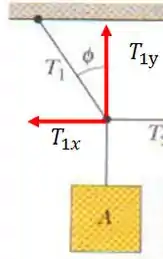
Como o sistema está em equilíbrio:
Passo 2
b)
Montando o diagrama abaixo:
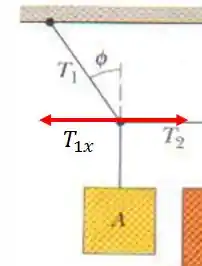
Para o sistema estar em equilíbrio:
Passo 3
c)
Montando o diagrama no ponto que passa:
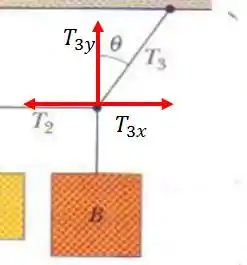
Já a componente de será o peso do bloco que pelo enunciado é , ou seja
é a resultante de e , logo:
Passo 4
d)
Para achar o valor do ângulo , basta calcular a .
Pega uma calculadora aí, e você vai achar que:
Resposta
- 49 N
- 28 N
- 57 N
- 29°
Exercício Resolvido #2
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 12, pp 24-55
Na figura abaixo, uma caçamba de 817 kg está suspensa por um cabo A que está preso no ponto O a dois outros cabos, B e C, que fazem ângulos e com a horizontal. Determine as tensões: Sugestão: Para não ter que resolver um sistema de duas equações com duas icógnitas, defina os eixos da forma mostrada na figura.
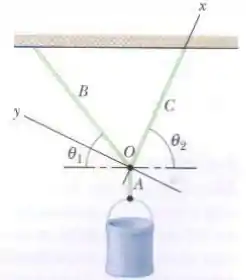
- No cabo A,
- No cabo B,
- No cabo C.
Passo 1
No cabo A, chegamos à conclusão que:
Passo 2
b) Vamos utilizar os eixos conforme sugerido no enunciado:
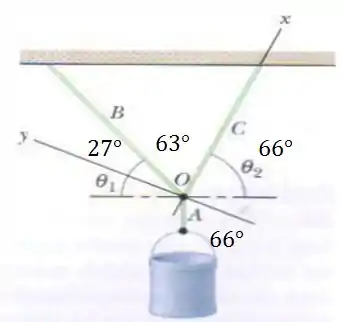
Para o sistema estar em equilíbrio:
Passo 3
Para estar em equilíbrio, o somatório de forças no eixo x também deve ser igual a zero.
Resposta
- 8006 N
- 3654 N
- 5654 N
Exercício Resolvido #3
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 12, pp 24-63
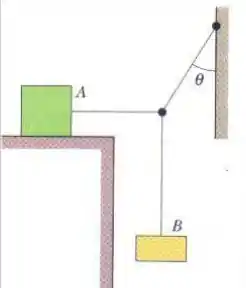
Na figura abaixo, o bloco A, com uma massa de 10 kg, está em repouso, mas escorregaria se o bloco B, que tem uma massa de 5,0 kg, fosse mais pesado.
Se , qual é o coeficiente de atrito estático entre o bloco A e a superfície na qual está apoiado?
Passo 1
Montando primeiramente, o diagrama da questão:
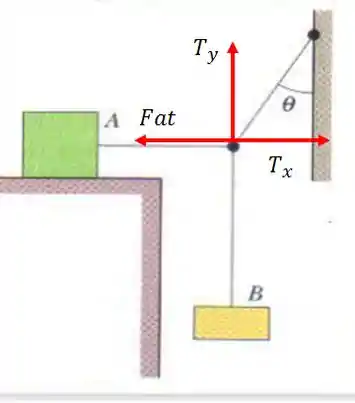
Como trata-se de um equilíbrio estático, podemos montar as equações no eixo x e no eixo y.
Como sabemos o valor do ângulo, podemos deixar em função da tangente do mesmo:
Passo 2
Sabemos que, como o bloco A está na iminência do movimento, a força de atrito é máxima. Logo:
Passo 3
Igualando as duas equações, descobrimos o valor de :