Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Produto Escalar

Ver Todos os Exercícios

Teoria

Fala aí! Bora aprender tudo sobre produto escalar?

O que é um Produto Escalar?

O Produto Escalar é uma operação envolvendo dois vetores que tem como resultado
um escalar.

-Beleza, mas como assim? 😖

Considera dois vetores quaisquer, partindo da mesma origem e formando um ângulo entre eles, assim:

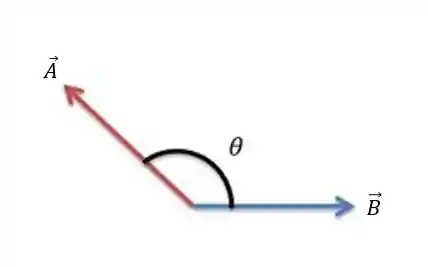
Representação de dois vetores
Representação de dois vetores

Quando fazemos , temos como resultado um número escalar.

Talvez isso possa te soar estranho, afinal, como dois vetores viram um número?!

Mas a gente usa bastante esse conceito no dia a dia! Por exemplo quando calculamos o trabalho de uma força, fazemos o escalar entre o vetor força e o vetor deslocamento!

Beleza, mas vamos ao que interessa…

Como Calcular um Produto Escalar?

Considere dois vetores gerais e :

O produto escalar será:

Ou:

-Tá, mas tá confuso, eu quero um exemplo com números?!

Você quem manda!

Exemplo:

Vamos considerar os vetores e :

O produto escalar entre os vetores e será:

Ué, mas a gente não tem nada em e ! 😖

Não tem problema! É só a gente ignorar ele, ou substituir por zero!

Show, mas e se eu quiser saber qual é o ângulo entre os dois vetores?

Muito simples, você pode fazer:

Já sabemos que:

Calculamos os módulos dos vetores:

Sua multiplicação dá:

Beleza, isolamos o cosseno de :

E agora é só usar a função inversa do cosseno:

E finalmente achamos o ângulo :

Aweee!!

Propriedades do Produto Escalar

Considerando os vetores quaisquer e e o número real , podemos escrever as seguintes propriedades do produto escalar:

  1. Comutativa: ;
  2. Associativa: em que é um número real qualquer;
  3. Distributiva: ;
  4. se e somente se e são vetores perpendiculares.

Produto Escalar - Vídeo Aula

Ficou com alguma dúvida?! Então se liga nessa vídeo aula iradosa sobre produto escalar que o Responde Aí preparou pra você 👇

Agora, vamos praticar com exercícios?!

Como Calcular um Produto Escalar?

Propriedades do Produto Escalar

Produto Escalar - Vídeo Aula

Exercícios Resolvidos

Exercício Resolvido #1

Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 31 – ex1.55

Ache o ângulo entre cada par de vetores:

  1. A → =   - 2,0 î   +   6,0 j                   e                   B → = 2,0 î - 3,0 j  
  2. A → =   3,0 î   +   5,0 j                   e                   B → = 10,0 î + 6,0 j  
  3. A → =   - 4,0 î   +   2,0 j                   e                   B → = 7,0 î + 14,0 j  

Passo 1

Para achar o ângulo entre os vetores vamos usar a fórmula do produto escalar. Como os vetores estão decompostos, vamos ter que calcular o módulo para podermos descobrir o ângulo.

A → ∙ B → = | A → | | B → | c o s ⁡ ( θ )

Onde θ é o ângulo entre os vetores:

Passo 2

Alternativa a)

Calculando o módulo dos vetores:

A → = - 2,0 2 + 6,0 2

B → = 2,0 2 + - 3,0 2

Assim temos:

A → = 2 10

B → = 13

Passo 3

Realizando o produto escalar

A → ∙ B → = | A → | | B → | c o s ⁡ ( θ )

Substituindo os valores temos:

- 2,0 i + 6,0 j 2,0 i - 3,0 j = 2 10 . 13 . c o s ⁡ ( θ )

- 22 2 130 = cos ⁡ θ

cos ⁡ θ = - 0,96

Determinando esse cosseno pela calculadora científica, teremos:

θ ≅ 163,7 °

Passo 4

Alternativa b)

Calculando o módulo dos vetores:

A → = 3,0 2 + 5,0 2

B → = 10 2 + 6,0 2

Assim temos:

A → = 34

B → = 2 √ 34

Passo 5

Realizando o produto escalar

A → ∙ B → = | A → | | B → | c o s ⁡ ( θ )

Substituindo os valores temos:

3,0 i + 5,0 j 10,0 i + 6,0 j = 2 34 . 34 . c o s ⁡ ( θ )

60 68 = cos ⁡ θ

cos ⁡ θ = 0,88

Assim:

θ ≅ 28,3 °

Passo 6

Alternativa c)

Calculando o módulo dos vetores:

A → = - 4,0 2 + 2,0 2

B → = 7,0 2 + 14,0 2

Assim temos:

A → = 2 5

B → = 7 5

Passo 7

Realizando o produto escalar

A → ∙ B → = | A → | | B → | c o s ⁡ ( θ )

Substituindo os valores temos:

- 4,0 i + 2,0 j 7,0 i + 14,0 j = 2 5 . 7 5 . c o s ⁡ ( θ )

0 70 = cos ⁡ θ

cos ⁡ θ = 0

Assim:

θ = 90 °

Resposta

a) θ ≅ 163,7 °

b) θ ≅ 28,3 °

c) θ = 90 °

Exercício Resolvido #2

Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 34 – ex1.93

Um cubo é colocado de um modo que um dos vértices esteja na origem e três arestas coincidam com os eixos x ,   y   e   z de um sistema de coordenadas (Figura 1.43 ). Use vetores para calcular:

  1. O ângulo entre a aresta ao longo do eixo z (linha a b ) e a diagonal da origem até o vértice oposto (linha a d );
  2. O ângulo entre a linha a c (a diagonal de uma das faces) e a linha a d .

Passo 1

Como queremos saber o ângulo entre os vetores, vamos usar o produto escalar, pode ser?

A → ∙ B → = | A → | | B → | c o s ⁡ ( θ )

Passo 2

Vamos escrever o vetor que representa cada segmento que foi dado no problema:

a b → = ( 0,0 , l )

a d → = ( l , l , l )

a c → = ( 0 , l , l )

Passo 3

Alternativa a)

Fazendo o produto escalar entre as linhas a d e a b

a d → ∙ a b → = | a d → | | a b → | c o s ⁡ ( θ )

l , l , l ∙ 0,0 , l = 3 l .   l . cos ⁡ ( θ 1 )

l 2 = l 2 3 cos ⁡ θ 1

Isolando o cos ⁡ θ 1   temos:

C o s θ 1 = 3 3

Logo:

θ 1 = 54,7 °

Passo 4

Alternativa b)

Fazendo o produto escalar entre as linhas a d e a c

a d → ∙ a c → = | a d → | | a c → | c o s ⁡ ( θ )

l , l , l ∙ 0 , l , l = l   3 . l 2 . cos ⁡ ( θ 2 )

2 l 2 = 6 . l 2 cos ⁡ θ 2

Isolando o cos ⁡ θ 2   temos:

C o s θ 2 = 6 3

Logo:

θ 2 = 35,3 °

Resposta

  1. θ 1 = 54,7 °
  2. θ 2 = 35,3 °

Exercício Resolvido #3

Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 28 –Q1.25 e pp 31 – ex1.52

  1. Se A → * B → = 0 , é necessariamente verdadeiro que A = 0   ou B = 0 ? Explique
  2. Use componentes de vetores para provar que dois vetores são comutativos tanto para soma quanto para produto escalar.

Passo 1

Pra fazer essa questão vamos lembrar da fórmula do produto escalar:

A → * B → = | A → | | B → | c o s ⁡ ( θ )

Passo 2

Alternativa a)

Pra fazer essa questão vamos analisar primeiro o lado direito da equação.

Vamos considerar que nem A → , e nem B → tem valor 0 . Assim,

A → > 0

B → > 0

Assim, para o produto escalar ser 0 , o ângulo entre os vetores teria que ser ou 90 ° ou 270 ° , pois assim o cos ⁡ θ = 0

Resumindo: N ã o   p r e c i s a m   s e r   n e c e s s a r i a m e n t e   0

Passo 3

Alternativa b)

Vamos usar dois vetores e suas componentes:

A → = A → x i + A → y j

B → = B → x i + B → y j

Passo 4

Primeiramente vamos provar que dois vetores são comutativos para soma:

A → + B → = A x + B x i + A y + B y j

B → + A → = B x + A x i + B y + A y j

Como achamos o mesmo resultado, provamos que a soma é comutativa

A → + B → = B → + A →

Passo 5

Agora vamos testar o produto escalar:

A → * B → = A x B x + A y B y

B → * A → = B x A x + ( B y A y )

Novamente, como encotramos o mesmo resultado nas duas operações, provamos que o produto escalar também é comutativo

A → * B → = B → * A →

Resposta

  1. Não

Exercício Resolvido #4

Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 33 –ex1.85

Os vetores A e B são desenhados a partir de um mesmo ponto. O vetor A → possui módulo A e forma um ângulo θ A medido supondo-se um rotação no sentido do eixo + O x para o eixo + O y . As grandezas correspondentes do vetor B → são o módulo B e o ângulo θ B . Logo, A → = A c o s θ A i + A s e n θ A j , B → = B c o s θ B i + B s e n θ B j e φ = θ B - θ A é o ângulo entre A → e B → .

  1. Deduza a equação 1.18 partindo da equação 1.21
  2. Deduza a equação 1.22 partindo da equação 1.27

A → ∙ B → = A B cos ⁡ ϕ = A →   B → cos ⁡ ϕ             1.18

A → ∙ B → = A x B x + A y B y + A z B z         ( 1.21 )

C = A B   s e n   ϕ                 ( 1.22 )

C x = A y B z - A z B y       C y = A z B x - A x B z       C z = A x B y - A y B x           ( 1.27 )

Passo 1

Alternativa a)

Partindo da equação 1 ; 21 temos:

A → * B → = A x B x + A y B y + A z B z

Mas como foi dado no enunciado, as componentes z tanto de A →   e de B → são 0 .

A → * B → = A x B x + A y B y

Partindo da equação acima, queremos chegar na equação abaixo:

A → * B → = A B c o s ( φ )

Passo 2

Bom, se olhar pro enunciado e pra equação que estamos partindo, o que podemos mudar ali são as componentes, certo? Não vamos mexer no lado esquerdo, mas a gente pode escrever as componentes de outra forma.

A → * B → = A x B x + A y B y

Lembrando que:

A → = A c o s θ A i + A s e n θ A j

B → = B c o s θ B i + B s e n θ B j

Substituindo na equação temos:

A → * B → = A c o s θ A B c o s θ B + A s e n θ A B s e n θ B

Não vou mudar nada, ok? Só reorganizar :)

A → * B → = A B c o s θ A c o s θ B + s e n θ A s e n θ B

Passo 3

Agora vamos ter que puxar um conceito lá de trigonometria, mas se você não lembrar não esquenta, eu a gente te ajuda ;)

C o s a ± b = cos ⁡ a cos ⁡ b ∓ s e n a s e n ( b )

Mas não é que apareceu a mesma coisa? Agora a gente pode simplificar aquela expressão grandona da nossa expressão

A → * B → = A B c o s ⁡ ( θ A - θ B

Ai a gente troca aquela agora subtração ali e pimba !

A → * B → = A B c o s ( φ )

Passo 4

Alternativa b)

Bom, partindo do que foi dado no enunciado nós temos:

C = A x B y - A y B x

Vamos trocar as componentes da mesma forma. Sem problemas, né?

C = A c o s θ A   B s e n θ B - A s e n θ A B c o s θ B

Vou reorganizar do mesmo jeito que fiz antes. A idéia da alternativa a) é quase a mesma que a idéia da alternativa b)

C = A B c o s θ A   s e n θ B - s e n θ A c o s θ B

Passo 5

Se lembra da trigonometria que a gente usou na alternativa a)? Vamos usar trigonometria agora também!

s e n a ± b = cos ⁡ a sen ⁡ b ± s e n a c o s ( b )

Substituindo na equação que a gente parou ...

C = A B s e n θ A - θ B

Assim:

C = A B s e n φ

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Verdadeiro ou falso: (a) O produto escalar não pode ter unidades. (b) Se o produto escalar de dois vetores diferentes de zero for zero, eles serão paralelos. (c) Se o produto escalar de dois vetores d
Para quaisquer dois vetores A → e B → , mostre que A → ∙ B → = A x B x + A y B y + A z B z . Sugestões: Escreva A → e B → na forma de vetor unitário e use as Equações 6.4 e 6.5.
Dois vetores a → e b → têm componentes, em metros, a x   =   3,2 , a y   =   1,6 , b x   =   0,50 e b y   =   4,5 (a) Determine o ângulo entre a →   e   b → . Existem dois vetores no plano x y que são
O módulo do vetor A é 6,00 unidades, o módulo do vetor B é 7,00 unidades e A · B=14,0 . Qual é o ângulo entre AeB ?
Use a definição de produto escalar , a → . b → = a . b . cos ⁡ ∅ e o fato de que a → . b → = a x b x +a y b y + a z b z para calcular o ângulo entre os vetores a → =3,0 i →+3,0 j →+3,0 k → e b →=2,0 i