Componentes de um Vetor e Vetor Unitário
Teoria
Fala aí! Tá preparado pra entender o assunto de vetores com tudo o que tem direito de uma vez por todas? Então vem comigo dominar os componentes de um vetor, decomposição de vetores, vetor unitário e um pouco mais!
Ah, se quiser dar uma revisada no comecinho de vetores, não deixa de conferir o primeiro link aqui embaixo, lá a gente discute sobre direção, sentido e vetor deslocamento!
⭐ Veja também ⭐
Vetor em Duas Dimensões
Se você se deparasse com um vetorzinho igual esse aqui embaixo, você saberia me dizer as propriedades dele?
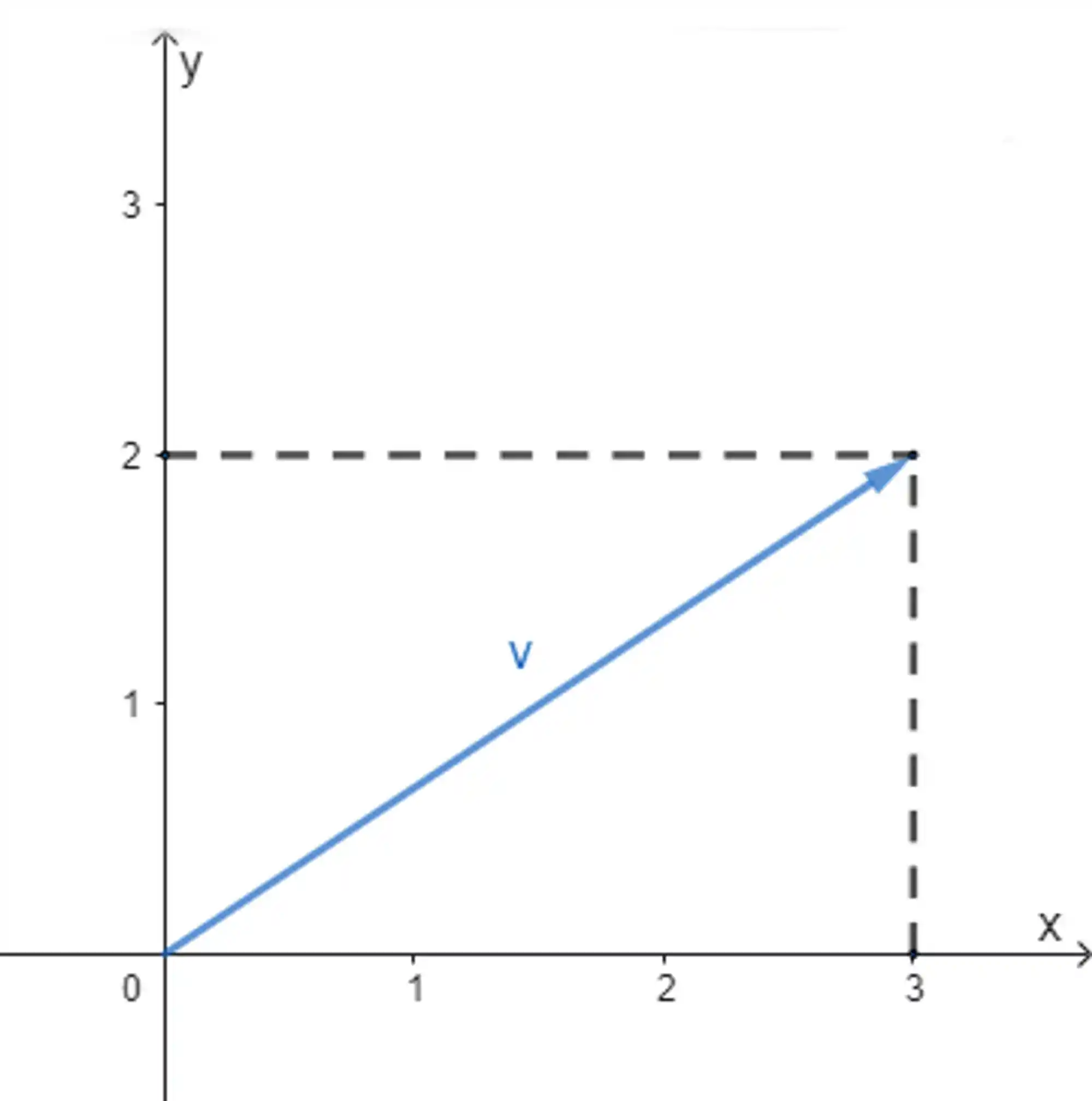
Lembre que um vetor tem módulo, direção e sentido. Mas vamos tratar de uma coisa de cada vez.
Começando pelo tamanho do vetor. O jeito mais fácil de expressar esse cara é por meio das suas componentes.
Quais são as componentes do vetor?
Um vetor de duas dimensões tem duas componentes: uma horizontal e uma vertical. A primeira é a projeção do vetor sobre o eixo x, e a outra é a projeção desse vetor sobre o eixo y.
Força um pouquinho a imaginação aí e tenta pensar em uma lanterna iluminando esse vetor pelo lado de cima. A sombra projetada no eixo x equivale à componente horizontal do vetor (aquela seta em vermelho ali).
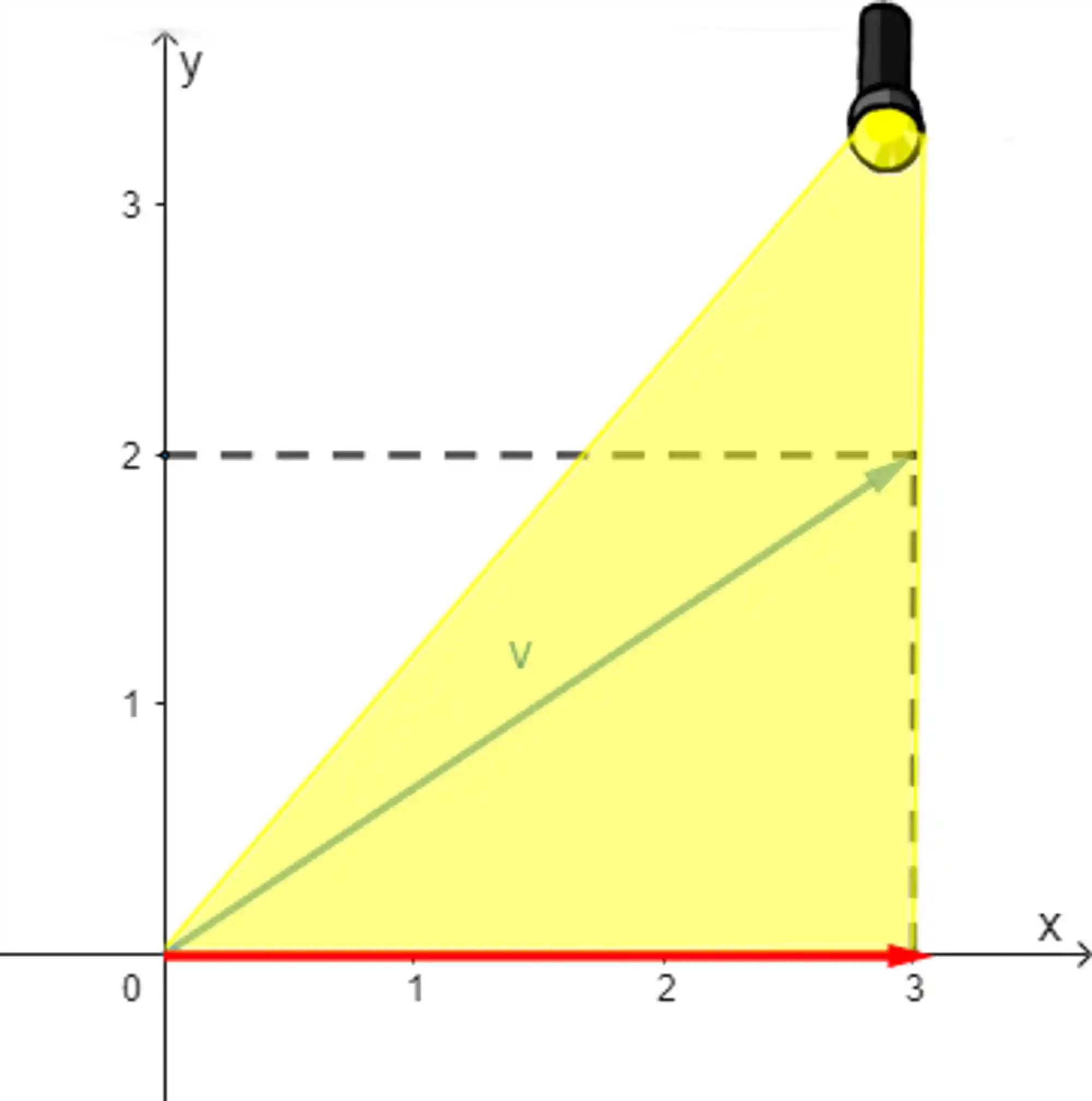
Similarmente, se iluminarmos o vetor pela lateral, vamos obter a projeção da componente vertical lá no eixo y.
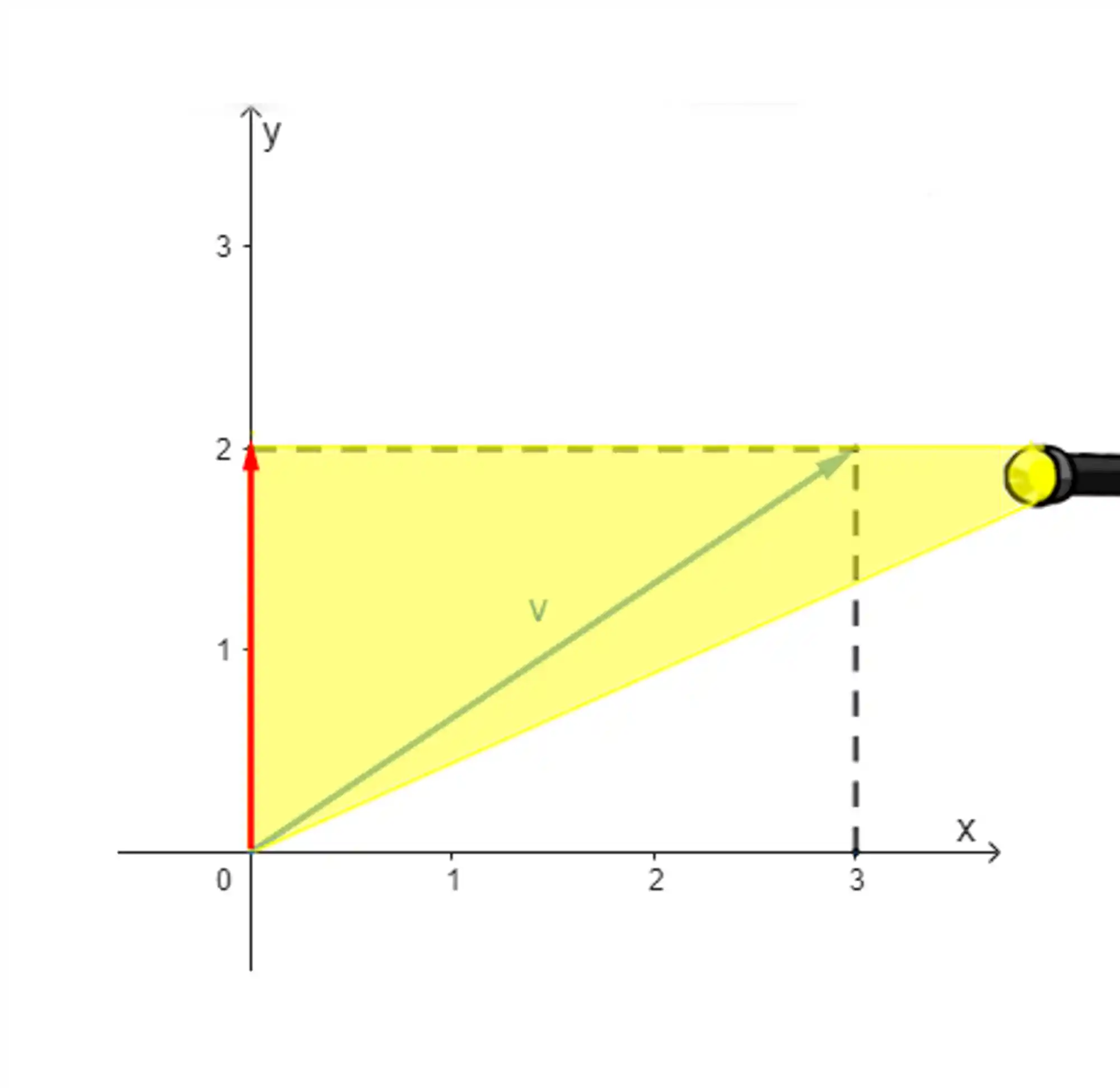
Assim, eu imagino que fique bem mais fácil de perceber o tamanho de cada componente desse vetor.
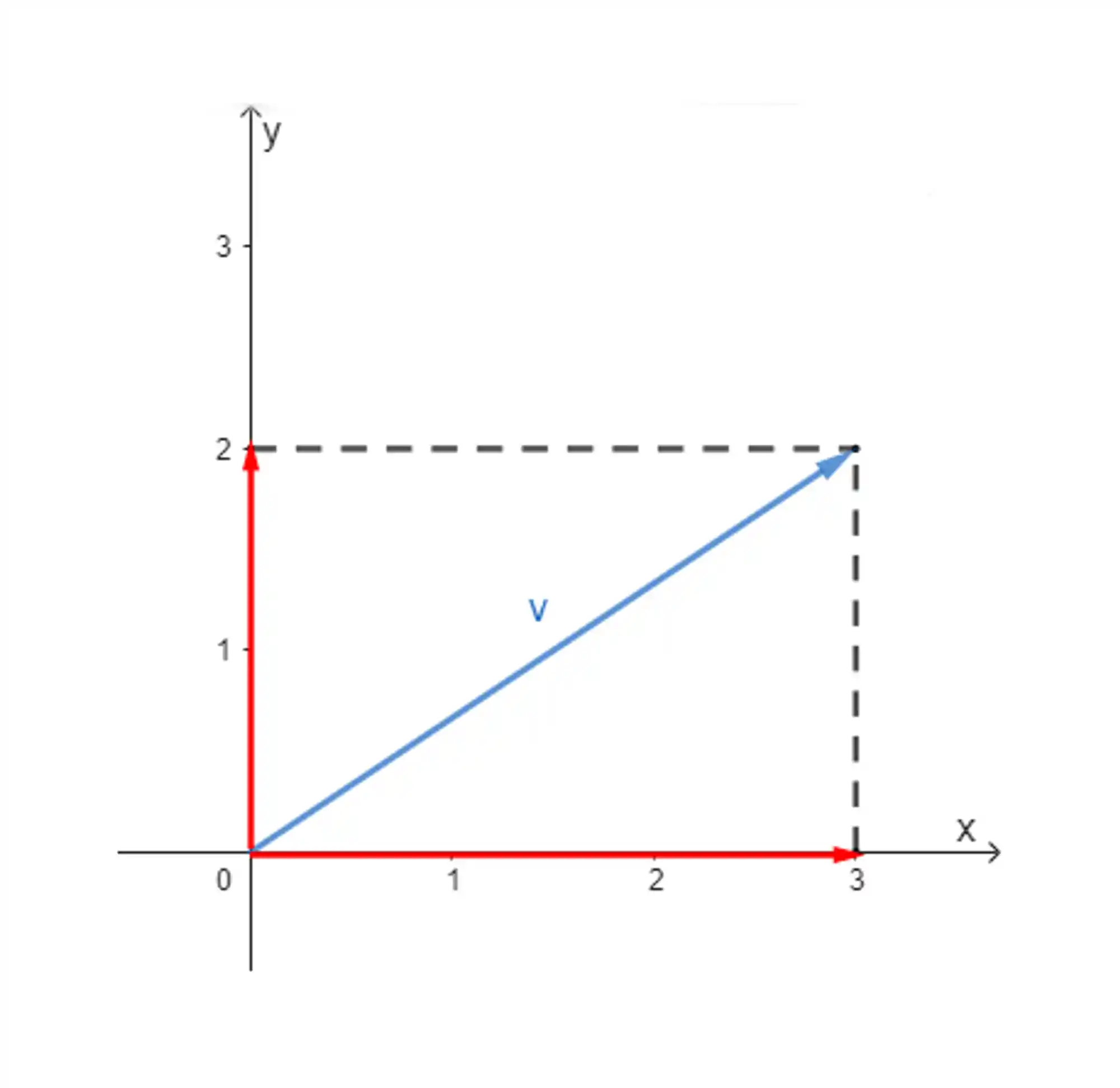
A gente chama a componente horizontal do vetor
Aqui no nosso exemplo, essas componentes valem:
O que significa que nosso vetor
Vetores unitários
Os vetores unitários, ou versores, são vetores paralelos aos eixos cartesianos e de módulo igual a 1. Eles são muito úteis para encontrarmos um jeito de escrever qualquer vetor em função de vetores unitários.
Se liga, o vetor unitário
(E a gente usa o chapeuzinho em vez da setinha em cima da letra quanto tiver falando de um versor).
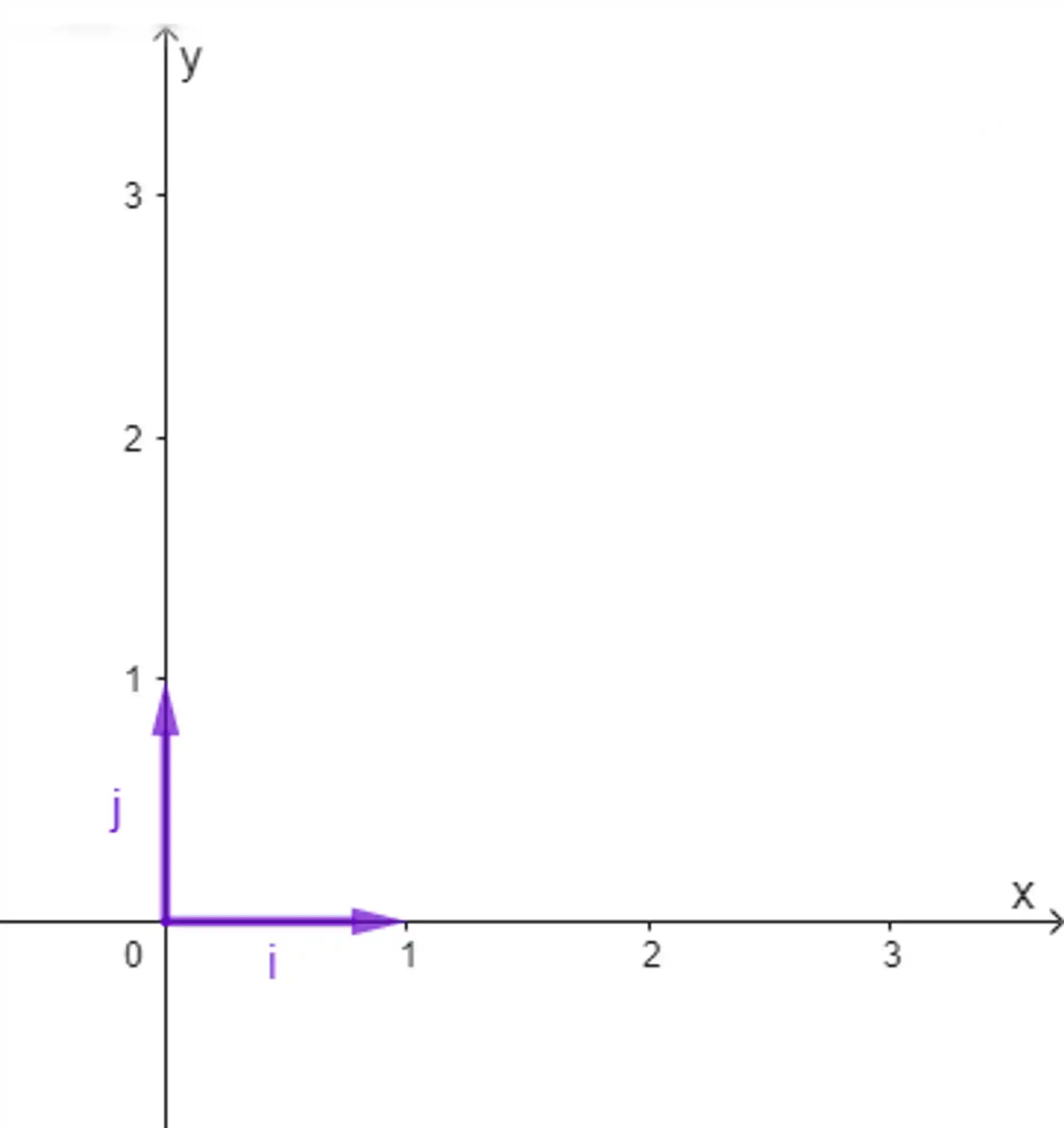
Então, se a gente viu naquele exemplo anterior que o vetor
Módulo de um Vetor
Beleza, a gente sabe encontrar o tamanho das componentes de um vetor, mas muitas vezes o que importa mesmo é o tamanho - o módulo - do vetor original.
Como a gente faz isso?
Olha bem para essa figura aqui e tenta pensar na resposta:
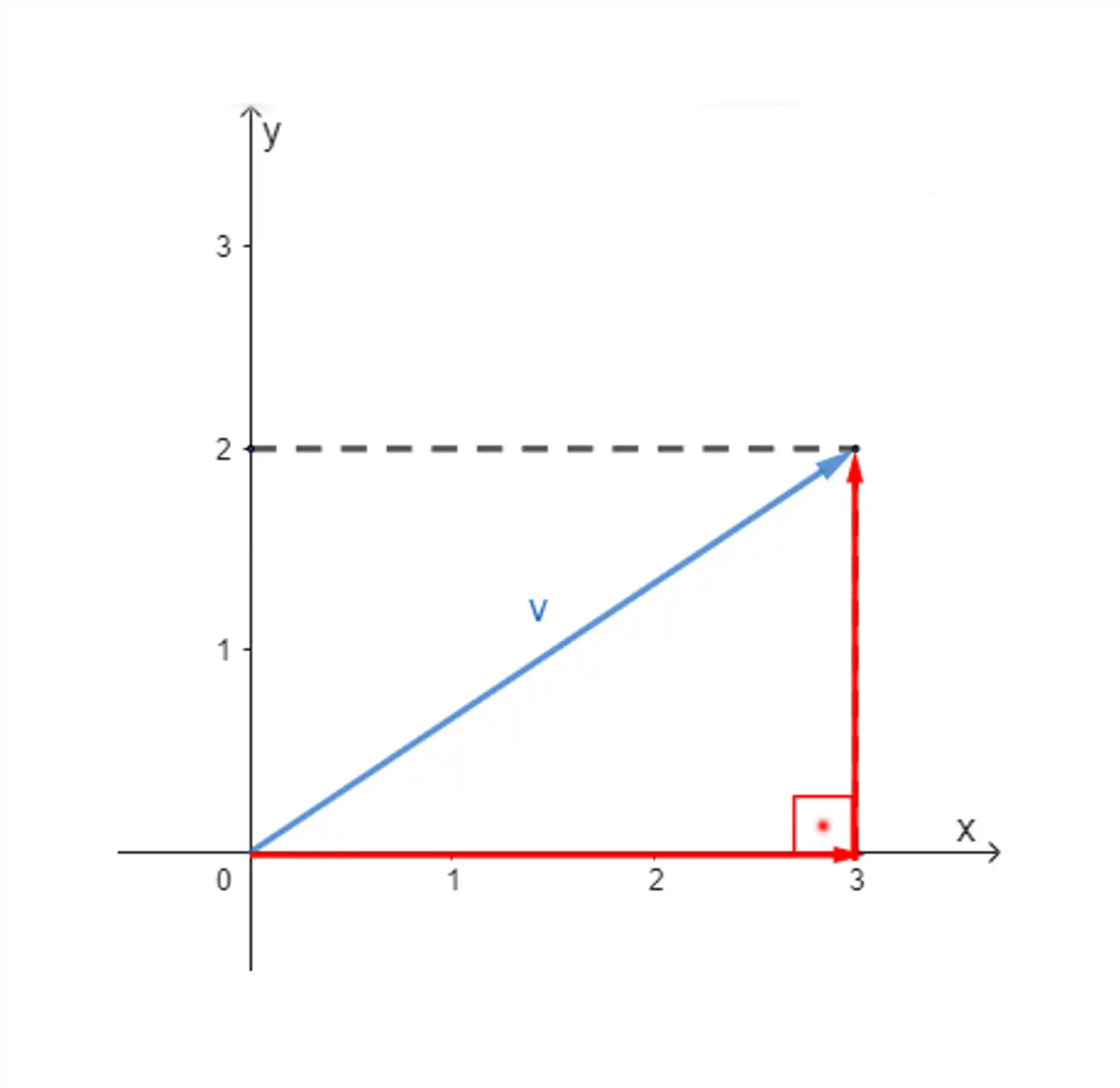
Seria aquilo um triângulo retângulo???? 👀
O módulo do nosso vetor
Decomposição de Vetores
Agora vem a parte mais importante de vetores: a decomposição.
Olha só por que isso é importante, no exemplo que estamos resolvendo desde o começo, eu te dei os valores das coordenadas dos eixos e isso nos permitiu calcular o módulo das componentes e do vetor. Mas e se a gente só conhecesse o valor do módulo do vetor e precisasse encontrar suas componentes?
Já adianto que isso é um problema muuuuuito comum em física, mecânica e várias outras matérias.
Pra resolver isso aí, a gente precisa conhecer a direção do vetor, isto é, o ângulo que ele faz com algum dos eixos.
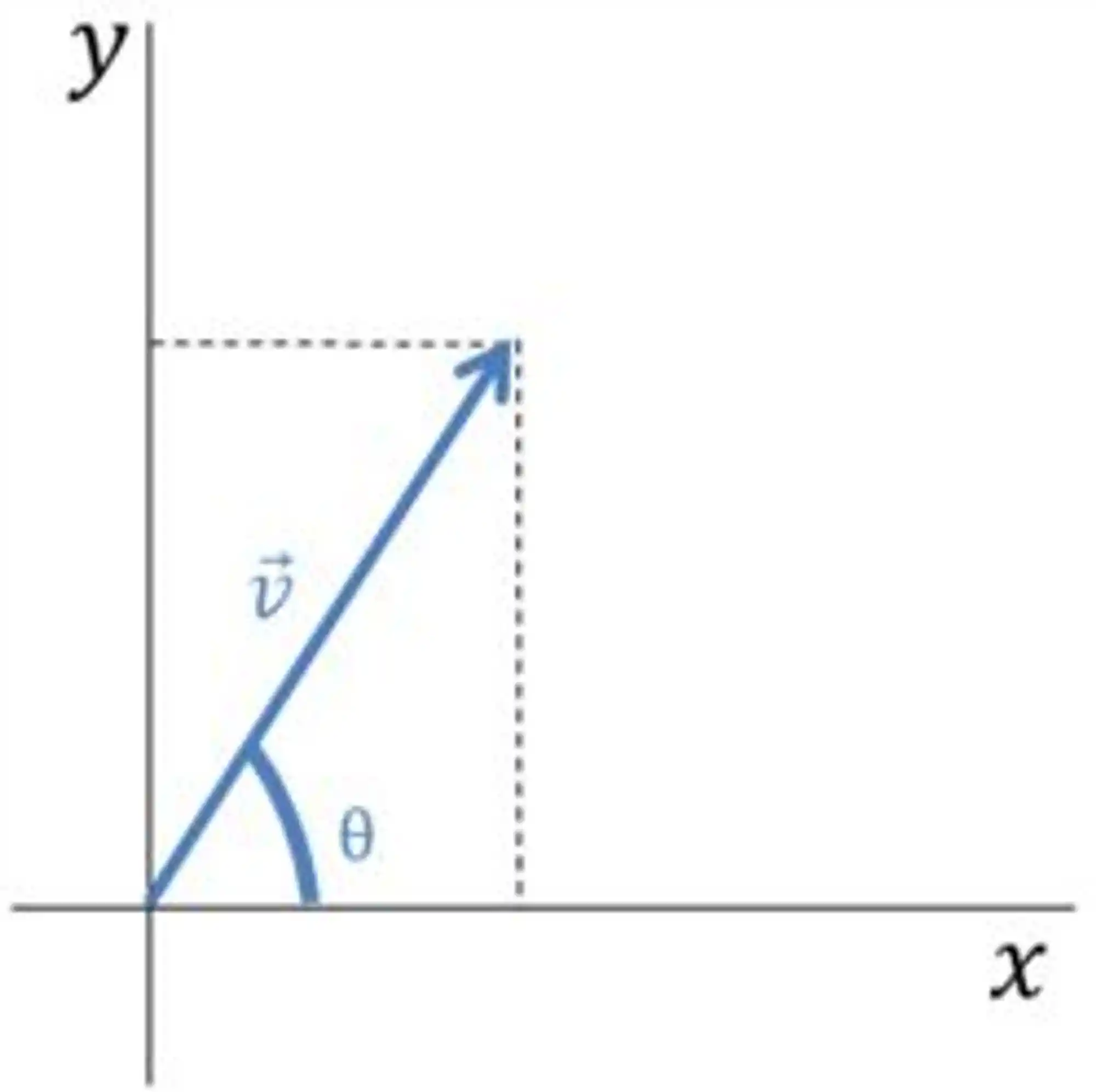
E aí, a gente continua pensando nas relações do triângulo retângulo!
Você precisa lembrar que o seno de um ângulo é igual ao cateto oposto dividido pela hipotenusa.
Então, repare que o cateto oposto nessa imagem aí em cima é a componente vertical de
Com isso:
Só fica ligado, porque, caso o exercício dê o ângulo ali entre
Operações com Vetores
A gente pode fazer somas, subtrações, multiplicações e divisões com vetores! Para todas elas, é importantíssimo você estar dominando essa parte das componentes.
Multiplicação de um Vetor por um Escalar
Uma multiplicação de um vetor por um escalar é quando você multiplica um número por um vetor. Não tem muito segredo não, é só multiplicar o escalar (número) por cada uma das componentes do vetor.
Por exemplo, ainda tratando do vetor que vimos lá no começo. Se quisermos multiplicá-lo por 5:
Soma e Subtração de Vetores
Para fazermos operações de soma ou subtração de vetores, basta somar ou subtrair suas componentes!
Se liga, com os vetores:
Para calcularmos a soma desses vetores, vamos somar a componente i do vetor V com a componente i do vetor U e a componente j do vetor V com a componente j do vetor U. Sem esquecer dos sinais!
E o mesmo vale para a subtração! Só que aí tem que tomar cuidado com o jogo de sinais.
Vetor em Três Dimensões
Tudo o que vimos para vetores de duas dimensões continua valendo aqui. A diferença, é claro, é que agora devemos considerar mais uma dimensão.
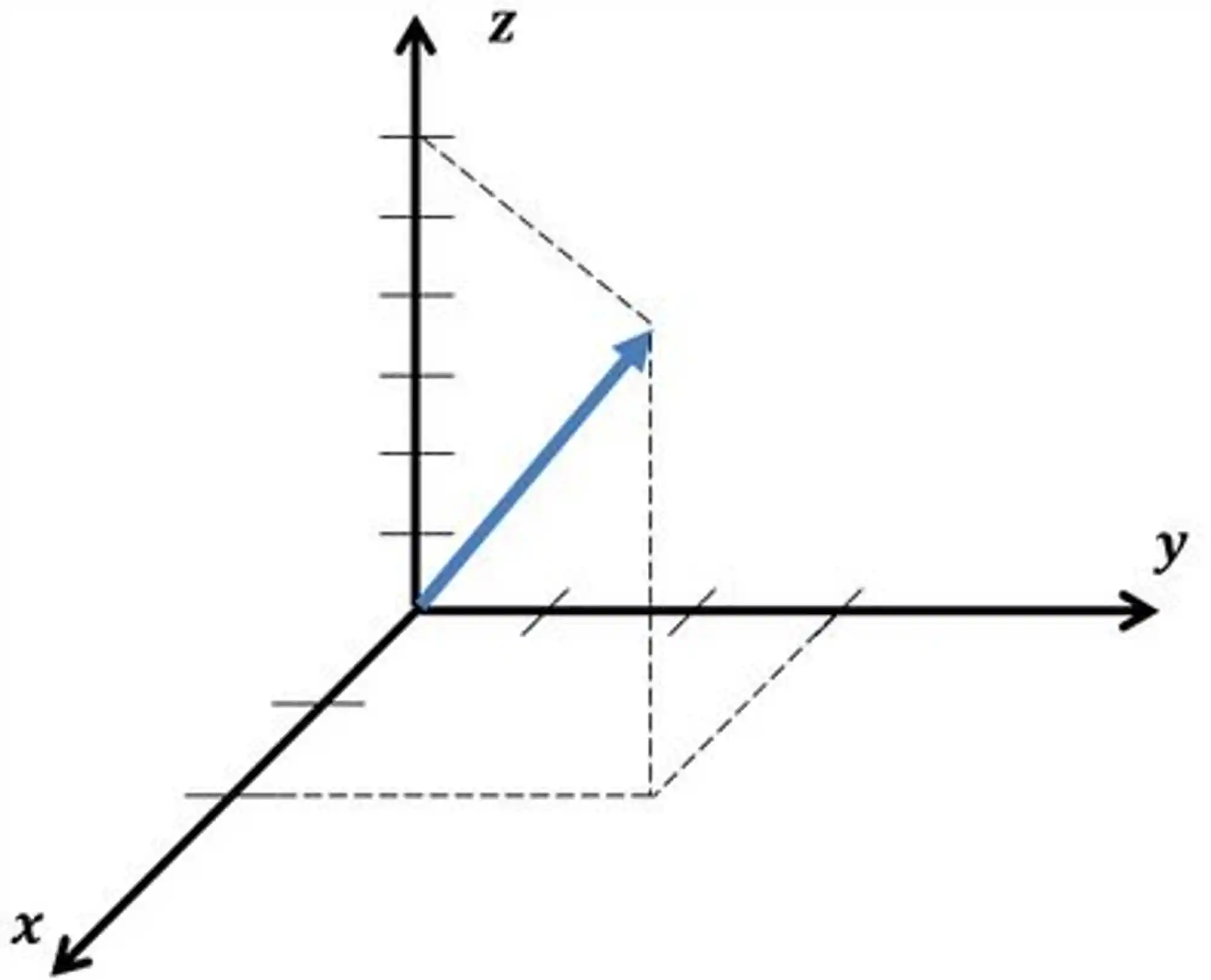
Agora, esse cara tem três componentes:
Pra calcular o módulo de um cara desse tipo, a gente continua tomando a raiz da soma das componentes ao quadrado, igual vimos anteriormente:
Ufaaa, finalizamos!!
Bora praticar com alguns dos nossos exercícios resolvidos passo a passo pra ficarmos bem craques no assunto!
Módulo de um Vetor
Decomposição de Vetores
Operações com Vetores
Vetor em Três Dimensões
Exercícios Resolvidos
Exercício Resolvido #1
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp. 28 – 1.16.
Você pode achar uma grandeza vetorial que possua módulo igual a zero, tendo, porém, componentes diferentes de zero? Explique. É possível o módulo de um vetor ser menor que o módulo de qualquer de seus componentes? Explique
Passo 1
Como a questão trabalha com vetor, módulo e suas componentes, vamos usar a seguinte equação para resolver as questões
Passo 2
Como o módulo do vetor é igual a , temos:
Como as componentes e são diferentes de zero, temos que a soma de dois números positivos tem como resultado , o que seria impossível.
Passo 3
Na equação o módulo do vetor é sempre o módulo de uma componente somado ao módulo da outra componente. Como os dois resultados são sempre positivos, não há como o módulo do vetor ser menor que uma das componentes.
Resposta
Exercício Resolvido #2
TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 22– 10.
Um vetor tem uma componente negativa e uma componente positiva. Seu ângulo, medido no sentido anti-horário a partir do eixo positivo, vale:
- Entre zero e graus
- Entre e graus
- Mais de graus
Passo 1
Vamos desenhar um vetor de acordo com as condições dadas no problema para entendermos o que está acontecendo.
Passo 2
Como podemos ver na figura, o ângulo está entre e . O veto está no segundo quadrante, ou seja, o ângulo é , onde o valor de é .
Passo 3
Quer uma outra idéia pra pensar? Sabemos que as componentes de um vetor são
Como é sempre positivo, o que define a componente ser positiva ou negativa é o e do ângulo. Assim, fica mais tranquilo identificar em qual quadrante está o ângulo. Se a componente é negativa, o é negativo, se a componente é positiva, o é positivo.
Resposta
Exercício Resolvido #3
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 30 – 1.34 - Modificado.
Escreva cada vetor indicado na figura abaixo em termos de vetores unitários .
Passo 1
Para calcular cada componente vamos precisar saber o módulo de cada vetor e a o ângulo que o vetor faz com o eixo
Passo 2
Considerando o ângulo com o eixo temos:
Passo 3
Como o ângulo com o eixo vale , o ângulo com o eixo vale
Assim temos:
Passo 4
Como o ângulo com o eixo val e o ângulo está abaixo do eixo, temos que o ângulo com eixo vale
Assim temos:
Passo 5
O ângulo com o eixo vale
Assim temos:
Resposta
Exercício Resolvido #4
TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 24– 53.
Determine as componentes e dos seguintes três vetores do plano .
- Um vetor deslocamento de que forma um ângulo de no sentido horário a partir do eixo
- Um vetor velocidade de que forma um ângulo de no sentido anti-horário com o eixo .
- Uma força de que forma um ângulo de no sentido anti-horário com o eixo .
Passo 1
Para calcular cada componente vamos precisar saber o módulo de cada vetor e a o ângulo que o vetor faz com o eixo
Passo 2
Considerando o ângulo que o vetor faz com o eixo temos:
Substituindo os valores:
Componentes:
Passo 3
Considerando o ângulo que o vetor faz com o eixo temos:
Substituindo os valores:
Componentes:
Passo 4
Considerando o ângulo que o vetor faz com o eixo temos:
Substituindo os valores:
Componentes:
Resposta
Exercício Resolvido #5
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 30 – 1.40.
Determine o módulo, a direção e o sentido dos vetores representados pelos seguintes pares de componentes:
Passo 1
Cada par de vetores vai formar uma resultante e o módulo dessa resultante é retirado a partir das componentes, é o que faremos para todos os itens, sem mistério.
Para calcular o módulo a partir das componentes vamos utilizar a seguinte fórmula:
Para saber o sentido e a direção do vetor, temos que prestar muita atenção aos sinais das camponentes e saber que:
Passo 2
a)
Substituindo os valores:
Vamos fazer um desenho desse vetor, colocando um sistema de eixos e suas componentes no plano cartesiano.
Agora vamos calcular o ângulo e avaliar se está coerente.
Como a componente x é negativa e a componente y é positiva, o vetor está no segundo quadrante, como no desenho.
O ângulo do que o vetor faz deve ser calculado a partir do primeiro quadrante portanto vamos guardar o valor de em módulo e retirar de como podemos ver na figura.
Pro calculo do ângulo da posição usaremos o módulo de
Mas não se esqueça de tirar esse ângulo dos 180 para ter a posição do vetor:
Passo 3
b)
Substituindo os valores:
Vamos de novo fazer um desenho, aqui poderemos representar somente os sinais pra avaliar a coerência do ângulo encontrado.
Vamos calcular o valor de , começando pela sua tangente.
Também usaremos o módulo ainda que pro caso positivo não faça diferença alguma:
Como a componente negativa e a componente é negativa, o vetor esta no terceiro quadrante. Nesse caso o ângulo que o vetor faz com o primeiro quadrante é:
Passo 4
c)
Substituindo os valores:
Vamos avaliar na figura a posição do vetor e o seu ângulo:
Calculando o valor de
Como a componente x é positiva e a componente y é negativa, o vetor esta no quarto quadrante.
Nesse caso calculamos o ângulo
E subtraímos de o seu módulo:
Logo:
Resposta
Exercício Resolvido #6
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp. 25 - Modificado
O vetor tem componentes , ; o vetor tem componentes ,
- Encontre
- Calcule o módulo do vetor anterior
Passo 1
a)
Temos as componentes do vetor , ele fica
Passo 2
Temos as componentes do vetor , ele fica
Passo 3
Agora que temos os vetores e podemos encontrar somando as componentes de e
Passo 4
b)
Para encontrar o módulo de fazemos
Resposta
Exercício Resolvido #7
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 30 – 1.45.
Use componentes de vetores para determinar o módulo e a direção do vetor necessários para equilibrar os dois vetores demonstrados na Figura . Considere o vetor ao longo do eixo e considere o eixo ortogonal a ele, no sentido da direita.
Passo 1
O primeiro passo da questão é achar o vetor resultante da soma dos vetores dados. Depois que acharmos o vetor resultando, para estar equilíbrio, as componentes precisam ser nulas, ou seja, basta adicionarmos um vetor contrário ao vetor resultante.
Passo 2
Para somar dois vetores vamos decompor cada um deles, para isso, podemos observa-los de uma outra forma:
Decompondo o vetor :
Decompondo o vetor
Passo 3
Assim, o vetor resultante da soma dos vetores
Passo 4
Como o vetor necessário equilibrar precisa ser oposto ao vetor resultante temos:
Passo 5
Para calcular o módulo do vetor vamos usar suas componentes:
Passo 6
Para saber o sentido e a direção do vetor, vamos usar suas componentes para saber o ângulo em relação ao eixo
Calculando na sua calculadorazinha, você vai achar:
Mas CALMA AÍ, antes tem que dar uma olhada nas componentes!
Como a componente em é positiva e a componente é negativa, o vetor está no segundo quadrante. Logo:
Resposta
Exercício Resolvido #8
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp. 32 – 1.71- Modificado.
Você deseja programar o movimento do braço de um robô em uma linha de montagem para se mover no plano . Seu primeiro deslocamento é ; seu segundo deslocamento é , cujo módulo é igual a , formando um ângulo de , medido considerando-se uma rotação do eixo para o eixo . A resultante dos dois deslocamentos deve também possuir módulo igual a , porém formando um ângulo de , medido considerando-se uma rotação de eixo para o eixo .
- Desenhe um diagrama para escala aproximada para estes vetores.
- Ache os componentes de
- Ache o módulo e a direção de
Dados:
Passo 1
Bom, sabemos que a partir de módulo de um vetor e do seu ângulo conseguimos todas as informações das componentes dele, certo? Foi dado no problema:
Assim podemos decompor cada vetore e analisar suas componentes. Vamos fazer o movimento do robô?
Passo 2
Alternativa a)
Pra fazer esse diagrama vamos fazer primeiro o vetor e depois o vetor que são os vetores que nós conhecemos. Vamos usar o método geométrico.
Passo 3
Alternativa b)
Decompondo o vetor .
Substituindo os valores temos:
Passo 4
Decompondo o vetor .
Substituindo os valores temos:
Passo 5
Assim, substituindo na equação os valores das componentes do vetor , temos:
Analisando cada componente separadamente temos:
Assim:
Passo 6
Alternativa c)
Para achar o módulo de vamos usar aquela fórmula das componentes, se lembra?
Substituindo os valores temos:
Passo 7
Para achar o ângulo, só pela componentes já da pra saber que ele está no primeiro quadrante.
Tirou isso da onde ???????
As duas componentes são positivas, ou seja, o seno e o cosseno do ângulo do vetor são positivos.
Agora vamos usar as componentes para achar o ângulo:
Fazendo o cálculo desse ângulo pela calculadora, vamos ter que:
Resposta
Exercício Resolvido #9
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 32 – 1.76.
Em um vôo de treinamento, uma aprendiz de piloto voa de Lincoln, no Estado de Nebraska, até Clarinda, no Iowa; a seguir até St. Joseph, no Missouri: depois até Manhattan, no Kansas, como na figurinha abaixo. Os ângulos formados pelos deslocamentos são medidos em relação ao norte: significa sentido sul para o norte, é o leste, é o sul e é o oeste. Use o método dos componentes para achar:
- A distância que ela terá de voar para voltar para Lincoln
- A direção (em relação ao norte) que ela deverá voar para voltar ao ponto de partida. Ilustre a solução fazendo um diagrama vetorial.
Passo 1
Nesse exercício, além de dar aquele rolé pelos Estados Unidos, vamos trabalhar com deslocamentos. Se lembra, laaaaa na teoria, dos carrinhos? Então, como deslocamentos são vetores e no final ele quer voltar para o mesmo ponto, temos que deslocamento total é zero, ou seja, a soma vetorial precisa ser zero.
Passo 2
Alternativa a)
Como o deslocamento total é zero, temos:
Onde:
Passo 3
Agora vamos analisar componente por componente, começando pela componente para o leste (ou eixo ).
Para calcular a componente em x do primeiro vetor, temos o seguinte:
Como o ângulo se refere ao ângulo que ela faz com o eixo , temos que a componente em será o módulo do vetor multiplicado por (e não por um cosseno como estamos acostumados)!
Logo, teremos:
Passo 4
Agora vamos analisar componente por componente, começando pela componente para o norte (ou eixo ):
Passo 5
Para calcular o módulo, vamos usar a fórmula das componentes:
Passo 6
A ângulo do vetor, em relação ao norte, é:
Como o do ângulo é negativo e o do ângulo é positivo, o ângulo está no quarto quadrante.
Repare que agora o quarto quadrante é o quadrante formado pelo eixo negativo e o positivo:
Isso porque estamos iniciando a contagem a partir o eixo , que é o norte, e vai no sentido horário. Normalmente, a gente inicia do eixo positivo e vai em sentido anti-horário... Beleza?? Só para não confundir!
Resposta
a)
b)
