Leis de Kepler
Produzido por Ludovic BeghinTeoria
Fala aí, você chegou no Responde Aí. E vamos estudar tudo sobre Leis de Kepler.
As Leis de Kepler
Você já parou pra pensar em como os planetas orbitam o sol? Você já parou pra pensar em o que é uma órbita? Pois um tal de Kepler, já
Uma órbita é quando um corpo gira ao redor de outro!
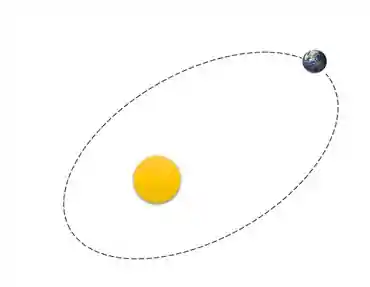
As Leis de Kepler são três leis que falam como funcionam as órbitas planetárias. Essas leis são:
- 1ª Lei de Kepler: Lei das órbitas elípticas.
- 2ª Lei de Kepler: Lei das áreas.
- 3ª Lei de Kepler: Lei dos períodos.
1ª Lei de Kepler
A primeira lei explica como funciona a órbita e a posição do sol, vamos ver exatamente o que o Kepler definiu e tentar decifrar pra nós a utilidade da lei.
“Cada planeta se move em uma órbita elíptica, com o Sol ocupando um dos focos da elipse”.
Então a gente pode desenhar a órbita em forma de elipse, e os focos tem a mesma distância do centro da elipse e ficam posicionados mais ou menos assim.
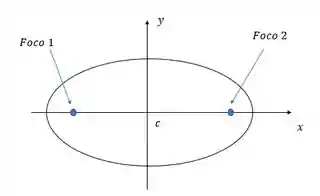
E sobre os pontos da trajetória elíptica que o planeta pode estar, existem dois específicos que são os mais famosos. São eles o Periélio e o Afélio!
- Afélio: ponto da órbita mais longe do sol.
- Periélio: ponto da órbita mais perto do sol.
2ª Lei de Kepler
A segunda lei de Kepler já é um pouco mais prática e ajuda a gente a encontrar relações entre as distâncias percorridas pelo planeta em diferentes pontos da órbita, saca só:
“A linha que liga o Sol a um planeta varre áreas iguais a intervalos de tempos iguais”.
Podemos dizer que razão entre uma área qualquer
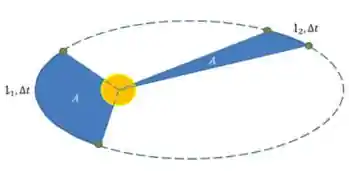
Outra coisa que podemos deduzir é que: Um planeta fica mais rápido quando está próximo do sol, e mais devagar quando está longe do sol.
Combinando isso com a fórmula ali em cima, podemos dizer que a velocidade do afélio multiplicada pelo raio do afélio, tem que ser igual a velocidade do periélio multiplicada pelo raio do periélio.
3ª Lei de Kepler
Essa lei nos dá uma relação com o período, vamos dar uma olhada no enunciado e entender.
“Os quadrados dos períodos de translação dos planetas são proporcionais aos cubos dos semi-eixos maiores de suas órbitas.”
Onde
Videoaula
Que aprender mais? Então se liga nessa aula
Agora que você sabe tudo das Leis de Kepler, que tal tentar uns exercícios aqui em baixo 👇