Túnel Através de um Planeta

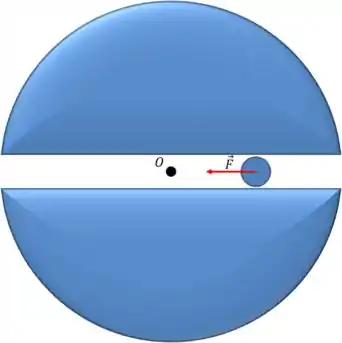
Bom, aprendemos que, em uma esfera maciça, quando queremos calcular a força gravitacional quando , temos que acumular a massa da esfera que dista do centro e calcular a força gerada por ela, certo? Tem um tópico explicando isso tim tim por tim tim antes desse aqui, heim!? ;)

Se fizermos isso agora, conseguimos entender o porquê da força ser horizontal, já que ela está simplesmente apontando pro centro do planeta.

Então, a força , como mostrada no desenho, considerando que o objeto tem massa , é dada por:

No entanto, podemos melhorar isso aí, pois de acordo com o nosso desenho acima:

Substituindo:

O que faz sentido, já que, quando for negativo, a força inverterá seu sentido.

OPAAA! Se me lembro bem, esse é um tipo conhecido de força, certo? Como é uma constante, temos a equação de uma força em MHS (Movimento Harmônico Simples) da forma:

Onde:

Bem cara de força elástica, não é mesmo? :o

“Que maneiro! Então quer dizer que, se não houver atrito, uma partícula em um túnel ia ficar oscilando ali indeterminadamente?”

Isso mesmo! A gente pode calcular até a frequência dessa oscilação! Saca só:

Lembra como é a frequência angular no MHS? É assim ó

Assim com a nossa “constante de mola”

Bizarro né?! Lembrando que com essa frequência angular podemos calcular a frequência e o período desse movimento

Obs: Não confunda essa frequência que acabamos de calcular com a frequência de um corpo orbitando um planeta! É que as duas frequências são iguais (em valor) mas têm significados totalmente diferentes. Uma frequência é a de um MHS e a outra é de uma rotação!

Não tem muito o que inventar mais sobre esse assunto, mas não deixe de praticar. Bora lá!