Força Peso e Força Normal
Teoria
Fala aí! Bem vindo ao RespondeAí! Nessa página vamos continuar nosso estudo de Leis de Newton, e falar sobre a Força Peso e a Força Normal.
Essas forças muitas vezes apresentam uma relação entre si, e por isso são ensinadas juntas. Vamos falar primeiro sobre a força Peso.
Força Peso
Na segunda Lei de Newton aprendemos que uma força é criada quando aplicamos uma aceleração em alguma massa:
Nós também sabemos que a gravidade é um tipo de aceleração, e que todo objeto na superfície da terra está exposto a aceleração da gravidade da terra, logo, todos a todo momento sofrem a influenciam da aceleração gravitacional.
Ou seja, a aceleração gravitacional, gera em todos os corpos uma força Peso, que aponta na direção do chão, e que tem fórmula:
Por isso que os objetos caem, porque a força Peso acelera eles para baixo:
Tudo bem, e a força Normal?
Força Normal
A força Normal é aquela que está relacionada com o contato de um objeto em alguma superfície, você lembra da terceira lei de newton? A lei da ação e reação? Sempre que um objeto encosta em uma superfície a superfície gera uma força de reação ao toque e chamamos essa reação de normal.
Essa força é sempre perpendicular a superfície e por isso quando estamos lidando com situações na vertical, acaba-se criando uma relação entre a força Peso e força Normal. Vamos pensar na seguinte situação, uma mação apoiada sobre uma mesa:
Nessa situação temos um sistema em equilíbrio, logo a aceleração resultante do sistema tem que ser
Podemos representá-las assim:
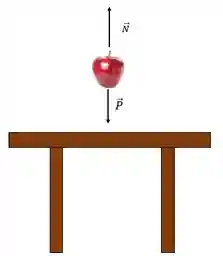
Como o objeto está em equilíbrio:
E as forças que atuam no corpo são:
Combinando as duas equações:
Essa relação é válida porque temos apenas essas duas atuando na maçã no eixo vertical. Por exemplo se eu fosse com o meu dedo a pressionasse a maça contra a mesa, essa relação já não seria mais verdadeira, o sistema continuaria em equilíbrio, mas teríamos uma força mais na relação. Se chamasse a força que eu exerceria com meu dedo de
Repara que a força entra como negativa na equação porque ela aponta na mesma direção do Peso. E teríamos uma nova relação:
No nosso site você encontra diversos exercícios resolvidos, assim como tópicos completos e resoluções Passo a Passo para você mandar bem em Física na faculdade, aproveita e confere um de nossos exercícios resolvidos para você mandar bem na sua prova!
Exercício
Acompanhe um exercício tirado do livro do Halliday, Fundamentos de Física, Volume I, de um exercício de forças, força Peso e força Normal!
Força Normal
Exercício
Exercícios Resolvidos
Exercício Resolvido #1
UNICAMP-P1-2015.1-Q10
Uma pessoa pula para cima do modo tradicional, flexionando os joelhos e os esticando rapidamente. Durante o pulo, enquanto ainda há contato entre os pés da pessoa e o chão, podemos afirmar que:
- A 3ª lei de Newton momentaneamente perde a validade, uma vez que a força Normal exercida pelo chão é maior que a força Peso.
- A 3ª lei de Newton não se aplica a este caso, uma vez que o movimento da pessoa é acelerado.
- A força Peso e a força Normal exercida pelo chão formam um par de ação e reação.
- Não há uma reação à força Normal exercida pelo chão, por isso a pessoa consegue saltar.
- Nenhuma das anteriores.
Passo 1
Vamos analisar as alternativas uma a uma.
a) A terceira lei de Newton nunca perde a validade. A força Normal exercida pelo chão de fato é maior que a força Peso, mas este não constitui um par ação e reação! A força Normal exercida pelos pés sobre o chão é o verdadeiro par ação-reação da força Normal exercida pelo chão sobre os pés. A força gravitacional exercida pelo corpo da pessoa sobre a Terra é o par ação-reação da força gravitacional exercida pela Terra sobre a pessoa (força Peso).
b) A terceira lei de Newton não depende do referencial estar em repouso ou em movimento. Ela sempre pode ser aplicada.
c) Não, como vimos no item , eles não são um par ação e reação
d) Há sim uma reação a esta força. Como em todo par ação-reação, cada força do par atua em um corpo diferente, como já dissemos no item .
e) Alternativa correta.
Resposta
Letra (e)
Exercício Resolvido #2
UNICAMP-P1-2014.1B-Q12
Um homem de está em um elevador, que tem aceleração de para baixo. A força exercida pelo homem sobre o chão do elevador é aproximadamente:
a)
b)
c)
d)
e)
Passo 1
Vamos analisar as forças atuantes no sistema:
Temos que:
Pela segunda lei de Newton:
Substituindo na equação:
Resposta
Alternativa
Exercício Resolvido #3
UFRJ-Física 1-P1 2014.1 ME7
Em uma balança dentro de um elevador em movimento vertical é colocado um bloco de massa e a balança indica sobre seu prato uma força vertical de módulo exercida pelo bloco. Em relação a sistema de eixos , fixo na Terra, com vertical orientado para cima a aceleração do elevador é dada por uma componente igual a
- ;
- ;
- ;
- ;
- Todas as opções acima estão erradas.
Passo 1
Os dados do problema são
Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.
Vamos responder as perguntas do passo a passo para colocar as forças que atuam na balança
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
Sim, ele tem massa.
Sim, o sistema está apoiado no chão.
Não, não existe fio atuando.
Não, não existe mola atuando.
Apesar de o elevador ter o seu fio, estamos preocupados apenas com o bloco, então as forças que atuam nesse são apenas a normal e peso.
O seu DCL ficará
Passo 2
Imaginando um movimento na vertical
então
Resposta
Letra D
Exercício Resolvido #4
UNICAMP-P1-2015.1-Q11
Uma pessoa de está de pé sobre uma balança de mola presa ao chão de um elevador. Quando o elevador inicia a subida, ele acelera para cima a durante , e ao chegar ao andar desejado ele desacelera à mesma taxa. A escala da balança mostra os seguintes valores na partida, durante a viagem, e na chegada, respectivamente:
- , e
- , e
- , e
- , e
- , e
Passo 1
A balança mede a força normal atuando sobre ela. Na subida, partindo do fato que a força resultante sobre a pessoa é a que causa a sua aceleração e escolhendo um eixo vertical para cima temos:
Substituindo os dados:
Passo 2
Agora, durante a maior parte do percurso, o elevador não sofre aceleração. A aceleração é só para mover o elevador no estado inicial ou para freia-lo. Então, o elevador se move a velocidade constante, ou seja:
Passo 3
E por fim, ao final do trajeto o elevador desacelera, ou seja, a aceleração é negativa:
Substituindo os dados:
Resposta
Letra (e)
Exercício Resolvido #5
PUCRIO-P1-B-2014.1 Q1.3
Uma força igual a (N) atua sobre o bloco , como mostrado na figura abaixo, fazendo com que os blocos , e se desloquem sobre uma superfície horizontal sem atrito. Considere que as massas dos blocos são , e , respectivamente. Encontre o vetor força que o bloco exerce sobre o bloco .
a)
b)
c)
d)
Passo 1
Podemos tratar o sistema como um único bloco e aplicar a segunda lei de Newton para encontrar a aceleração:
Logo, se analisarmos o bloco separadamente e substituirmos essa aceleração:
Podemos agora aplicar a terceira lei de Newton:
Resposta
Letra
Exercício Resolvido #6
USP- P1-2015-Q1
A figura abaixo representa dois blocos e , de massa e , respectivamente, em contato e apoiados sobre uma superfície lisa sem atrito. Uma força é aplicada ao bloco empurrando todo o conjunto. Assinale a alternativa que contém a magnitude (módulo) das forças de contato exercidas pelo bloco 1 sobre o bloco 2 e pelo bloco sobre o bloco .
(a) e .
(b) e .
(c) e .
(d) e .
(e) e
Passo 1
Vamos começar fazendo o diagrama de blocos para raciocinar melhor =)
Passo 2
Muito bem, vamos primeiro calcular a aceleração do conjunto:
Entretanto, as forças e são pares ação e reação. Portanto, elas são iguais em módulo! Logo, elas iram se anular nesse cálculo. Ficando apenas com:
Passo 3
Agora, para encontrar a magnitude desse par ação e reação, basta utilizar a 2ª lei de Newton nos blocos separadamente, pois a aceleração tem que continuar sendo .
Para o bloco :
Logo:
Resposta
Letra
Exercício Resolvido #7
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : LTC, 2008, pp. 120-47
Na Fig. 5-46, um bloco de massa é puxado ao longo de um piso horizontal sem atrito por uma corda que exerce uma força de módulo e ângulo . (a) Qual é o módulo da aceleração do bloco? (b) O módulo da força é aumentado lentamente. Qual é o seu valor imediatamente antes de o bloco perder contato com o piso? (c) Qual é o módulo da aceleração do bloco na situação do item (b)?
Passo 1
Temos aqui uma situação onde forças agem em um bloco, onde temos como dados:
- Massa do bloco;
- Valor das forças que agem nele
E nos é pedido a aceleração desse bloco. O que podemos fazer? Vamos usar a segunda lei de Newton! Que relaciona exatamente o que temos com o que queremos.
Passo 2
Primeiramente vamos fazer o Diagrama de Corpo Livre, atentando para a existência da força normal. No diagrama também já faremos a decomposição da força na direção normal dos eixos e .
Se aplicarmos agora a segunda lei de Newton independentemente para cada eixo. No eixo , temos:
Substituindo os valores de e , chegamos ao seguinte valor para :
Já no eixo , temos:
Aqui esbarramos em um problema. Nós não temos o valor nem de e nem de , portanto, essa equação não teria solução. No entanto, como sempre na física, buscaremos argumentos físicos para encontrar valores de coisas que a gente não sabe. Perceba que a jogada que vamos usar aqui dará spoiler para a solução da letra (b), se liga:
Concorda que, se o corpo tivesse aceleração vertical pra cima, ou seja, se fosse diferente de 0, a primeira coisa que aconteceria seria o corpo perder contato com o chão? E concorda também que se existisse essa perda de contato, a normal se tornaria nula? Então vamos lá: se a componente vertical de , , for maior ou igual ao peso, ela será grande o suficiente para tirar o corpo do chão e acarretar em tudo que foi perguntado.
Já que temos o valor da componente vertical e o valor do peso, podemos descobrir qual é essa relação!
Certo, então o peso é maior que a componente vertical e o corpo permanece no chão, com isso, concluímos que, nessas condições:
Para responder a letra (a), vamos então usar os resultados obtidos:
Passo 3
Com o spoiler que demos na letra (a), a gente consegue descobrir de cara o que temos que fazer para descobrir módulo da força quando o corpo começa a perder o contato com o solo. Precisamos também observar que neste momento, o corpo continua sem aceleração vertical. Para matar o item, basta fazer a força normal e a aceleração em ser zero! Portanto, aplicando a segunda lei novamente no eixo , temos:
E entã, substituindo os valores conhecidos, temos:
Passo 4
Já usamos na letra (b) que a aceleração vertical no instante em que o bloco perde o contato com o chão é nula, portanto, para acharmos o módulo da aceleração, basta acharmos a aceleração no eixo . Aplicando a segunda lei no eixo encontramos:
Substituindo o valor de e usando o valor de que encontramos na letra (b), temos:
Já confirmamos que a aceleração nesse instante é horizontal, portanto:
Resposta
Exercício Resolvido #8
UERJ-LISTA 1-2
Uma corrente com quatro elos ( cada) é puxada para cima por uma força vertical (assinalada na figura abaixo) de módulo igual a .
Desenhe um diagrama das forças que atuam sobre cada elo.
Escolha um sistema de referência e escreva as forças nesse referencial.
Escreva as leis de Newton para o problema e deduza as equações pertinentes.
Calcule a aceleração da corrente.
Calcule as forças que atuam nos elos.
Passo 1
e
Passo 2
Vamos usar a segunda lei de Newton () para o sistema.
Pela segunda lei também sabemos que como todos os elos tem a mesma massa, então, .
Além disso, pela terceira lei de newton sabemos que os pares ação e reação tem o mesmo valor mas com sentidos diferentes. Portanto, . Logo, eles se cancelarão no sistema, sobrando apenas.
Passo 3
Basta resolver a equação acima, substituindo os valores, e acharemos a aceleração
Passo 4
Vamos primeiro ver as forças que já temos.
Agora, para achar as forças que faltam é só aplicar a segunda lei de newton em cada elo, separadamente.
No primeiro elo:
Já no segundo, a gente vai ter:
E, por fim, no terceiro:
Resposta
Exercício Resolvido #9
PUCRIO-P1-2015.1 Q2
Considere .
Um bloco de massa , é colocado sobre uma mesa 1 de massa . Este conjunto (mesa 1 e bloco ) é então colocado sobre a mesa 2 de massa . Por fim todo o novo conjunto (mesa 1, mesa 2 e bloco) é colocado dentro de um elevador em repouso como mostra a figura. Despreze a resistência do ar e o atrito entre os corpos.
a) Desenhe o diagrama de corpo livre para mesa 1, mesa 2 e bloco, para o caso estático.
b) O elevador sobe com aceleração . Determine o módulo da força normal realizada pela mesa 1 sobre a mesa 2. Considere apenas um par de forças normais entre as mesas 1 e 2.
c) O elevador desce com aceleração . Determine o módulo da força normal realizada pela mesa 1 sobre a mesa 2. Considere apenas um par de forças normais entre as mesas 1 e 2.
Passo 1
a)
Basta ficar atento aos pares ação reação. O diagrama fica assim:
Passo 2
b)
Como já sabemos que a aceleração vale , vamos aplicar a segunda lei de Newton aos objetos separadamente.
Aplicando ao bloco :
Aplicando agora a segunda lei de Newton à mesa :
Como são pares ação reação, então:
Passo 3
c)
Vamos fazer a mesma coisa que no item anterior, só que agora a aceleração vale , vamos aplicar a segunda lei de Newton aos objetos separadamente.
Aplicando ao bloco :
Aplicando agora a segunda lei de Newton à mesa :
Como são pares ação reação, então:
Resposta
a)
b) ;
c)