Em ou , Emanuel Zacchini levou seu número de bala humana a novas alturas: disparado por um canhão, passou por cima de três rodas-gigante antes de cair em uma rede (Fig.4-39). (a) Tratando Zacchini como urna partícula, determine a que distância vertical passou da primeira roda-gigante. (b) Se Zacchini atingiu a altura máxima ao passar pela roda-gigante do meio, a que distância vertical passou dessa roda-gigante? (c) A que distância do canhão devia estar posicionado o centro da rede (desprezando a resistência do ar)?

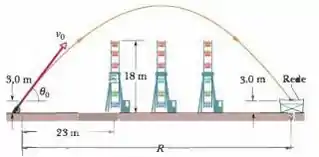
Dados : , distância entre a e a roda-gigante é .

Então galera, a boa desse exercício é achar a velocidade inicial e para isso vamos usar o fato de que Zacchini (tratado como um projétil) atinge a altura máxima ao passar pela roda do meio, situada no ponto situado a uma distância horizontal do ponto de lançamento, podemos calcular a velocidade escalar inicial usando a equação:

Dessa forma:

Com a velocidade escalar inicial podemos obter a altura vertical do projétil usando a fórmula:

Como a altura da roda-gigante é , ele passou a uma distância de:

Da primeira roda-gigante.