O ângulo de incidência , na Figura 33.59 é escolhido de modo que o raio luminoso passe simetricamente através do prisma, cujo indice de refração é e o ângulo do vértice é A. a) Mostre que o ângulo do desvio (o ângulo entre a direção do raio incidente e a direção do raio emergente) é dado por
(Quando o raio luminoso passa simetricamente, como indicado, o ângulo do desvio é mínino) b) Use o resultado do item (a) para determinar o ângulo do desvio para um raio luminoso que passa simetricamente através de um prisma com três ângulos iguais () e indice de refração . c) Um certo vidro possui indice de refração igual a para a luz vermelha () e para o violeta (). Sabendo que os raios dessas duas cores passam simetricamente como descrito no item (a) e considerando , calcule a diferença entre os dois ângulos dos desvios desses dois raios.
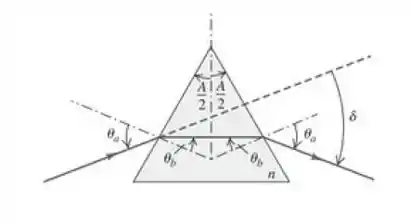
Passo 1
Aplicando a lei de snell na superficie do prisma:
Olhando para a figura, temos que o ângulo entre o segmento tracejado (raio emergente) e o raio refratado no prisma vale .
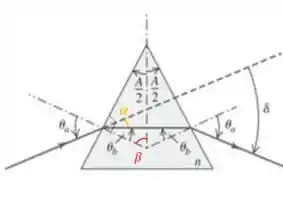
Olhando para o triângulo retângulo, temos que:
Então,
Agora, olhando para o outro triângulo retângulo, com os ângulo e , temos
Substituindo o valor de
Então, a lei de snell fica:
Vamos analisar agora o . Vimos que portanto
O ângulo é justamente o ângulo entre o raio incidente e o raio refratado.
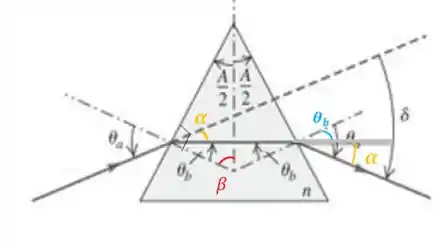
Conseguimos ver que:
Então:
Voltando na lei de snell:
Passo 2
b)
substituindo....
Resolvendo
Passo 3
c) vamos calcular o desvio de cada cor em relação ao raio incidente, e depois subtraímos um do outro, assim teremos o desvio relativo entre as duas cores.
Para o vermelho:
Para o violeta:
Então o desvio entre os dois é:
Resposta
a)
demonstração
b)
c)