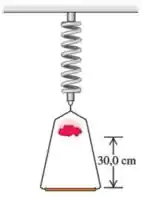
Uma armação de , quando suspensa por uma mola, estica essa mola em . Um pedaço de massa de parte do repouso sobre a armação de uma altura de (Figura PS.78). Determine a distância máxima que a armação se move a partir de sua posição de equilíbrio inicial.
Passo 1
E aí, galerinha! Qual a boa?

Uma armação de massa estica uma mola em repouso. Uma pequena massa parte do repouso a acima da armação e cai sobre ela, ficando sobre a armação.
Com isso, temos que determinar até quanto, em metros, a armação se afasta da posição de equilíbrio inicial (distância máxima adicional ).
Como vamos resolver isso?
Vamos dividir o problema em etapas: primeiro achamos a constante da mola usando o equilíbrio estático; depois calculamos a velocidade da massa antes do impacto;
Em seguida usamos conservação do momento para obter a velocidade do conjunto imediatamente após a colisão inelástica;
Por fim aplicamos conservação de energia
(cinética → energia elástica + variação potencial gravitacional)
Para achar o deslocamento máximo .
Lembrando que:
- Equilíbrio estático:
- Queda livre: velocidade ao atingir a armação
- Colisão perfeitamente inelástica (as massas ficam juntas): conservação do momento linear na colisão instantânea (forças externas desprezáveis durante o impacto):
- Energia cinética após a colisão:
Bora lá!
Passo 2
Primeiro, quando a armação de massa está suspensa em repouso, ela estica a mola uma distância . Nesse ponto a força elástica equilibra o peso, então aplicamos . Substituímos e para obter
Esse é o valor da constante elástica da mola que vamos usar adiante.
Agora pensamos na massa que parte do repouso a altura acima da armação.
Ao atingir a armação, sua velocidade é obtida pela conservação da energia durante a queda livre:
No impacto a massa fica sobre a armação . Assumimos colisão perfeitamente inelástica (elas movem-se juntas imediatamente após o choque). Durante o impacto, a duração é muito curta e, portanto, podemos usar a conservação do momento linear para determinar a velocidade combinada logo após a colisão. Assim,
A energia cinética do conjunto imediatamente após a colisão é
Podemos obter mais economicamente usando a expressão algébrica que elimina : com temos
Substituindo , , e :
Tranquilo até aqui?
Passo 3
Agora partimos da posição de equilíbrio inicial (aquela com só a armação) imediatamente após a colisão: o conjunto (massa ) possui energia cinética e a mola tem sua energia correspondente ao estado de equilíbrio, mas como vamos trabalhar com variações a partir da posição de equilíbrio, essas energias iniciais de referência se cancelam.
Quando o conjunto desce uma distância adicional a partir da posição de equilíbrio, a mola armazena energia adicional e a energia gravitacional total diminui por . Fazendo as contas com cuidado (e usando para simplificar) chegamos à equação de conservação de energia entre o instante logo após a colisão e o instante de máximo deslocamento:
Reorganizando para obter a forma padrão:
Essa equação quadrática em nos dá a distância máxima (tomamos a raiz positiva física).
Substituímos: , , e .
Assim a equação é
Resolvendo pela fórmula quadrática, o discriminante é
A raiz positiva é
Arredondando para três algarismos significativos, obtemos
Portanto, a distância máxima que a armação se move a partir de sua posição de equilíbrio inicial é aproximadamente .
E fim! Entendeu tudo? Responde Aí!